
3-4动能定理 第三章动量守恒定律和能量守恒定律 力的空间累积效应:F对F积累→W,动能定理. 功 力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积,(功是标量,过程量) dw F cosd=Fcos as d方 B dw=F.dr 0°≤0≤90°,dW>0 90°<0<180°,dW<0 0=90°F⊥drdW=0
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积 . (功是标量,过程量) 0 90 , dW 0 dW = F cos dr = F cosds 90 180 , dW 0 W F r d = d 一 功 力的空间累积效应: F r W ,动能定理. = 90 F ⊥ dr dW = 0 F r d Fi 1 dr i r d B * * i 1 A F1 对 积累

3-4动能定理 第三章动量守恒定律和能量守恒定律 ◆变力的功 dW=F.d方 F cos0 W="F.d=Fcosir >合力的功=分力的功的代数和 dr W=∫∑F·d萨=∑∫F·dF=∑W rF=Fi+Fj方+FE Ldr dxi +dyj+dzk W=∫Fdx+∫F,dy+∫Fdz W-W.+W.+W
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 = = B A B A W F dr F cosdr 合力的功 = 分力的功的代数和 = = = i i i Wi W F r F r d d W = F x + F y + F z x d y d z d W =W x +W y +W z Fcos A r B dr r r o 变力的功 W F r d = d r xi yj zk d = d + d + d F F i F j F k x y z = + +

3-4动能定理 第三章动量守恒定律和能量守恒定律 ◆功的大小与参照系有关 功的量纲和单位dimW=ML2T-21J=1N·m △W ◆ 平均功率P= △t △W dw 瞬时功率P=lim F. △t→0 △t dt P=Fvcos0 功率的单位(瓦特)1W=1J·s1 1kW=103W
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 功的大小与参照系有关 dim ML T 1J 1N m 2 2 = = − 功的量纲和单位 W t W P 平均功率 = 瞬时功率 v = = = → F t W t W P t d d lim 0 P = Fvcos 功率的单位 (瓦特) 1W =1Js −1 1kW =103W

3-4动能定理 第三章动量守恒定律和能量守恒定律 例1一质量为m的小球竖直落入水中,刚接触 水面时其速率为W,·设此球在水中所受的浮力与重力 相等,水的阻力为F=一b心,b为一常量.求阻力对 球作的功与时间的函数关系. 解如图建立坐标轴 w=jFd步=了-bodx=-j加 dxdt 即 W=-bjo'di 又由2-5节例5知 v=voe w=b.6ed业 00 W=(e 1-10 X
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 例 1 一质量为 m 的小球竖直落入水中, 刚接触 水面时其速率为 . 设此球在水中所受的浮力与重力 相等, 水的阻力为 , b 为一常量. 求阻力对 球作的功与时间的函数关系 . 0 v Fr = −bv 解 如图建立坐标轴 t t x W F r b x b d d d d d = = − v = − v 即 W b d t 2 = − v 又由 2 - 5 节例 5 知 t m b − = e 0 v v W b t t t m b − = − 0 2 0 e d 2 v (e 1) 2 1 2 2 = 0 − − t m b W mv 0 v x o

3-4动能定理 第三章动量守恒定律和能量守恒定律 二质点的动能定理 dv W=∫Fd=∫Fd=∫Fds F=m dt w-m0s=广mot 2 1 -m) 2 2 动能(状态函数) 1 Ek= 2 2m 动能定理 合外力对质点所作的功, 等于质点动能的增量 W=Ek-Ek 功和动能都与参考系有关;动能定理 仅适用于惯性系
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 二 质点的动能定理 2 1 2 2 2 1 2 1 d d d d 2 1 2 1 v v v v v v v v v s m m m t W = m = = − 动能(状态函数) m p E m 2 2 1 2 2 k = v = t F m d d t v W F dr F dr F ds = = t = t = 动能定理 W = Ek2 −Ek1 合外力对质点所作的功, 等于质点动能的增量 . 功和动能都与 参考系有关;动能定理 仅适用于惯性系 . 注意

3-4动能定理 第三章动量守恒定律和能量守恒定律 例2一质量为1.0kg的小球系在长为1.0m细绳下 端,绳的上端固定在天花板上.起初把绳子放在与竖直 线成30°角处,然后放手使小球沿圆弧下落.试求绳与 竖直线成10°角时小球的速率. 解dW=F.d=Fd+pd =P.ds=-mgldecoso =-mglsin 0do W =-mgl sin 0do =mgl(cos0-cosθ,)
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 P 例 2 一质量为1.0kg 的小球系在长为1.0m 细绳下 端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖直 线成 角处, 然后放手使小球沿圆弧下落 . 试求绳与 竖直线成 角时小球的速率 . 30 10 W F s F s P s d d d d T 解 = = + (cos cos ) = mgl − 0 = Pd s = −mgl d cos = −mglsin d = − 0 W mgl sin d d l 0 v FT s d
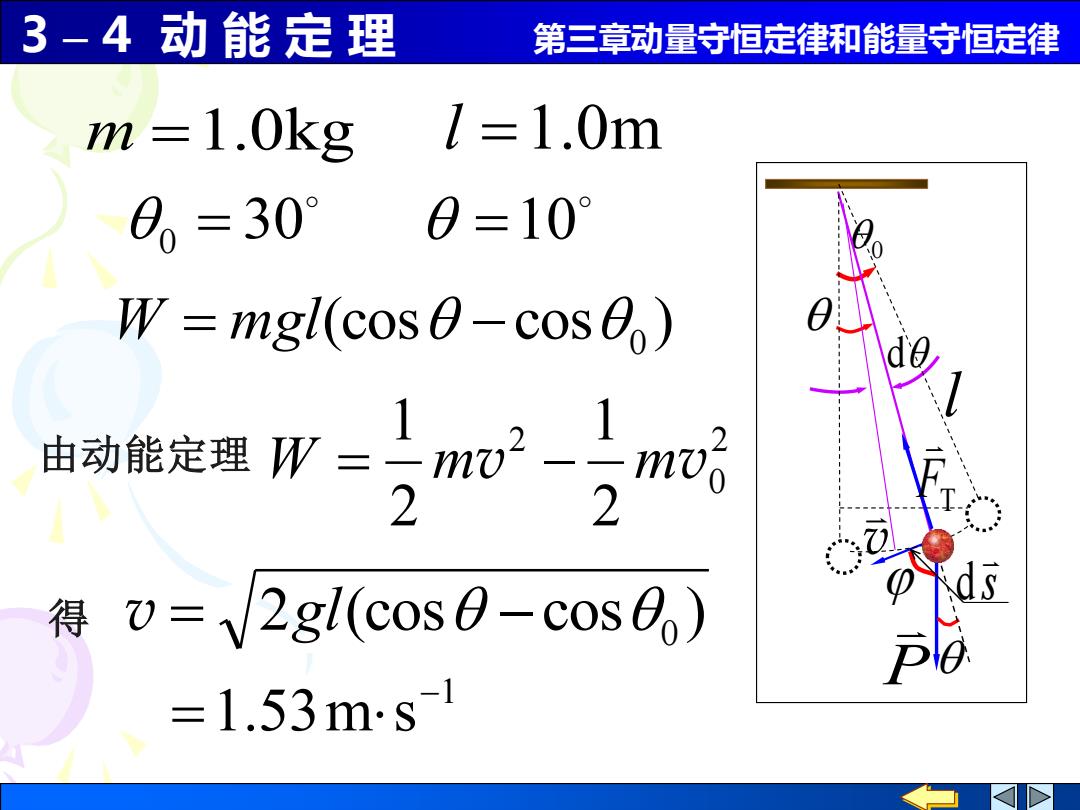
3-4动能定理 第三章动量守恒定律和能量守恒定律 m =1.0kg l=1.0m 0=30° 0=10° W =mgl(cos0-cos) 由动能定理W=m2-,m时 得v=V2gl(cos0-cos0,) =1.53ms1
3 – 4 动 能 定 理 第三章动量守恒定律和能量守恒定律 (cos cos ) W = mgl − 0 由动能定理 2 0 2 2 1 2 1 W = mv − mv 得 2 (cos cos ) v = gl − 0 1 1.53m s − = P d l 0 v FT s d m =1.0kg l =1.0m 0 = 30 =10