9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 fEds=1(g。-Q) 80 e-1 电容率£=E08, fE.as= EoEr 电位移矢量D=06E=E (均匀各相同性介质) 有介质时的高斯定理 fD.ds=∑2
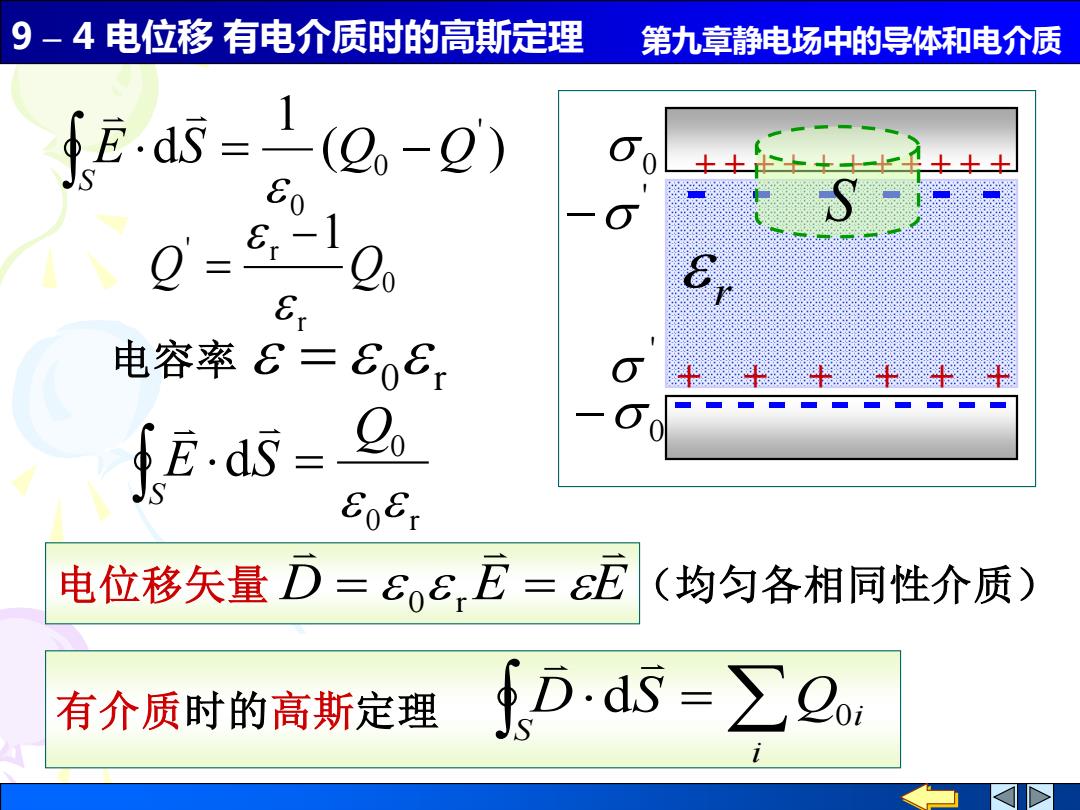
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 0 r ' r 1 Q Q − = ( ) 1 d ' 0 0 E S Q Q S = − D E E = = 电位移矢量 0 r (均匀各相同性介质) 0 − 0 ' − ' + + + + + + - - - - - - + + + + + + + + + + + - - - - - - - - - - - r S 电容率 0 r = 0 r 0 d Q E S S = 有介质时的高斯定理 = i i S D dS Q0

9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 D=P+5oE (任何介质) 电位移矢量 万=sE (均匀介质) 有介质时的高斯定理 fD.ds-∑2r 电容率 E=80E 极化电荷面密度 o'-P n C =6,C0 E=E/ (均匀介质) 有介质时先求D>E>U
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 极化电荷面密度 n ' = P C r C0 = 0 r E = E 电位移矢量 D P E 0 = + (任何介质) D E = (均匀介质) 有介质时的高斯定理 = i i S D dS Q0 电容率 0 r = (均匀介质) 有介质时先求 D → E →U 注意

9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 例1把一块相对电容率6=3的电介质,放在极 板间相距d=lm的平行平板电容器的两极板之间. 放入之前,两极板的电势差是1000/.试求两极板间 电介质内的电场强度E,电极化强度P,极板和电介 质的电荷面密度,电介质内的电位移D = 解 -i0o0V-m'=10V.m1=103kV:m d 10-3 E=Eo/e,=3.33×102kV.m P=(e-1)8E=5.89×106Cm2 00=6oE0=8.85×106Cm2 o'=P=5.89×10-6Cm2 D=6oeE=6E=o0=8.85×10-6Cm2
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 例1 把一块相对电容率 的电介质,放在极 板间相距 的平行平板电容器的两极板之间. 放入之前,两极板的电势差是 . 试求两极板间 电介质内的电场强度 , 电极化强度 , 极板和电介 质的电荷面密度, 电介质内的电位移 . r = 3 1000V E P D d =1mm 解 1 6 1 3 1 0 3 V m 10 V m 10 kV m 10 1000 − − − − = = = = d U E 2 1 3.33 10 kV m − = 6 2 ( r 1) 0 5.89 10 C m - P = − E = − 6 2 0 0 0 8.85 10 C m − − = E = 6 2 ' 5.89 10 C m − − = P = 6 2 0 r 0 0 0 8.85 10 C m - D = E = E = = − 0 r E = E

9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 例2一平行平板电容器充满两层厚度各为d,和d, 的电介质,它们的相对电容率分别为81和C2,极板 面积为S·求(1)电容器的电容;(2)当极板上的 自由电荷面密度的值为可,时,两介质分界面上的极化 电荷面密度 解(DfD.dS D 三O0 d D E 60 EoErl EoErl d D E2 60 8o82 E08r2
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 + + + + + + + + + + + - - - - - - - - - - - d1 2 d + 0 − 0 例2 一平行平板电容器充满两层厚度各为 和 的电介质,它们的相对电容率分别为 和 , 极板 面积为 . 求(1)电容器的电容;(2)当极板上的 自由电荷面密度的值为 时,两介质分界面上的极化 电荷面密度. d1 2 d r1 r2 S 0 - - - - - - + + + + + + ' −1 ' +1 + + + + + + - - - - - - ' + 2 ' − 2 S1 D dS 0 S1 S = D = 0 E1 E2 0 r1 0 0 r1 1 = = D E 0 r2 0 0 r2 2 = = D E 解(1)
9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 D E EoEr CoEr D 60 882 E82 U=∫E.d[=Ed+E,d -4+4 (2)0'=1-1 60 U Erdz 82d
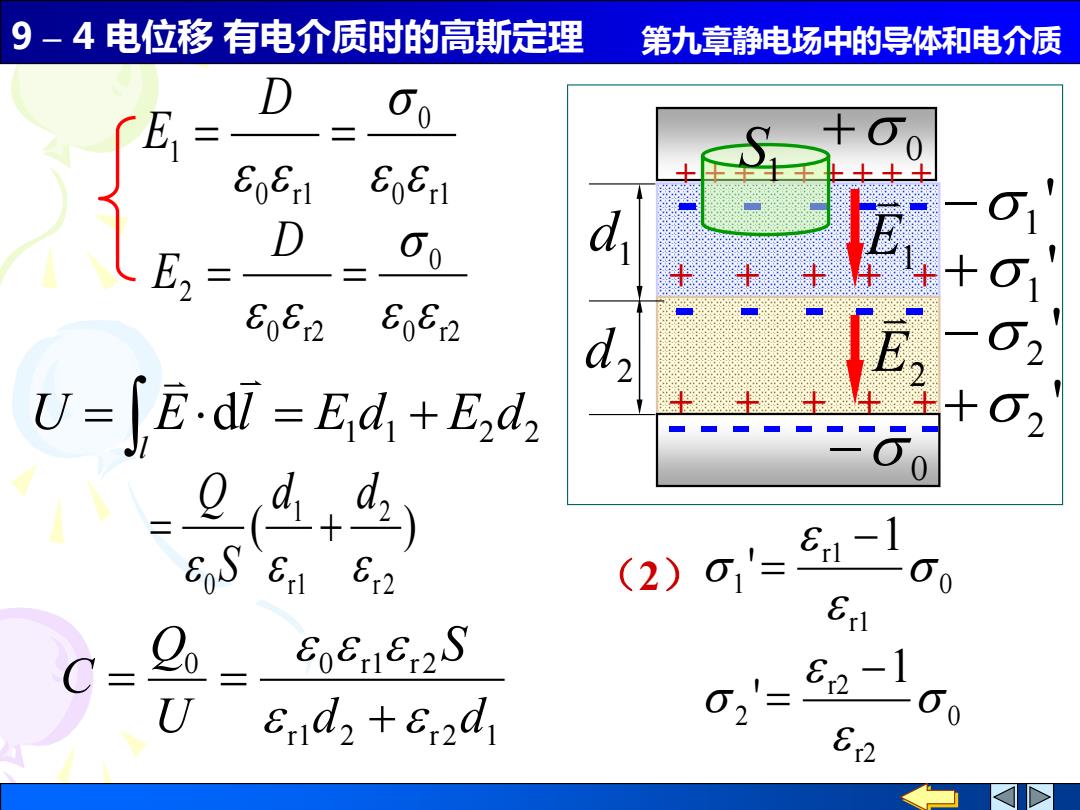
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 1 1 2 2 U E dl E d E d l = = + ( ) r2 2 r1 1 0 d d S Q = + r1 2 r2 1 0 0 r1 r2 d d S U Q C + = = 0 r1 r1 1 1 ' − = + + + + + - - - - - + + + + + + + + + - - - - - - - - - + + + + + - - - - - d1 2 d + 0 ' −1 ' +1 ' + 2 ' − 2 − 0 S1 E1 E2 0 r2 r2 2 1 ' − = (2) 0 r1 0 0 r1 1 = = D E 0 r2 0 0 r2 2 = = D E

9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 例3常用的圆柱形电容器,是由半径为R的长 直圆柱导体和同轴的半径为R的薄导体圆筒组成, 并在直导体与导体圆筒之间充以相对电容率为£,的 电介质.设直导体和圆筒单位长度上的电荷分别为+入 和一入·求(1)电介质中的电场强度、电位移和极 化强度;(2)电介质内、外表面的极化电荷面密度; (3)此圆柱形电容器的电容
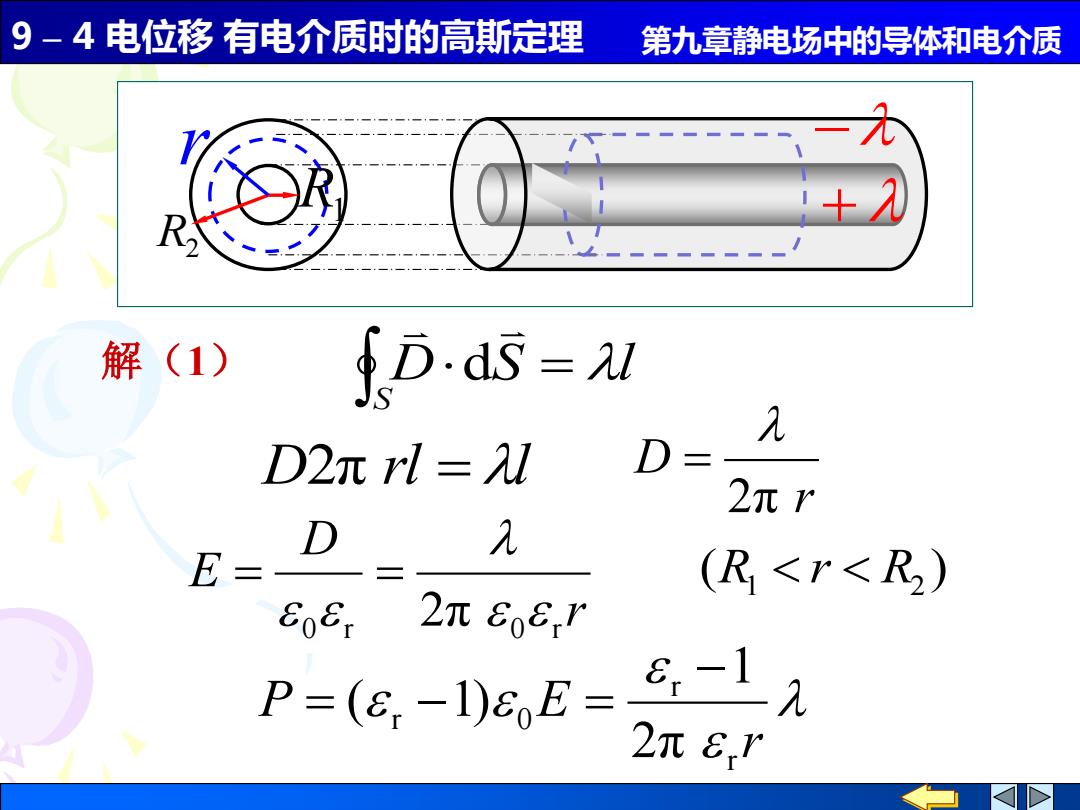
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 r 例3 常用的圆柱形电容器,是由半径为 的长 直圆柱导体和同轴的半径为 的薄导体圆筒组成, 并在直导体与导体圆筒之间充以相对电容率为 的 电介质.设直导体和圆筒单位长度上的电荷分别为 和 . 求(1)电介质中的电场强度、电位移和极 化强度;(2)电介质内、外表面的极化电荷面密度; (3)此圆柱形电容器的电容. + R1 R2 r − R1 R2 + −
9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 解(1) D.dsu D2πrl=21 D= 2元r D λ E- (R<r<R2) EoEr 2元80E,r P=(G,-18,E=9-1入 2元8r
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 D S l S = 解(1) d D2π rl = l r D 2π = r D E 0 r 2π 0 r = = ( ) 1 R2 R r r P E r r r 0 2π 1 ( 1) − = − = R1 R2 r + −
9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 (2)由上题可知 λ 2π6oGR (r=R) D E-=- 入 2元8oE1' (r=R2) EoE 2元6o6,R2 G=(G,-1cE,=(&,-02元eR o,=(e,-1)6E,=(&,-102e,R 入
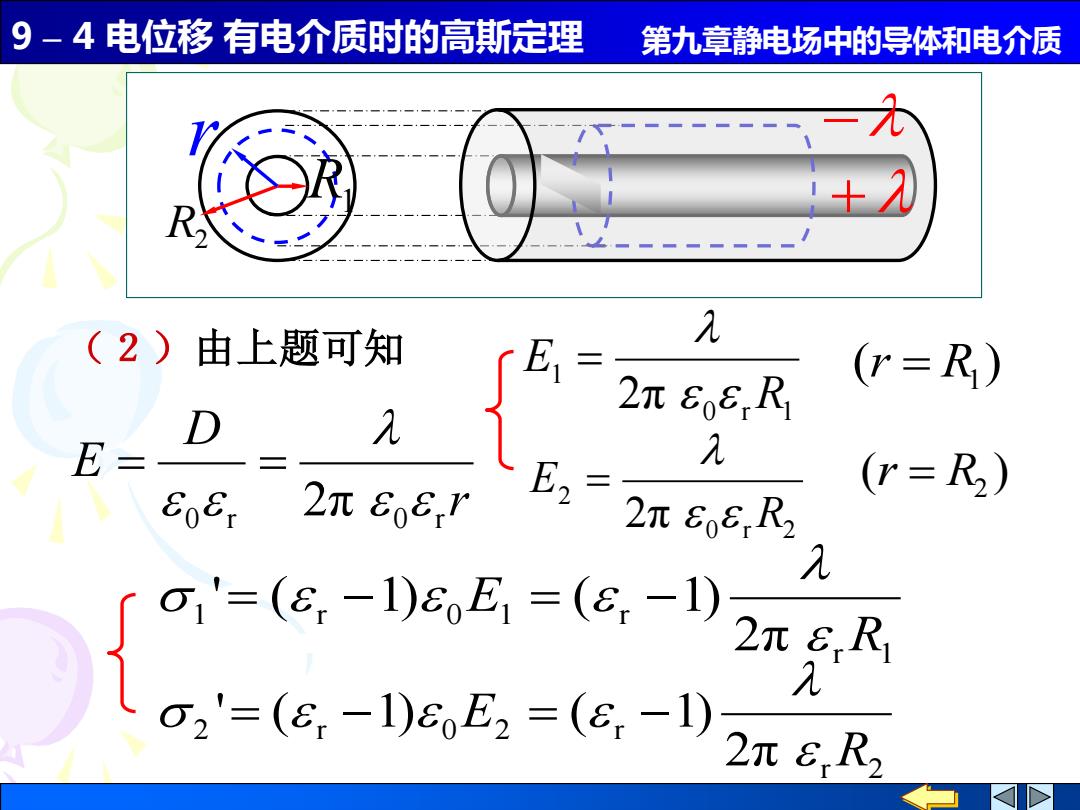
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 (2)由上题可知 r 1 1 r 0 1 r 2π ' ( 1) ( 1) R E = − = − r 2 2 r 0 2 r 2π ' ( 1) ( 1) R E = − = − 0 r 1 1 2π R E = ( ) R1 r = 0 r 2 2 2π R E = ( ) R2 r = r D E 0 r 2π 0 r = = R1 R2 r + −
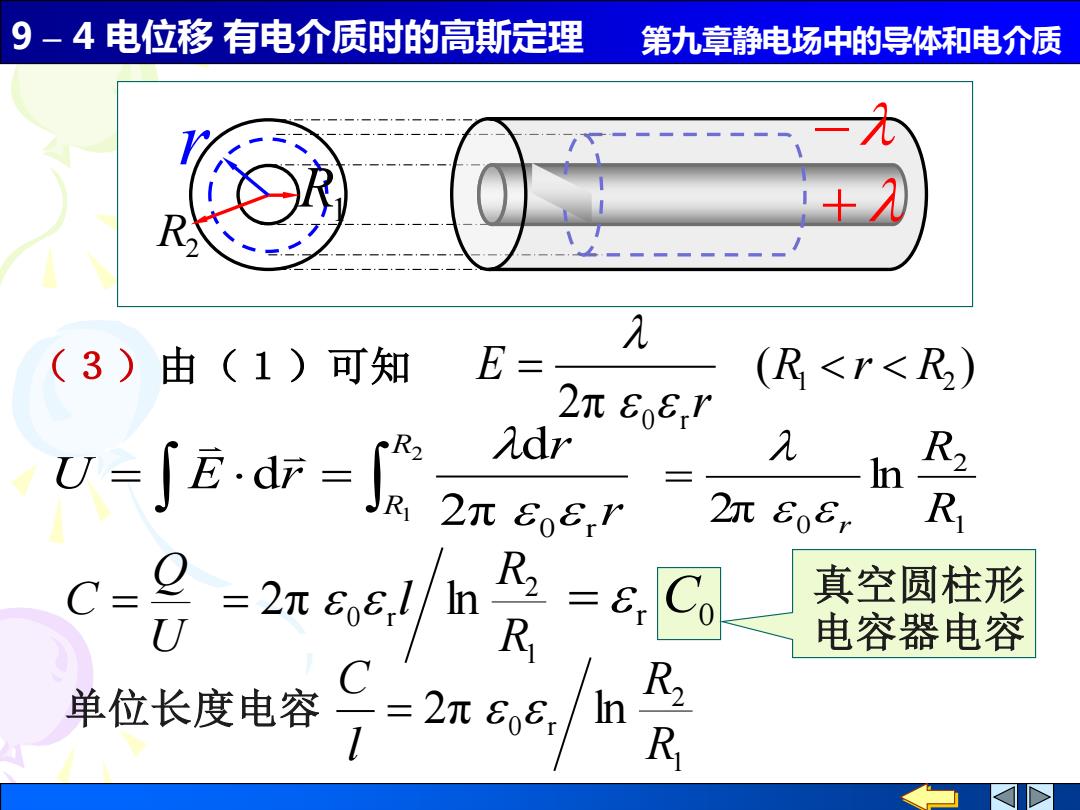
9-4电位移有电介质时的高斯定理 第九章静电场中的导体和电介质 2 (3)由(1)可知 E- (R<r<R) 2元681 u-Rd-2 λdr R2 三 2元E08r R R2二8x 真空圆柱形 电容器电容 单位长度电容 C=2806 R2 R
9 – 4 电位移 有电介质时的高斯定理 第九章静电场中的导体和电介质 真空圆柱形 电容器电容 (3)由(1)可知 r E 0 r 2π = ( ) 1 R2 R r = = 2 1 2π 0 r d d R R r r U E r 1 2 0 ln 2π R R r = 1 2 0 r 2π ln R R = l U Q C = r C0 = 1 2 0 r 2π ln R R l C 单位长度电容 = R1 R2 r + −