
14-1简谐运动 第十四章机械振动 任一物理量在某一定值附近往复变化均称为振动. 机械振动物体围绕一固定位置往复运动. 其运动形式有直线、平面和空间振动. 例如一切发声体、心脏、海浪起伏、地震以及晶体 中原子的振动等 周期和非周期振动 简谐运动 最简单、最基本的振动 合成 简谐运动 复杂振动 分解 谐振子 作简谐运动的物体
14 – 1 简谐运动 第十四章 机械振动 任一物理量在某一定值附近往复变化均称为振动. 机械振动 物体围绕一固定位置往复运动. 其运动形式有直线、平面和空间振动. 周期和非周期振动 简谐运动 最简单、最基本的振动. 谐振子 作简谐运动的物体. 例如一切发声体、心脏、海浪起伏、地震以及晶体 中原子的振动等. 简谐运动 复杂振动 合成 分解
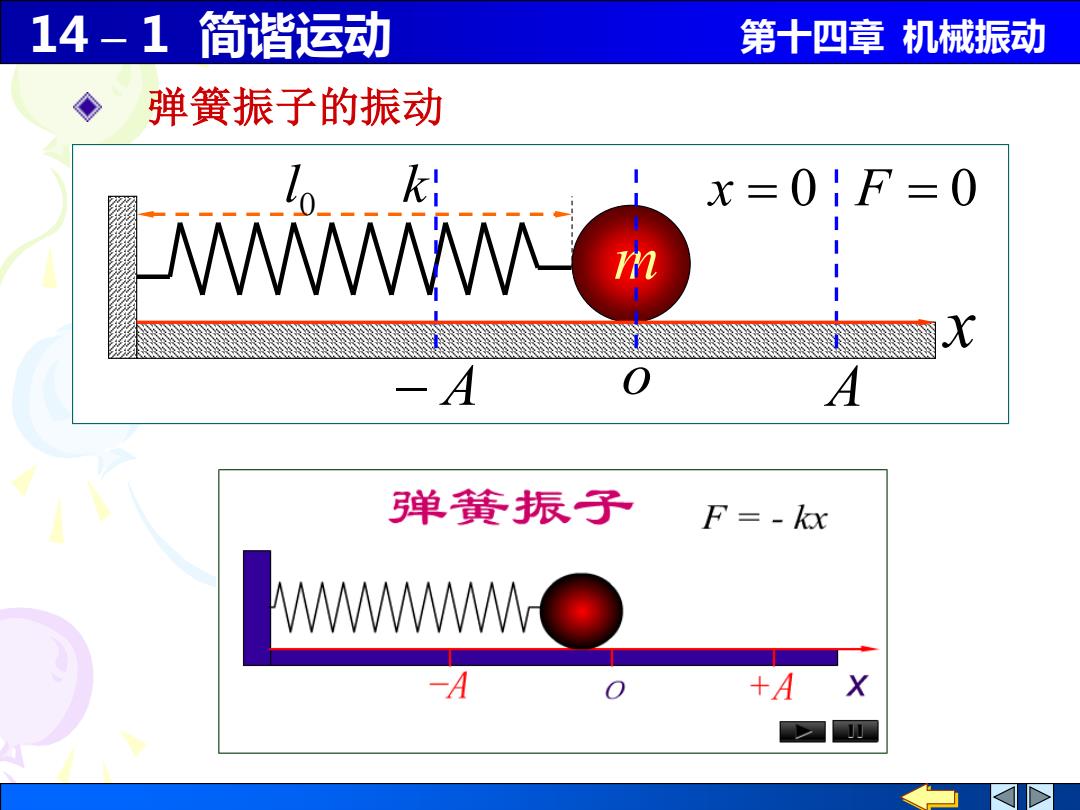
14-1简谐运动 第十四章机械振动 弹簧振子的振动 lo ki x=0!F=0 WWWM -A A 弹簧振子 F=-kx WWWWMO +A
14 – 1 简谐运动 第十四章 机械振动 l k 0 x m − A o A 弹簧振子的振动 x = 0 F = 0

14-1简谐运动 第十四章机械振动 F=-kx=ma x=Acos(or +o) 令02 k 积分常数,根据初始条件确定 m dx )= dt .=-Aosin(ot+p) d2x a= dt2 =-Aa2cos(@I+)
14 – 1 简谐运动 第十四章 机械振动 F = −kx = max t x 2 2 2 d d = − m k = 2 令 a x 2 = − sin( ) d d = = −A t + t x v cos( ) d d 2 2 2 = = −A t + t x a 积分常数,根据初始条件确定 x = Acos(t +) x x F m o
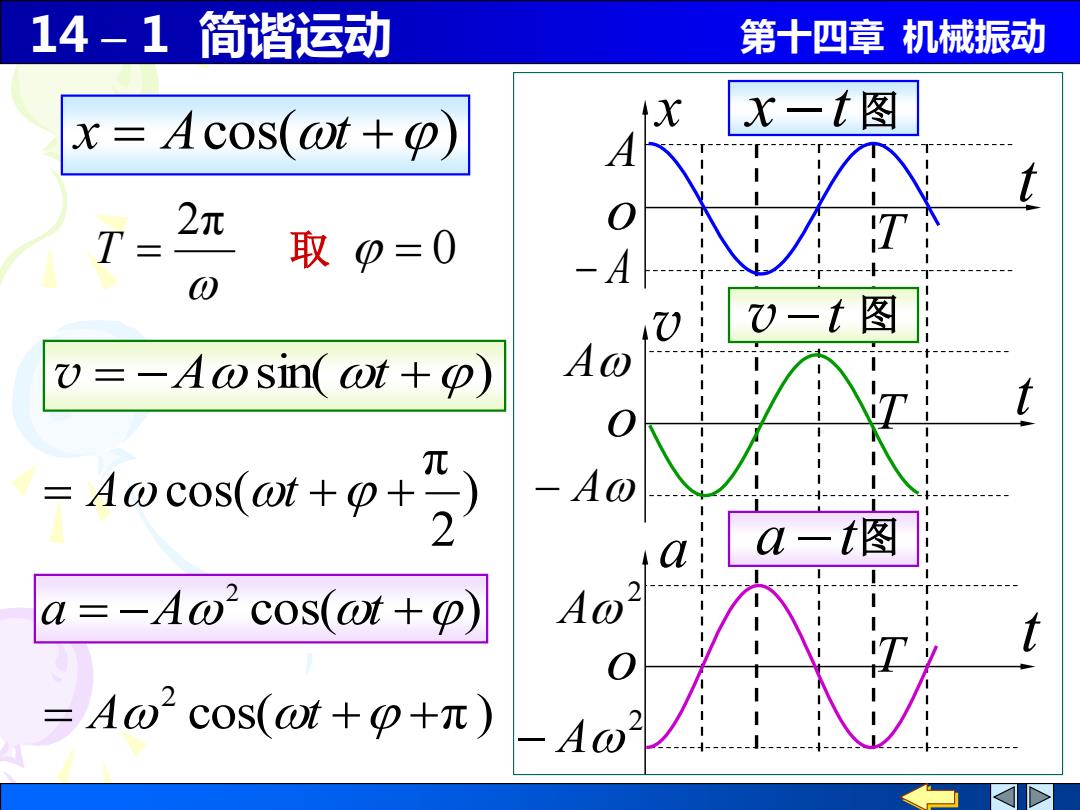
14-1简谐运动 第十四章机械振动 x=Acos(at+) x一t图 T- 2元 取0=0 ⊙ 71 )-t图日 =-A0sin(ot+o) =A0cos(o+0+)】 -A0 a-t图 a=-A@'cos(at+p) A@ =A@'cos(ot+p+元)
14 – 1 简谐运动 第十四章 机械振动 x −t 图 v −t 图 a −t 图 T A − A 2 A 2 − A x v a t t t A − A o o o T T x = Acos(t +) 取 = 0 2π T = ) 2 π = A cos(t + + v = −A sin(t +) cos( π ) 2 = A t + + cos( ) 2 a = −A t +