
14-7阻尼振动 受迫振动共振 第十四章机械振动 阻尼振动 阻力系数 阻尼力 F=-C) -kx-Co=ma dx m dt2 +C +kx=0 00= 固有角频率 dt m d2x dx +26 +06x=0 δ=C/2m 阻尼系数 dt X= Ae cos(ot+p) 振幅 角频率 2π T-2= 2元 0-2 2 ⊙
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 振幅 角频率 −kx−Cv = ma 0 d d d d 2 2 + + k x = t x C t x m 0 d d 2 d d 2 2 0 2 + + x = t x t x 一 阻尼振动 cos( ) = + − x Ae t t 2 2 = 0 − 2 2 0 2π 2π T = = − 阻尼力 Fr = −Cv m k 0 = = C 2m 固有角频率 阻尼系数 阻力系数
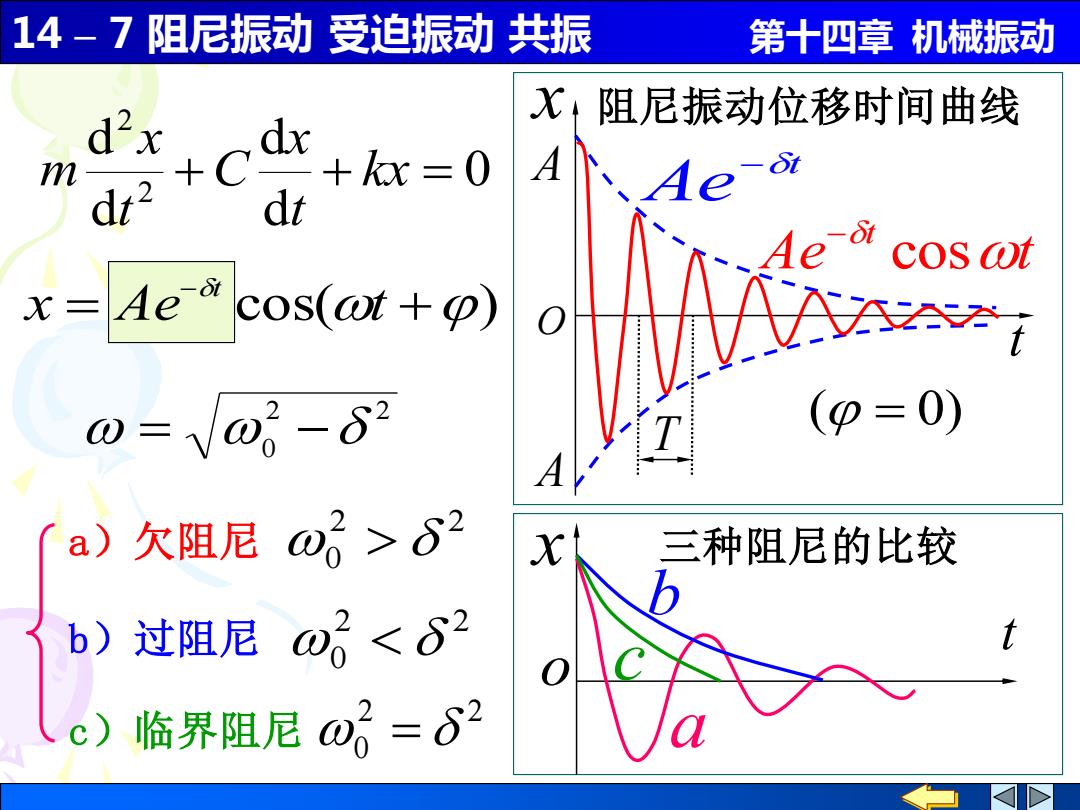
14-7阻尼振动受迫振动共振 第十四章机械振动 d2x X:阻尼振动位移时间曲线 m dt2 +x=0 dt Ae-3 Ae cos wt x-Ae cos(at +p) @=@j-82 a)欠阻尼 o>62 三种阻尼的比较 b)过阻尼 ω<δ2 临界阻尼@=62
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 o t x 三种阻尼的比较 阻尼振动位移时间曲线 A A t O x 2 2 ( = 0) = 0 − cos( ) = + − x Ae t t 0 d d d d 2 2 + + kx = t x C t x m 2 2 b)过阻尼 0 2 2 a)欠阻尼 0 2 2 c)临界阻尼 0 = t Ae− T a b c Ae t t cos −

14-7阻尼振动受迫振动共振 第十四章机械振动 例有一单摆在空气(室温为20°C)中来回摆动 其摆线长1=1.0m,摆锤是一半径r=5.0×103m 的铅球.求(1)摆动周期;(2)振幅减小10%所需的 时间;(3)能量减小10%所需的时间;(4)从以上所 得结果说明空气的粘性对单摆周期、振幅和能量的影响 (已知铅球密度为p=2.65×10kg·m3,20°C 时空气的粘度7=1.78×105Pa·s) 解(1)@=Vg/1=3.13s F=-6mr70=-C) 6=C/2m=9n/4r2p=6.04×104s1 2元 2元 .:δ<<00 ∴.T= ≈2s vo-82 00
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 例 有一单摆在空气(室温为 )中来回摆动. 其摆线长 ,摆锤是一半径 的铅球. 求(1)摆动周期;(2)振幅减小10%所需的 时间;(3)能量减小10%所需的时间;(4)从以上所 得结果说明空气的粘性对单摆周期、振幅和能量的影响. 20 C l =1.0m 5.0 10 m −3 r = (已知铅球密度为 , 时空气的粘度 ) 3 3 2.65 10 kg m − = 20 C 1.78 10 Pa s 5 = − 解 (1) 1 0 3.13s − = g l = Fr = −6π rv = −Cv 2 4 1 2 9 4 6.04 10 s − − = C m = r = 0 2s 2π 2π 0 2 2 0 − = T

14-7阻尼振动受迫振动共振 第十四章机械振动 (2) 有阻尼时A'三= e-a 0.9A= Ae -δt1 n 1 t1= 0.9 6 =174s≈3min (3) E e-20 E 0.9 三 e-2672 0. t2= 2=87s≈1.5min 2δ
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 (2) 有阻尼时 t A A − ' = e 1 0.9 e t A A − = 174s 3min 0.9 ln 1 1 = = t (3) t A A E E 2 2 ) e ' ( ' − = = 2 2 0.9 e − t = 87s 1.5min 2 0.9 ln 1 2 = = t

14-7阻尼振动受迫振动共振 第十四章机械振动 二 受迫振动 k d2x + dx m dt2 dt xFcoS@pt 2δ=C/m 驱动力 d2x +28x=fcos@ dx 、f=F/m dt 驱动力的角频率 x=Ae cos(at+p)+Acos(@t+y) -2δ A- 0 tgy=- V(o6-o)+4620g 2 2 Q
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 驱动力 kx F t t x C t x m 2 p 2 cos d d d d + + = 二 受迫振动 m k 0 = 2 = C m f = F m x f t t x t x p 2 2 0 2 cos d d 2 d d + + = cos( ) cos( ) 0 p = + + + − x A e t A t t 2 p 2 2 p 2 0 ( − ) + 4 = f A 2 p 2 0 2 p − − t g = 驱动力的角频率
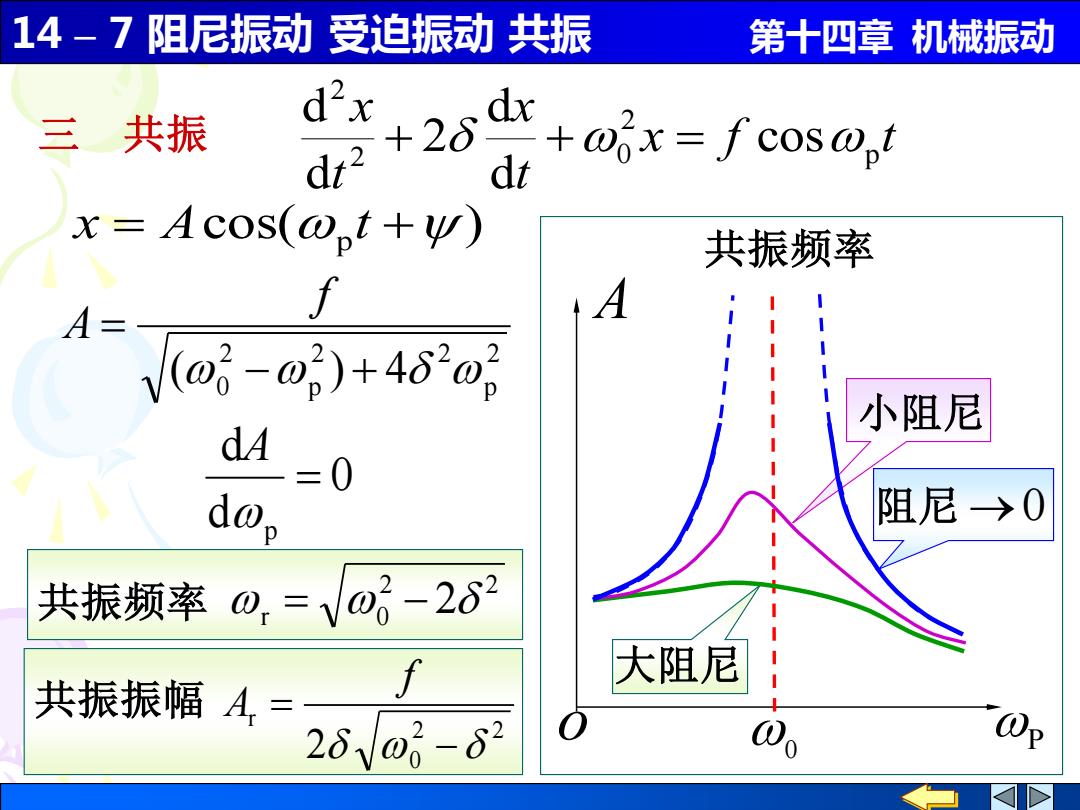
14-7阻尼振动受迫振动共振 第十四章机械振动 dx 三共振 dx+2 dt2 x=fcos@t dt x=Acos(o,t+Ψ) 共振频率 A A= V(o-@)+482o 小阻尼 d 1=0 d@p 阻尼→0 共振频率0,=√@-262 大阻尼 共振振幅A= 26V-82
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 P A o 共振频率 cos( ) x = A p t + 2 p 2 2 p 2 0 ( − ) + 4 = f A 0 大阻尼 小阻尼 2 2 r 0 共振频率 = − 2 2 2 0 r 2 − = f 共振振幅 A 0 d d p = A 阻尼 →0 三 共振 x f t t x t x p 2 2 0 2 cos d d 2 d d + + =

14-7阻尼振动受迫振动共振 第十四章机械振动 共振频率 共振演示实验 0,=Vo-282 共振振幅 26Vo-62 2 单摆1作垂直于纸面 共振现象在实际中的应用 的简谐运动时,单摆5将 作相同周期的简谐运动, 乐器、收音机… 其它单摆基本不动
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 共振演示实验 2 3 6 1 4 5 2 2 r 0 = − 2 共振频率 2 2 0 r 2 − = f A 共振振幅 共振现象在实际中的应用 乐器、收音机 …… 单摆1作垂直于纸面 的简谐运动时,单摆5将 作相同周期的简谐运动, 其它单摆基本不动

14-7阻尼振动受迫振动共振 第十四章机械振动 >共振现象的危害 1940年7月1日美国Tocama悬索桥因共振而坍塌
14 – 7 阻尼振动 受迫振动 共振 第十四章 机械振动 共振现象的危害 1940 年7月1日美国 Tocama 悬索桥因共振而坍塌