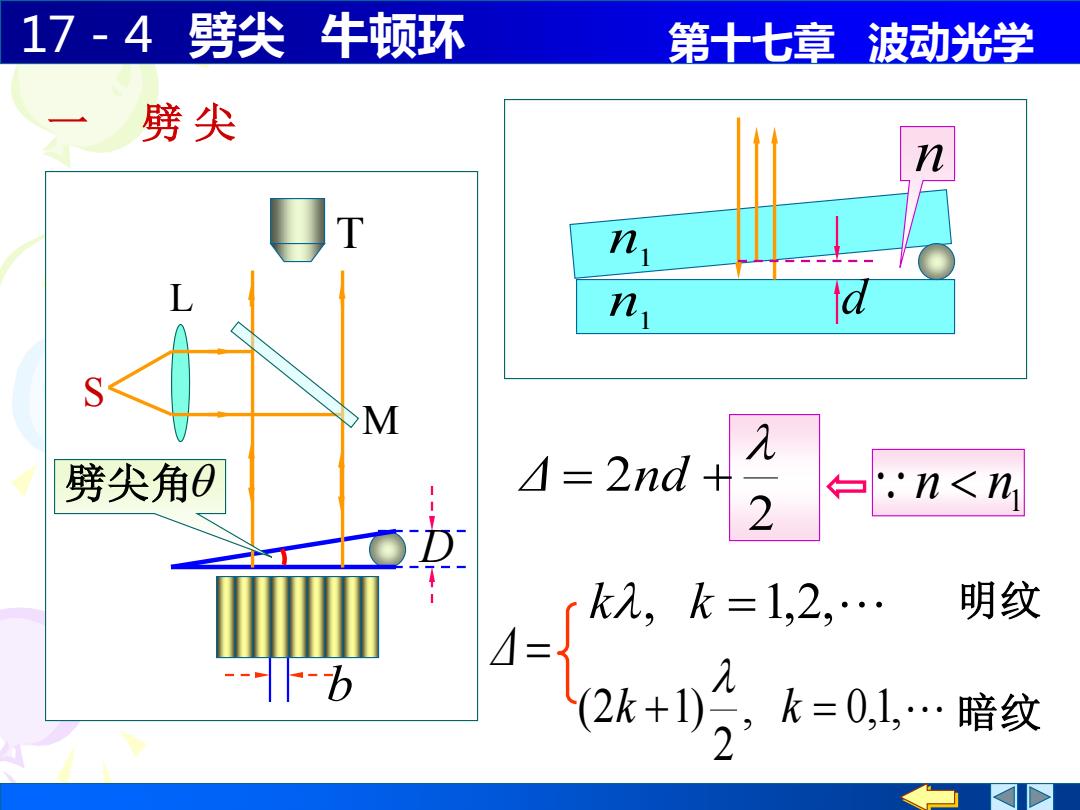
17-4劈尖 牛顿环 第十七章波动光学 劈尖 n T n n a M 劈尖角0 /=2nd 2 .'n<n k2,k=1,2,… 明纹 = b 2k+分k=0L…暗纹
17-4 劈尖 牛顿环 第十七章 波动光学 n1 n1 n S M D T L 劈尖角 1 n n 一 劈 尖 2 2 Δ = nd + Δ = k, k =1,2, 明纹 , 0,1, 2 (2k +1) k = 暗纹 b d
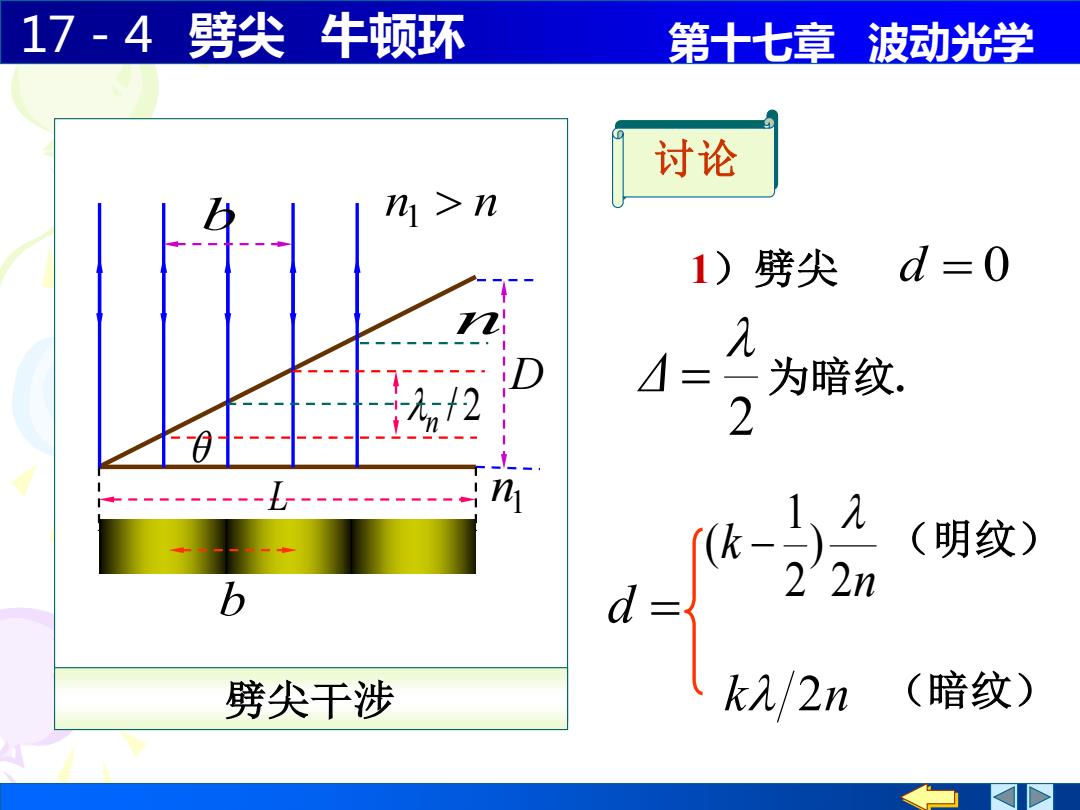
17-4劈尖 牛顿环 第十七章波动光学 讨论 n>n 1)劈尖 d=0 人= 为暗纹、 2 1、 (明纹) 2n 劈尖干涉 k/2n (暗纹)
17-4 劈尖 牛顿环 第十七章 波动光学 L n 1 n D 劈尖干涉 n1 n d = n k 2 ) 2 1 ( − k 2n (明纹) (暗纹) b b / 2 n 讨论 1)劈尖 2 Δ = d = 0 为暗纹
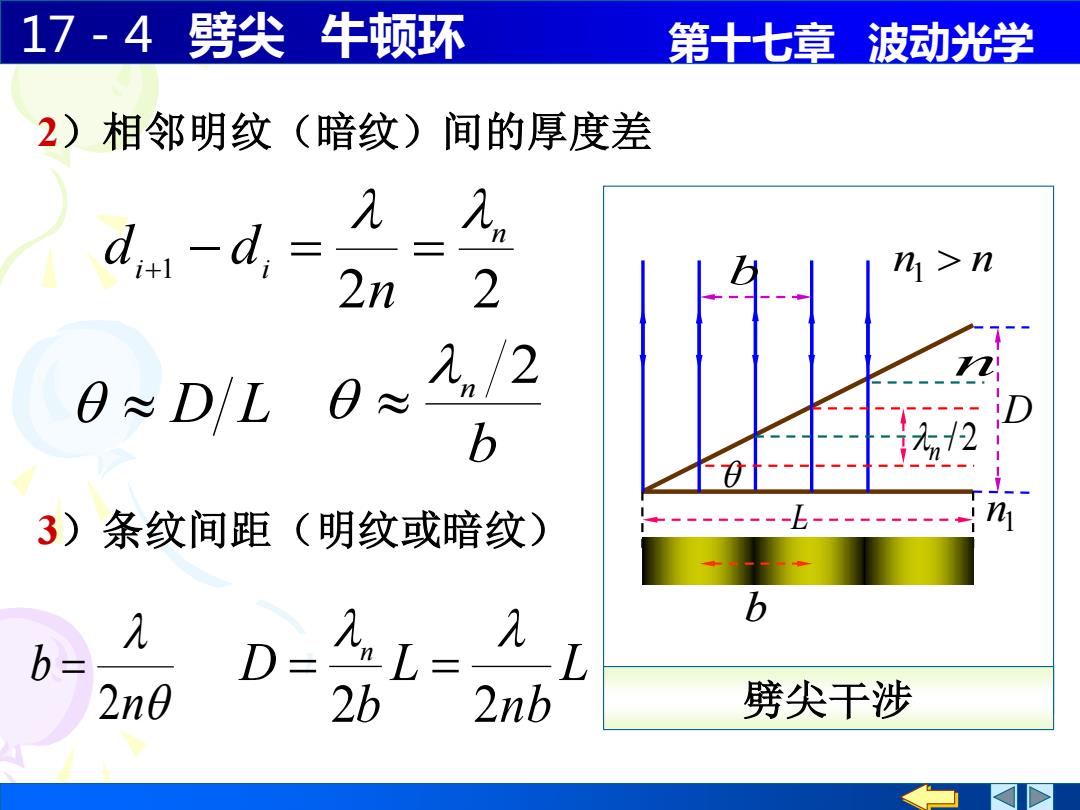
17-4劈尖牛顿环 第十七章波动光学 2)相邻明纹(暗纹)间的厚度差 d1-d,= n>n 2n 2 九./2 0≈D/L0≈ b 无2 3)条纹间距(明纹或暗纹) b= D AL= 2n0 2b nb 劈尖干涉
17-4 劈尖 牛顿环 第十七章 波动光学 L nb L b D n 2 2 = = 3)条纹间距(明纹或暗纹) n b 2 = 2 2 1 n i i n d d + − = = 2)相邻明纹(暗纹)间的厚度差 D L b n 2 L n 1 n D 劈尖干涉 n1 n / 2 n b b
17-4劈尖 牛顿环 第十七章波动光学 4)干涉条纹的移动 每一条 纹对应劈尖 内的一个厚 度,当此厚 度位置改变 时,对应的 条纹随之移 动. 转动 平移 复位
17-4 劈尖 牛顿环 第十七章 波动光学 每一条 纹对应劈尖 内的一个厚 度,当此厚 度位置改变 时,对应的 条纹随之移 动. 4 )干涉条纹的移动
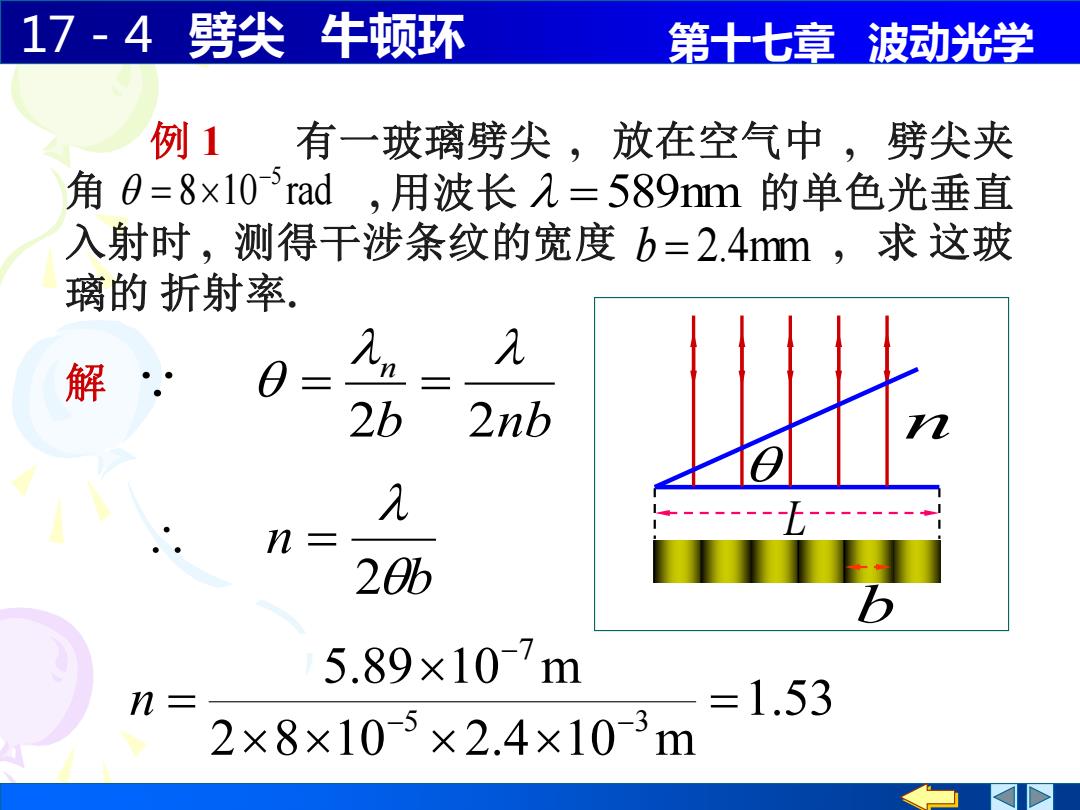
17-4劈尖牛顿环 第十七章波动光学 例1有一玻璃劈尖, 放在空气中,劈尖夹 角0=8×105rad,用波长入=589nm 的单色光垂直 入射时,测得干涉条纹的宽度b=2.4m,求这玻 璃的折射率。 几 解 2b 2nb 元 n 20b 5.89×10-7m n= =1.53 2×8×105×2.4×103m
17-4 劈尖 牛顿环 第十七章 波动光学 L n b 例 1 有一玻璃劈尖 , 放在空气中 , 劈尖夹 角 8 10 rad −5 = , 用波长 的单色光垂直 入射时 , 测得干涉条纹的宽度 , 求 这玻 璃的 折射率. = 589nm b = 2.4mm 解 b nb n 2 2 = = 1.53 2 8 10 2.4 10 m 5.89 10 m 5 3 7 = = − − − n b n 2 =
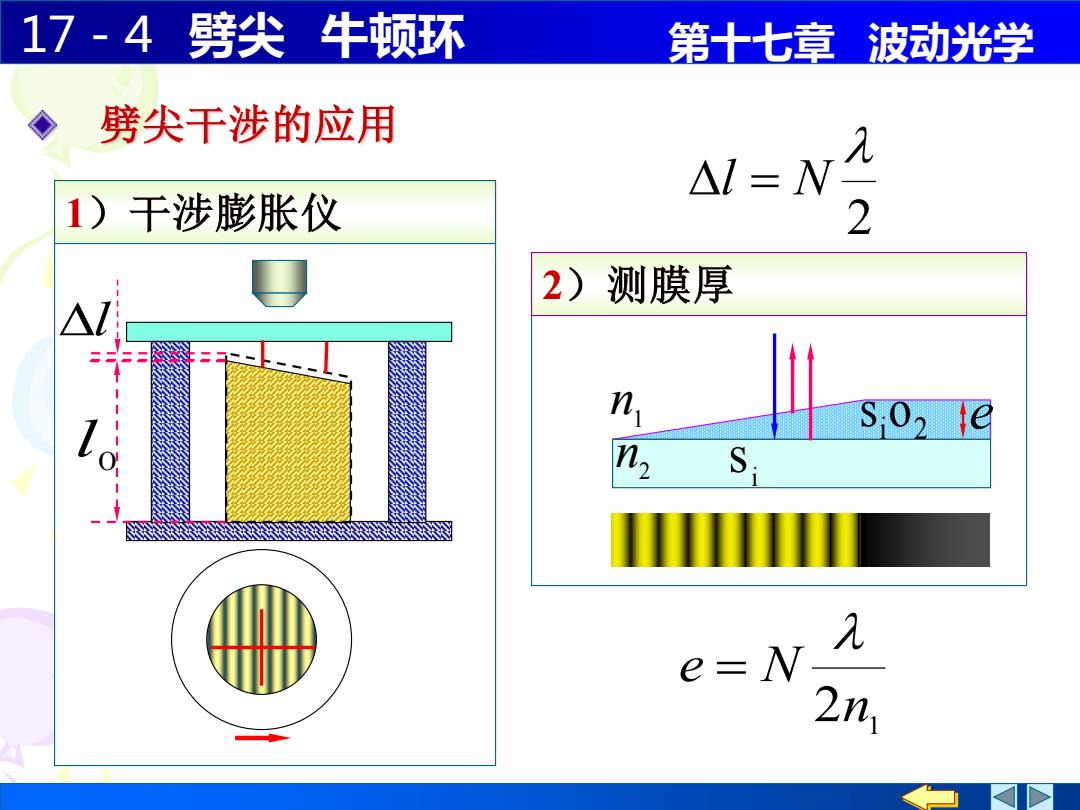
17-4劈尖牛顿环 第十七章波动光学 劈尖干涉的应用 △l=N 1)干涉膨胀仪 2 2)测膜厚 n s:0,ie n, S e =N 2n
17-4 劈尖 牛顿环 第十七章 波动光学 2)测膜厚 i s 1 e n 2 n i 2 s o 1)干涉膨胀仪 0 l 劈尖干涉的应用 2n1 e N = l 2 l = N
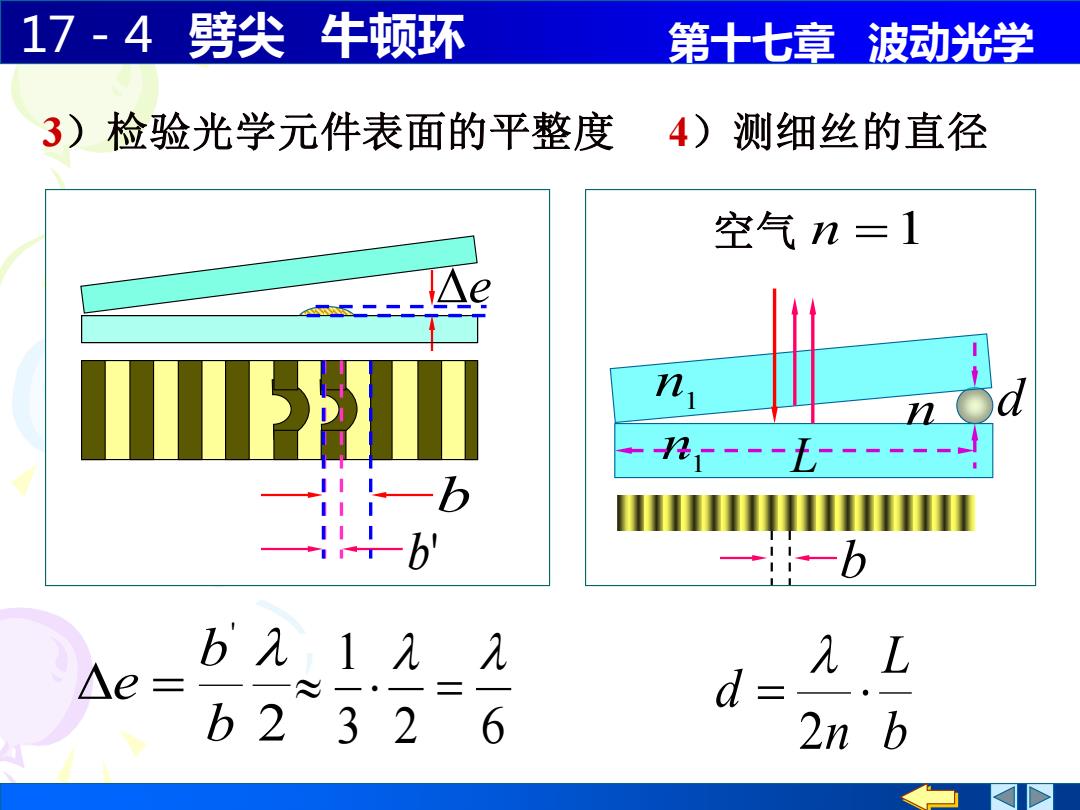
17-4劈尖牛顿环 第十七章波动光学 3)检验光学元件表面的平整度 4)测细丝的直径 空气n=1 n b21 ,见 元L △e= - b2326 d= 2n b
17-4 劈尖 牛顿环 第十七章 波动光学 n1 n n1 L d 空气 n =1 e 3)检验光学元件表面的平整度 2 ' b b e = 3 2 6 1 = b b' 4)测细丝的直径 b L n d = 2 b
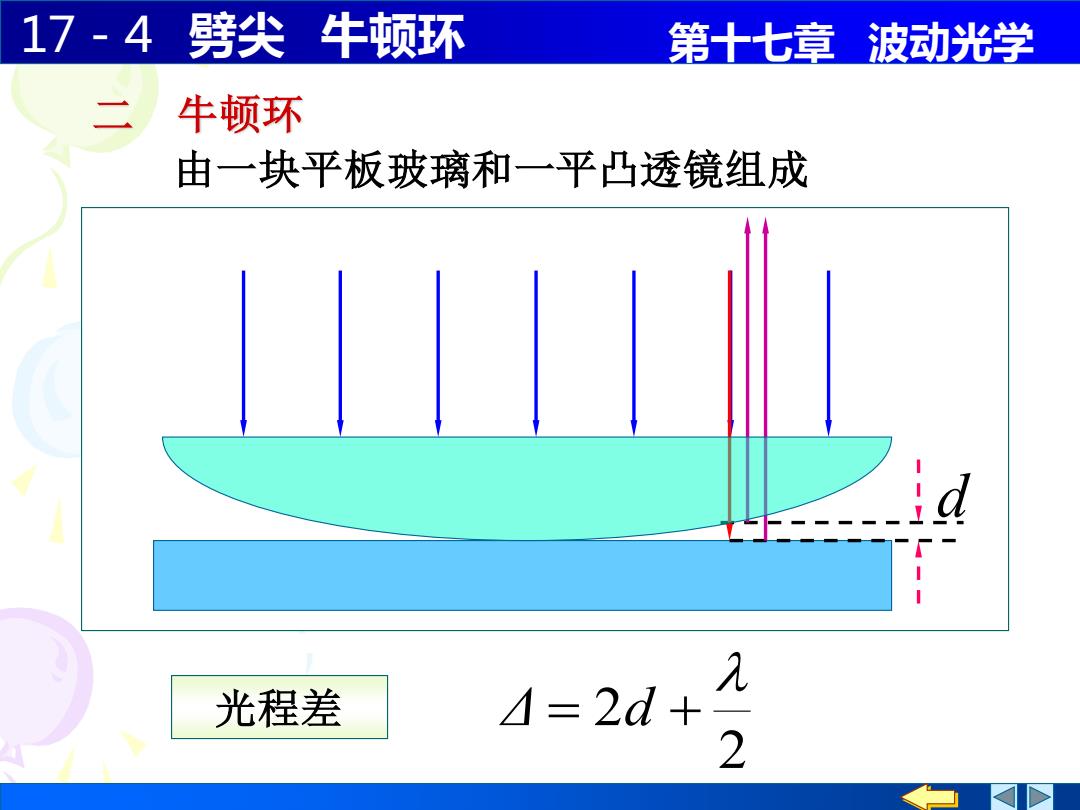
17-4劈尖 牛顿环 第十七章波动光学 二 牛顿环 由一块平板玻璃和一平凸透镜组成 d 光程差 /=2d+ 2
17-4 劈尖 牛顿环 第十七章 波动光学 d 二 牛顿环 由一块平板玻璃和一平凸透镜组成 2 2 光程差 Δ = d +
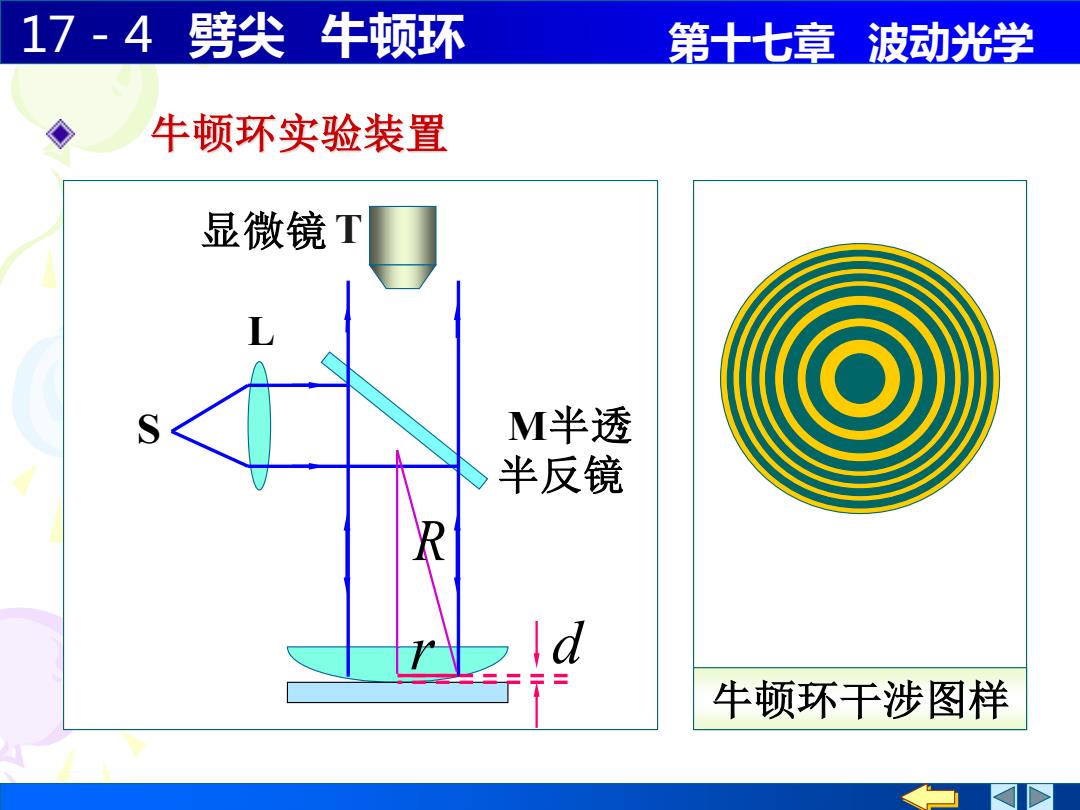
17-4劈尖牛顿环 第十七章波动光学 牛顿环实验装置 显微镜T M半透 半反镜 牛顿环干涉图样
17-4 劈尖 牛顿环 第十七章 波动光学 牛顿环实验装置 牛顿环干涉图样 显微镜 S L R r d M半透 半反镜 T
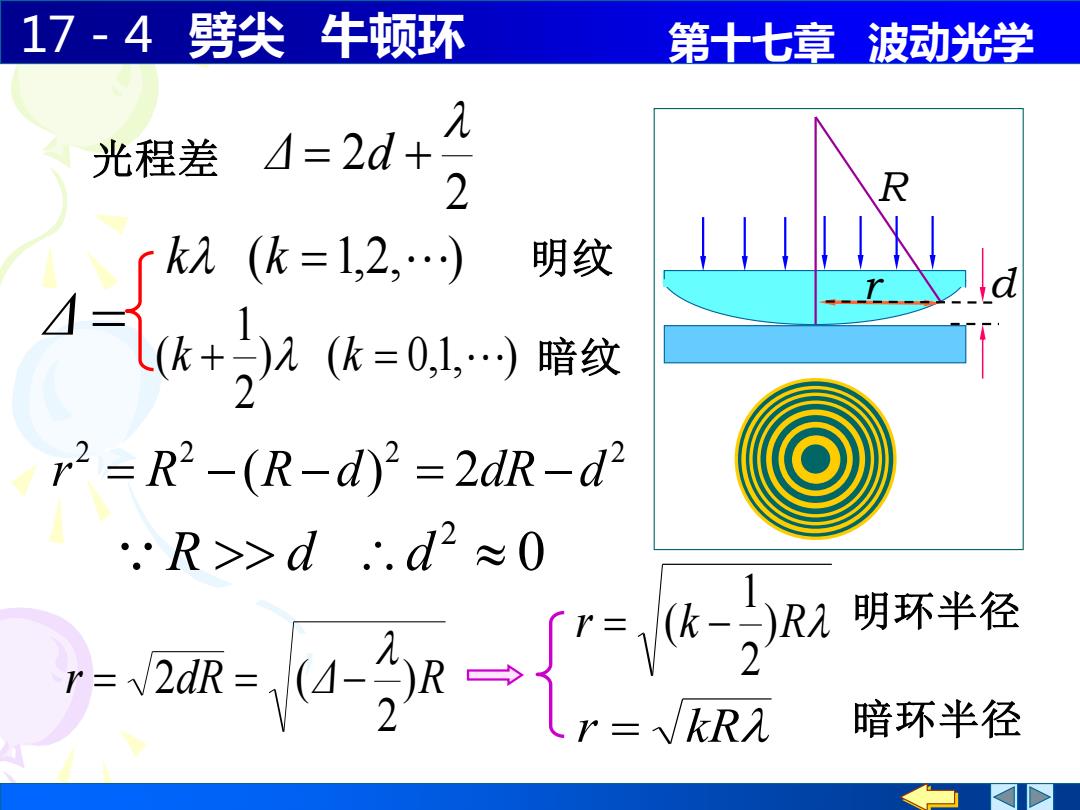
17-4劈尖 牛顿环 第十七章波动光学 光程差 1=2d+ 2 R k2(k=1,2,…) 明纹 d 1气+1《=01.)暗纹 2=R2-(R-d)2=2dR-d2 R>d.d2≈0 系 暗环半径
17-4 劈尖 牛顿环 第十七章 波动光学 R 2 2 2 2 r = R −(R − d) = 2dR − d 0 2 R d d r dR Δ )R 2 2 ( = = − 2 2 光程差 Δ = d + Δ = k (k =1,2, ) 明纹 ) ( 0,1, ) 2 1 (k + k = 暗纹 r d r k )R 2 1 = ( − r = kR 暗环半径 明环半径