18-6相对论性动量和能量 第十八章相对论 牛顿定律与光速极限的矛盾 物体在恒力作用下的运动 d啦 d(mò) dt dr F 00 a t m 经典力学中物体的质量与运动无关 V:=70 +at
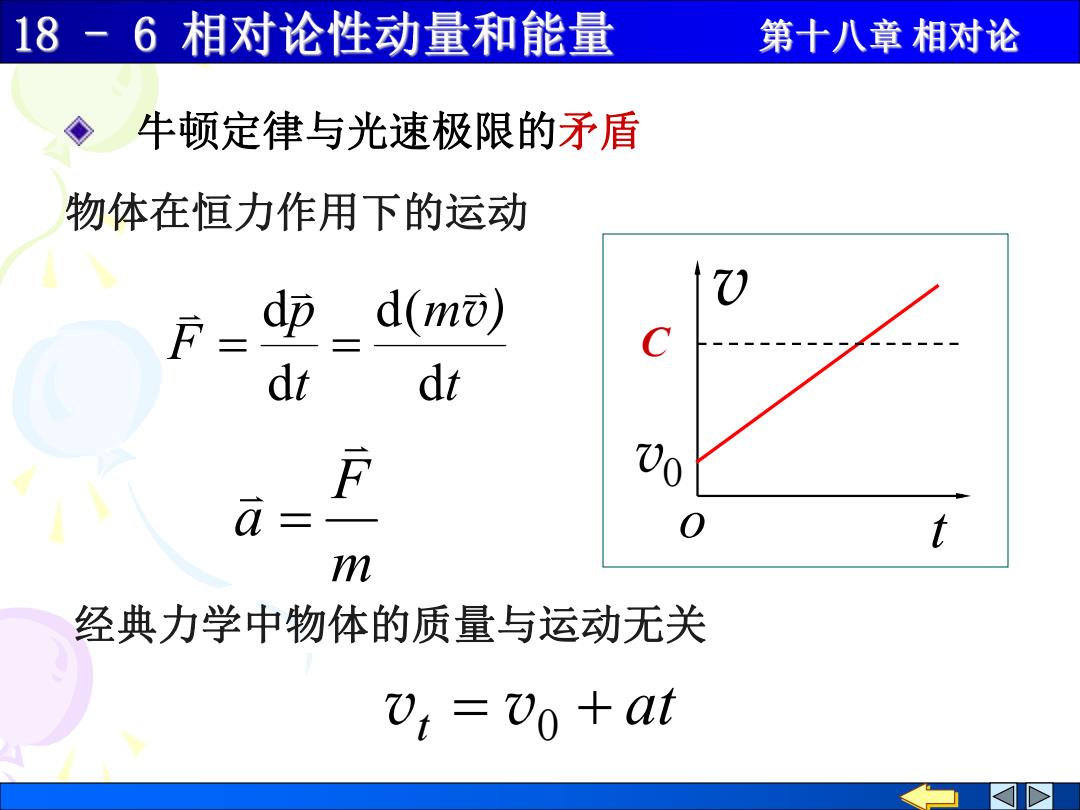
牛顿定律与光速极限的矛盾 t m t p F d d( d d v) m F a t v C 0 v o 物体在恒力作用下的运动 at vt v0 经典力学中物体的质量与运动无关
18 -6相对论性动量和能量 第十八章相对论 动量与速度的关系 mo 1)相对论动量p= V1-B2 =0i=m元 当)<<C时 p=mō→mo m 1 2)相对论质量 mo m= V1-B2 1 mo m(o)在不同惯性系中大小不同. 静质量mo:物体相对于惯性系静止时的质量. 当)<<C时m→mo
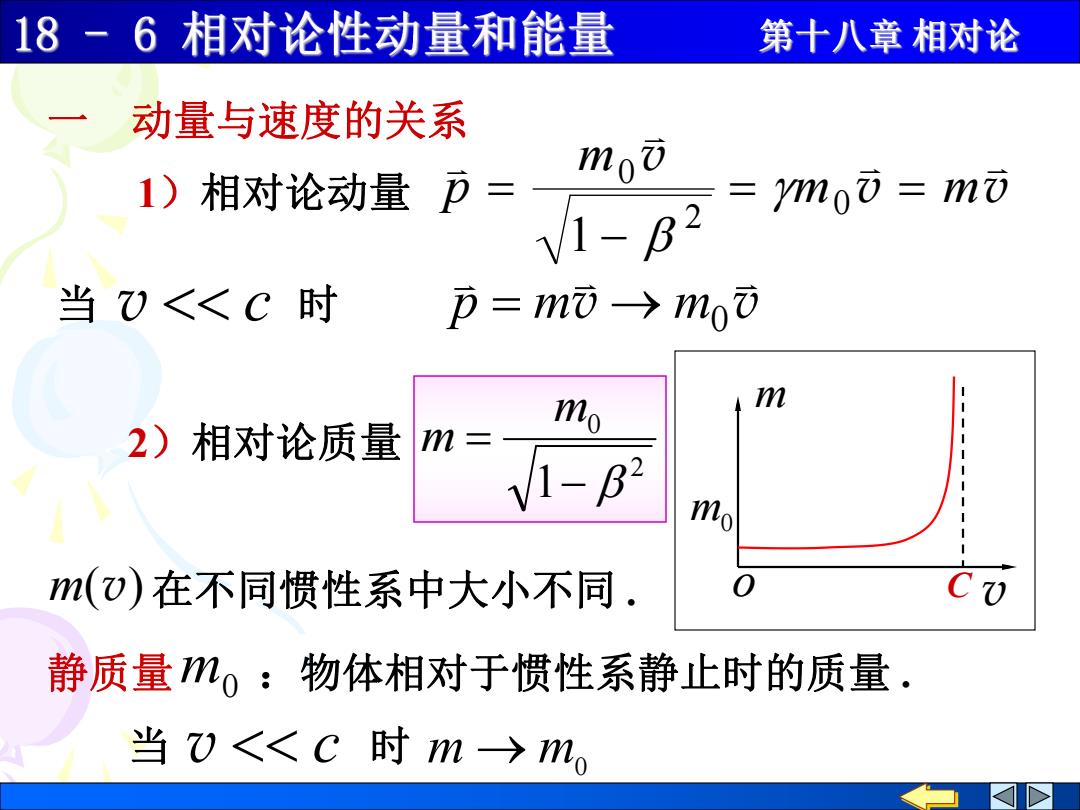
1)相对论动量 v v v m m m p 0 2 0 1 当 v c 时 v v m m0 p 一 动量与速度的关系 2)相对论质量 2 0 1 m m 静质量m0 :物体相对于惯性系静止时的质量 . m(v) 在不同惯性系中大小不同 . 当 v c 时 m m0 v m C m0 o

18-6相对论性动量和能量 第十八章相对论 狭义相对论力学的基本方程 òdx mo dō dm V1-B21 =m dt dr dt ò 当 )c时,dm/dt急剧增加,而a>0 所以光速C为物体的极限速度, 相对论动量守恒定律 当 ∑F=0时,∑p,=∑ mi0⑦i 不变. i 1-B2
二 狭义相对论力学的基本方程 ) 1 ( d d d d 2 0 v m t t p F 相对论动量守恒定律 t m t m d d d d v v 当 时, 急剧增加 , 而 , 所以光速 C 为物体的极限速度. v c dm dt a 0 i i i i i i i m F p 2 0 1 0 v 当 时, 不变 . t c m m F m d d 0 v v 当 时

18-6相对论性动量和能量 第十八章相对论 三 质量与能量的关系 动能定理△Ek-∫F.dr-mv2- 2 设 Eko=0F=Fi 0=0 dx dudg mv 利用 d(pw)=pdo+wdp和p= V1-B2 得 Ek= m v -do m,)1 积分后,得=十mc1-2-mc
三 质量与能量的关系 动能定理 2 0 2 k 2 1 2 1 E F dr mv mv x x p x p t p E F x k 0 0 0 d d d d d v 设 0 0 Ek 0 F Fi v0 2 0 2 0 2 0 k 1 1 m c m c m E 2 2 2 2 v c v c v 积分后,得 2 0 1 v m 利用 d( pv) pdv vdp 和 p v 2 v v v v 0 2 2 0 2 0 k d 1 1 c m m E 得

18-6相对论性动量和能量 第十八章相对论 =ym0 E=2+m,c2V1-2/c2-m,c2 相对论动能 Bx=me2-mc2=mc?( 当 0惯性(inertia) 物体的懒惰性就 活泼性→1 能量(energy 是物体活泼性的度量
1) 1 1 ( 2 2 0 2 0 2 k 相对论动能 E mc m c m c 2 k 0 2 1 当 v c 时, E m v m m 0 2 0 2 0 2 k E m m c 1 m c 2 2 v v c k 2 0 2 相对论质能关系 E mc m c E 爱因斯坦认为(1905) 懒惰性 惯性 ( inertia ) 活泼性 能量 ( energy ) 物体的懒惰性就 是物体活泼性的度量 . 质能关系预言:物质的质量就是能量的一种储藏

18 一6相对论性动量和能量 第十八章相对论 相对论质能关系 E=mc2=moc2+E 静能moC2: 物体静止时所具有的能量. 电子的静质量 m=0.911×10-30kg 电子的静能 m,c2=8.19×10-14J=0.511MeV 质子的静质量 m=1.673×1027kg 质子的静能 mc2=1.503×10-10J=938MeV 1千克的物体所包含的静能=9×1016J 1千克汽油的燃烧值为4.6×10焦耳
电子的静质量 0.911 10 kg 30 0 m 8.19 10 J 0.511MeV 2 14 0 电子的静能 m c 1.503 10 J 938MeV 2 10 0 质子的静能 m c k 2 0 2 相对论质能关系 E mc m c E 1千克的物体所包含的静能 9 10 J 16 1千克汽油的燃烧值为 焦耳 . 7 4.610 静能 :物体静止时所具有的能量 . 2 0 m c 质子的静质量 1.673 10 kg 27 0 m

18-6相对论性动量和能量 第十八章相对论 5)相对论能量和质量守恒是一个统一的物理规律。 质能关系预言:物质的质量就是能量的一种储藏。 例:m=1kg,E0=mc2=9×1016J 现有100座楼,每楼200套房,每套房用电功率 10000W,总功率2×108W,每天用电10小时, 年耗电量2.72×1015J,可用约33年。 电子的静质量:m=0.911×10-30kg 电子的静能:mc2=8.19×1014J=0.511MeV 质子的静质量: 质子的静能:mc2=1.503×10-10J=938MeV
例: 1kg, 9 10 J 2 16 m0 E0 m0c 现有 100 座楼,每楼 200 套房,每套房用电功率 10000 W ,总功率 ,每天用电 10 小时 , 年耗电量 ,可用约 33 年。 210 8W 2.72 10 J 15 质能关系预言:物质的质量就是能量的一种储藏。 5)相对论能量和质量守恒是一个统一的物理规律。 电子的静质量 : 0.911 10 kg 30 0 m 8.19 10 J 0.511MeV 2 14 0 电子的静能 :m c 质子的静质量 : 1.503 10 J 938MeV 2 10 0 质子的静能 : m c

18-6相对论性动量和能量 第十八章相对论 例:在一种热核反应中,各种粒子的静质量如下: H+3H>He +on 求:反应释放的能量。 氘核 (H) mp=3.3437×10-27kg 氚核 (H) m7=5.0449×10-27kg 氦核(He) me=6.6425×10-27kg 中子(n) mn=1.6750×10-27kg 反应质量亏损 △m=(no+m)-(me+mn) =0.0311×10-27(kg) 释放能量△E=△mc2=2.799×10-12J △E 1kg核燃料释放能量 =3.35×1014(J/kg) mp mr
例:在一种热核反应中,各种粒子的静质量如下: 2 1 H 3 1H 4 2 He 0 1 n 求:反应释放的能量。 ( H) 3.3437 10 kg 27 D 2 1 m ( H) 5.0449 10 kg 27 T 3 1 m ( He) 6.6425 10 kg 27 He 4 2 m ( n) 1.6750 10 kg 27 n 1 0 m 氘核 氚核 氦核 中子 0.0311 10 (kg) 27 Δ ( ) ( ) m0 mD mT mHe mn 反应质量亏损 2.799 10 J 2 12 释放能量 E mc 1 kg 核燃料释放能量 3.35 10 (J/kg) Δ 14 D T m m E

18-6相对论性动量和能量 第十八章相对论 > 锂原子的核反应 E=mc2 moc2+Eg 3Li+iH-→8Be→He+He H He 两0粒子所具有的总动能 AEk =17.3MeV 三0一 Lio 两0粒子质量比静质量增加 He △m= AE=3.08×1029kg=0.01855u c2 实验测量 mH=1.00783u mi=7.01601u mHe=4.00260u △m=0.01864u 理论计算和实验结果相符. 1u=1.66×10-27kg
Ø 锂原子的核反应 Li H Be He He 4 2 4 2 8 4 1 1 7 3 两α 粒子所具有的总动能 Ek 17.3MeV 3.08 10 kg 0.01855u 29 2 k c E m 两α 粒子质量比静质量增加 m 0.01864u mH 1.00783u 7.01601u mLi H 4.00260u m e 理论计算和实验结果相符. 实验测量 H 1 1 Li 3 7 He 4 2 He 4 2 1u 1.66 10 kg 27 k 2 0 2 E mc m c E

18-6相对论性动量和能量 第十八章相对论 0 物理意义 E=mc2 △E=(△m)c2 惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论. 相对论的质能关系为开创原子能时代提供了理 论基础,这是一个具有划时代的意义的理论公式
物理意义 2 E mc 2 E (m)c 惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论 . 相对论的质能关系为开创原子能时代提供了理 论基础 , 这是一个具有划时代的意义的理论公式