14-2简谐运动中的振幅周期频率和相位 第十四章机械振动 振幅 x一t图 A=Xmax 二周期、频率 x=Acos(ot+o) Acos o(t+T)+o] 2元 弹簧振子周期 周期 T= 0 m T=2π 1 k 频率 V= T 2元 2元 周期和频率仅与振动系 圆频率0=2πV= 统本身的物理性质有关
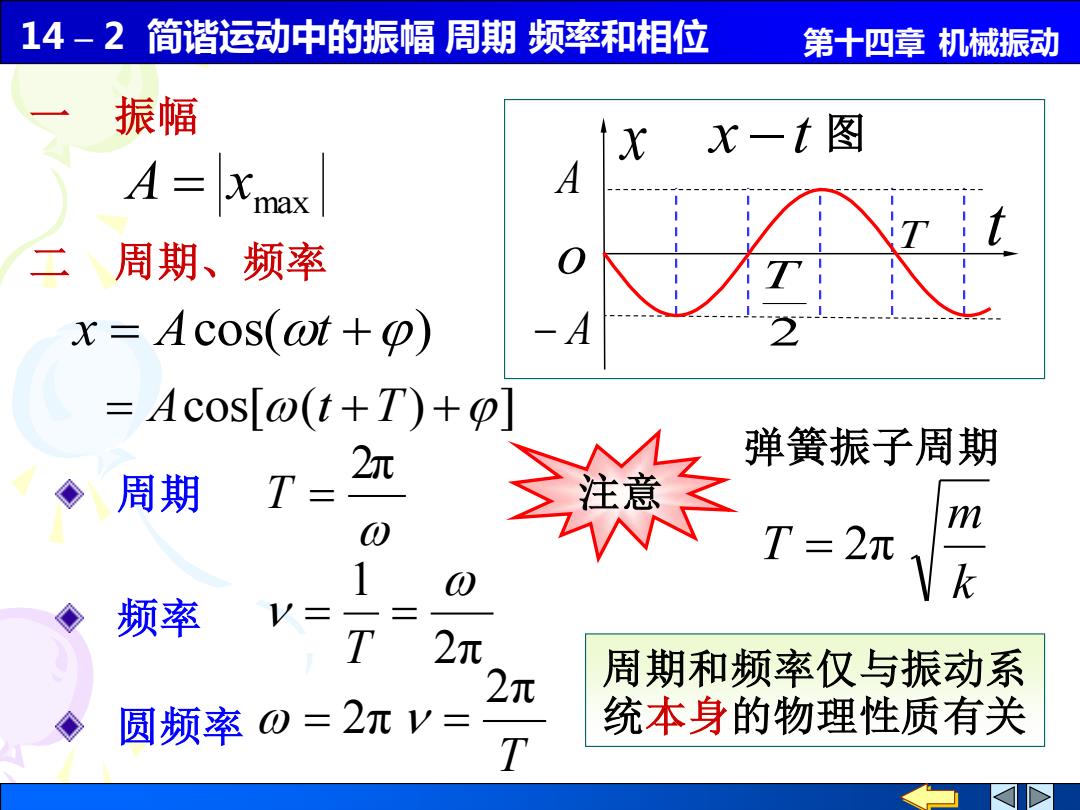
14 – 2 简谐运动中的振幅 周期 频率和相位 第十四章 机械振动 x = Acos(t +) 一 振幅 max A = x 二 周期、频率 k m T = 2π 弹簧振子周期 2π 周期 T = 2π 1 = = T 频率 T 2π 圆频率 = 2π = = Acos[(t +T) +] 周期和频率仅与振动系 统本身的物理性质有关 注意 x −t 图 A − A x T 2 T t o

14-2简谐运动中的振幅周期频率和相位 第十四章机械振动 简谐运动中,X和) x-t图 间不存在一一对应的关系 A ∫x=Acos(ot+p) Lv=-Awsin(wt+o) 三 相位 at+o 1)0t+⑩>(x,))存在一一对应的关系: 2)相位在0~2元内变化,质点无相同的运动状态; 相差2n元(为整数)质点运动状态全同.(周期性) 3) 初相位0(t=O)描述质点初始时刻的运动状态. (p取[-兀→元]或[0>2π])
14 – 2 简谐运动中的振幅 周期 频率和相位 第十四章 机械振动 1) t + → (x,v) 存在一一对应的关系; 2)相位在 0 ~ 2π 内变化,质点无相同的运动状态; 三 相位 t + 3)初相位 (t = 0) 描述质点初始时刻的运动状态. 相差 2nπ (n 为整数 ) 质点运动状态全同.(周期性) ( 取 [−π →π] 或 [0→2π] ) x −t 图 A − A x T 2 T t o v = −A sin(t +) x = Acos(t +) 简谐运动中, 和 间不存在一一对应的关系. x v v v v

14-2简谐运动中的振幅周期频率和相位 第十四章机械振动 四常数A和卫的确定 x=Acos(ot+o) Lv=-A@sin(at+o) 初始条件t=0x=x0)=V0 2 2 → 00 tanΦ 00 wxo 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定
14 – 2 简谐运动中的振幅 周期 频率和相位 第十四章 机械振动 2 2 2 0 0 v A = x + 0 0 tan x − v = 四 常数 A 和 的确定 = 0 = 0 v = v0 初始条件 t x x x0 = Acos v0 = −Asin 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. v = −A sin(t +) x = Acos(t +)
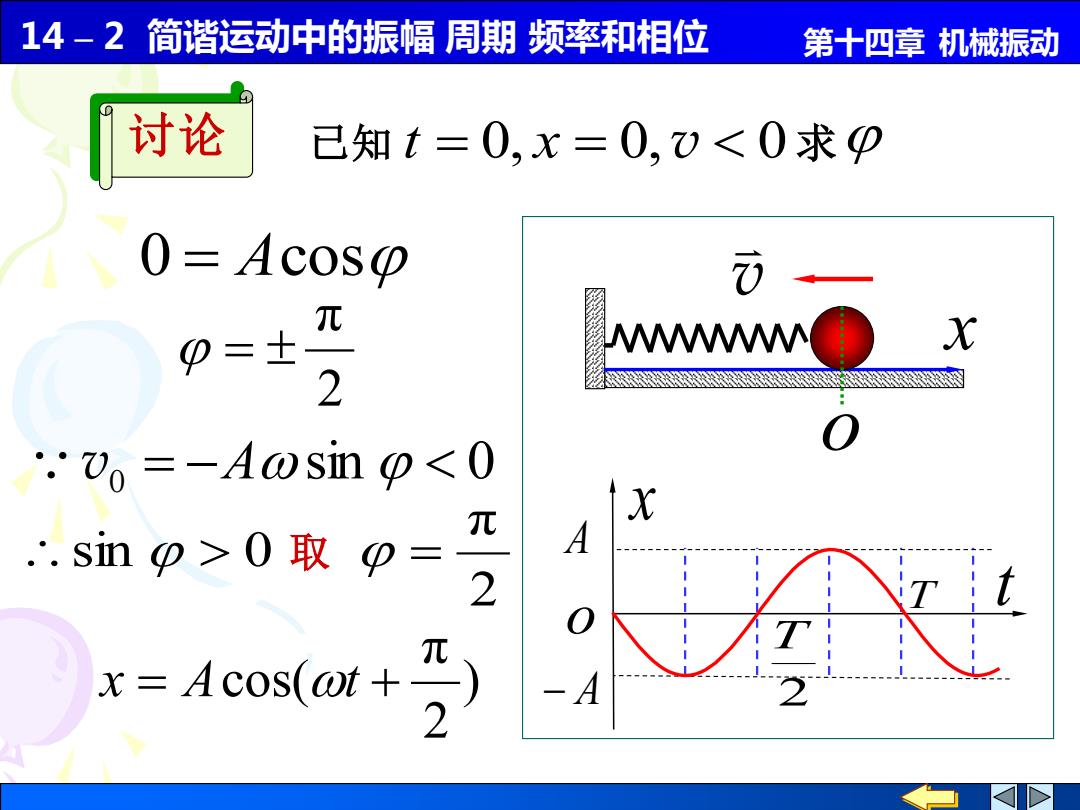
14-2简谐运动中的振幅周期频率和相位 第十四章机械振动 讨论 已知t=0,x=0,)0取p= A 2 x =Acos(wt+ 2
14 – 2 简谐运动中的振幅 周期 频率和相位 第十四章 机械振动 0 = Acos 2 π = v0 = −Asin 0 2 π sin 0 取 = 讨论 已知 t = 0, x = 0, v 0 求 x v o ) 2 π x = Acos(t + A − A x T 2 T t o