
历安毛子枚大学 图神经网络(下) XIDIAN UNIVERSITY 1.GraphSAGE 2.深度整合网络: Deep Aggregate Network(DAN)
1.GraphSAGE 2. 深度整合网络: Deep Aggregate Network(DAN) 图神经网络(下) 2

历些毛子代拔大学 (1) GraphSAGE XIDIAN UNIVERSITY GraphSAGE:一个经典的基于空间的图神经网络 ● GraphSAGE是用于节点分类任务的图神经网络 ●SAGE来源于(SAmple and aggreGatE),即对图的抽样与整合。主要包括两 个步骤:节点嵌入表示矢量的产生和参数的训练。 William L.Hamilton,Rex Ying,Jure Leskovec,"Inductive Representation Learning on Large Graphs",NIPS 2017 3
(1) GraphSAGE 3 GraphSAGE:一个经典的基于空间的图神经网络 GraphSAGE 是用于节点分类任务的图神经网络 SAGE 来源于(SAmple and aggreGatE), 即对图的抽样与整合。主要包括两 个步骤:节点嵌入表示矢量的产生和参数的训练。 William L. Hamilton, Rex Ying, Jure Leskovec, “Inductive Representation Learning on Large Graphs”, NIPS 2017

历安毛子代枚大学 (1)GraphSAGE XIDIAN UNIVERSITY GraphSAGE:一个经典的基于空间的图神经网络 1节点嵌入表达矢量的产生 Algorithm 1:GraphSAGE embedding generation(i.e.,forward propagation)algorithm Input Graph gV,)input features};depth K;weight matrices Wk {1,..);non-linearity o;differentiable aggregator functions AGGREGATE,.∀k∈{1,,K;neighborhood functionN:v→2y Output:Vector representations z for all v EV 1hg←xu,∈V; 2 for k 1...K do 3 forv∈Vdo 4 h统O←AGGREGATE(({h-1,L∈N(}): 5 蓝←o(W.CONCAT(h-1,ho 6 end 7 h的←h/川hl2,u∈y 8 end 9u←h5,u∈V
(1) GraphSAGE 4 GraphSAGE:一个经典的基于空间的图神经网络 1 节点嵌入表达矢量的产生

历安毛子代枚大等 (1)GraphSAGE XIDIAN UNIVERSITY 如图所示,模型中有K个整合函数,分别记为AGGREGATE,还有K个权矩阵 W,k∈{1,.,K。整合函数用于从邻居节点整合信息,与自身信息拼接,通 过加权矩阵得到当前自身的表示。在这个阶段,总是认为模型的参数是固定的 (已经训练好的),具体来说,就是模型的K个整合函数的参数是已知的。 Algorithm 1:GraphSAGE embedding generation(i.e.,forward propagation)algorithm Input Graph G(V,E);input features {x,Vv V;depth K;weight matrices W,1,.);non-linearity o;differentiable aggregator functions AGGREGATEK,∀k∈{1,,K};neighborhood function:v→2y Output:Vector representations z for all vV 1hg←xm,u∈V; 2 for =1...K do 3 forv∈Vdo 4 h回←AGGREGATEk({h-1,u∈N(u}: h暗←a(W.CONCAT(h-1,ho) 6 end 7 h5←h5/川hll2,oey 8 end 5 9zw←h,uey
(1) GraphSAGE 5 如图所示,模型中有K个整合函数,分别记为AGGREGATEk,还有K个权矩阵 Wk , k∈{1,…,K}。整合函数用于从邻居节点整合信息,与自身信息拼接,通 过加权矩阵得到当前自身的表示。在这个阶段,总是认为模型的参数是固定的 (已经训练好的),具体来说,就是模型的K个整合函数的参数是已知的

历安毛子代枚大” (1)GraphSAGE XIDIAN UNIVERSITY 在图中,网络的图G={V,E}以及节点的特征x是输入。h代表在第k步节点y, 的表示。可以看出,每一次迭代,每个节点从它的邻居节点整合信息,随着 迭代次数增加(或者搜索深度的增加),图中距离一个节点更远的信息不断 整合到节点中。 第一步:邻居表达整合。每个节点v整合它的直接邻居节点的表达{h, y,∈N()},形成一个矢量hm。可以看到,第步整合的结果依赖于上一步( k-1步)的节点的表达,在k=0时的节点的表达是节点的特征x。 ·第二步:拼接。将邻居表达整合结果hm与节点的上一步表达hl进行拼接 ,形成拼接矢量CONCAT(h,hMm)。 第三步:全连接层。拼接矢量通过全连接层(参数W),以非线性激活函数 o输出,形成节点y,的当前层表达h。 第四步:当k=K时,形成最终节点的表达z=hK。 6
(1) GraphSAGE 6 • 在图中,网络的图G={V,E}以及节点的特征xi是输入。hvi k代表在第k步节点vi 的表示。可以看出,每一次迭代,每个节点从它的邻居节点整合信息,随着 迭代次数增加(或者搜索深度的增加),图中距离一个节点更远的信息不断 整合到节点中。 • 第一步:邻居表达整合。每个节点vi整合它的直接邻居节点的表达{hvj k-1 , vj∈N(vi )},形成一个矢量hN(vi) k。可以看到,第k步整合的结果依赖于上一步( k-1步)的节点的表达,在k=0时的节点的表达是节点的特征xi。 • 第二步:拼接。将邻居表达整合结果hN(vi) k与节点的上一步表达hvi k-1进行拼接 ,形成拼接矢量CONCAT(hvi k-1 , hN(vi) k )。 • 第三步:全连接层。拼接矢量通过全连接层(参数W),以非线性激活函数 σ输出,形成节点vi的当前层表达hvi k 。 • 第四步:当k=K时,形成最终节点的表达zvi=hvi K

历安毛子代枚大学 (1)GraphSAGE XIDIAN UNIVERSITY 整合函数(卷积操作)。有三种整合函数(图中的整合加拼接), (1)平均整合: CONCAT(1,hvi)=mean(hh,VvjE N(vi)), (6-1) 式(6-1)的操作可以理解为卷积,卷积的结果就是将节点x及其邻居在上一步 的表示进行平均: (2)LSTM aggregator; (3)Pooling aggregator:池化整合是一种对称可训练的整合方法,每个邻居节 点的表达矢量独立通过一个神经网络,最大池化操作以整合邻居节点信息。 Wpoot?是神经网络参数。 AGGREGATEROOL max({(WpooLh1),Vvj E N(vi)}). (6-2) 7
(1) GraphSAGE 7 • 整合函数(卷积操作)。有三种整合函数(图中的整合加拼接), (1)平均整合: CONCAT ℎ𝑣𝑖 𝑘−1 , ℎ𝑁(𝑣𝑖) 𝑘 = 𝑚𝑒𝑎𝑛 ℎ𝑣𝑖 𝑘−1 ∪ ℎ𝑣𝑗 𝑘−1 , ∀𝑣𝑗 ∈ 𝑁(𝑣𝑖) , (6-1) 式(6-1)的操作可以理解为卷积,卷积的结果就是将节点xi及其邻居在上一步 的表示进行平均; (2)LSTM aggregator; (3)Pooling aggregator: 池化整合是一种对称可训练的整合方法,每个邻居节 点的表达矢量独立通过一个神经网络,最大池化操作以整合邻居节点信息。 𝑊𝑝𝑜𝑜𝑙是神经网络参数。 AGGREGATE𝑘 𝑝𝑜𝑜𝑙 = max {σ(𝑊𝑝𝑜𝑜𝑙ℎ𝑣𝑗 𝑘−1 ), ∀𝑣𝑗 ∈ 𝑁 𝑣𝑖 } , (6-2)

历柴毛子代枝大学 (1)GraphSAGE XIDIAN UNIVERSITY 关于邻居节点抽样。在图6-5的节点嵌入表达矢量生成的算法中,为了减少 计算复杂性,一个节点的邻居节点并不是它所有的邻居节点,而是进行均匀 随机抽样。限定邻居节点集合的大小,从实际邻居节点集中随机均匀抽样固 定大小的邻居节点构成邻居集合(),y,∈V。限定邻居集合大小以后,算 法的复杂性变为0(Π1S),从实验结果来说,K=2就能取得较好的性能, 且S1S2≤500。 8
(1) GraphSAGE 8 • 关于邻居节点抽样。在图6-5的节点嵌入表达矢量生成的算法中,为了减少 计算复杂性,一个节点的邻居节点并不是它所有的邻居节点,而是进行均匀 随机抽样。限定邻居节点集合的大小,从实际邻居节点集中随机均匀抽样固 定大小的邻居节点构成邻居集合N(vi ),vi∈V。限定邻居集合大小以后,算 法的复杂性变为O 𝑆𝑖 𝐾 𝑖=1 , 从实验结果来说,K=2就能取得较好的性能, 且S1·S2≤500

历些毛子代枝大学 (1)GraphSAGE XIDIAN UNIVERSITY 参数的学习 用随机梯度下降法,采用一个基于图的损失函数来调整权矩阵W Vk∈{1,.,K,以及整合函数中的参数。基于图的损失函数应使相连的节点 有相似的表示,远离的节点有不相似的表示。采用对数损失函数: Jg(zvi)=-log(a(zvizvj)-Q.Evn-Plog(-a(zvzun)),(6-2) ·式中,y,是一个在节点v,附近固定的随机游走长度内出现的节点,o是sigmoid 函数,P是负抽样的分布,Q是负抽样的个数。需要说明的是,这里反馈到 损失函数的节点的表示z,是通过节点及近邻的特征产生的,而不是训练得到 的节点的嵌入表示。 9
(1) GraphSAGE 9 2 参数的学习 • 用随机梯度下降法,采用一个基于图的损失函数来调整权矩阵Wk , ∀k∈{1,…,K}, 以及整合函数中的参数。基于图的损失函数应使相连的节点 有相似的表示,远离的节点有不相似的表示。采用对数损失函数: 𝐽𝑔 𝑧𝑣𝑖 = − log 𝜎 𝑧𝑣𝑖 𝑇 𝑧𝑣𝑗 − 𝑄 ∙ E𝑣𝑛~𝑃𝑛 log(−𝜎 𝑧𝑣𝑖 𝑇 𝑧𝑣𝑛 ), (6-2) • 式中,vj是一个在节点vi附近固定的随机游走长度内出现的节点,σ是sigmoid 函数,Pn是负抽样的分布,Q是负抽样的个数。需要说明的是,这里反馈到 损失函数的节点的表示zvi是通过节点及近邻的特征产生的,而不是训练得到 的节点的嵌入表示
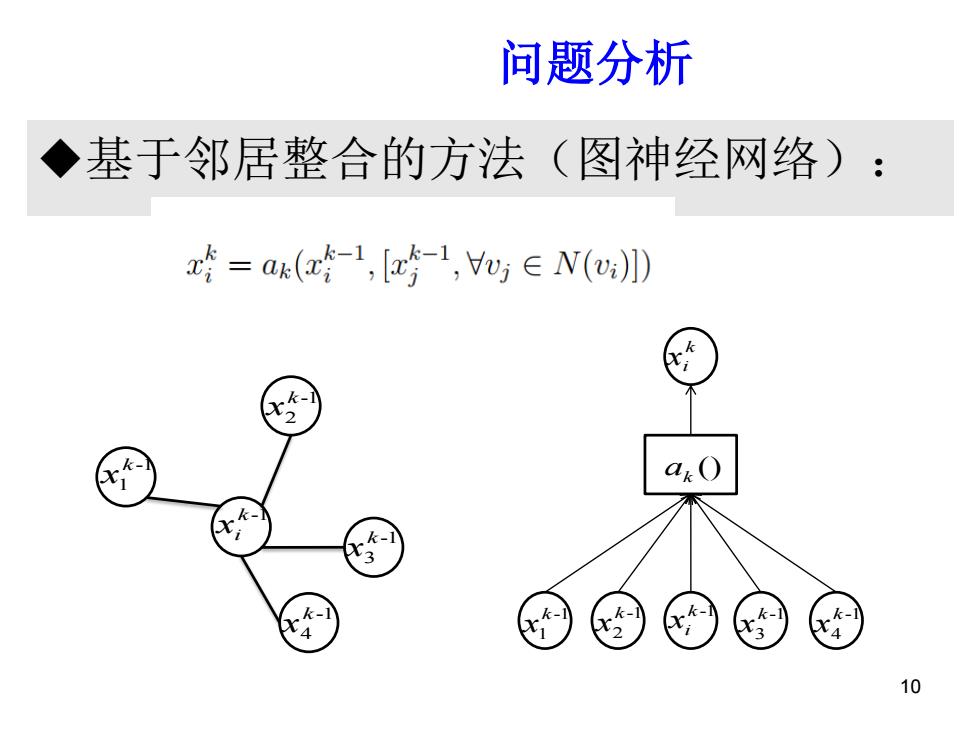
问题分析 ◆基于邻居整合的方法 (图神经网络): x=ax(a-1,[z-1,y∈V(》 k k-1 10
基于邻居整合的方法(图神经网络): 问题分析背景 10 k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x () ak k xi k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x
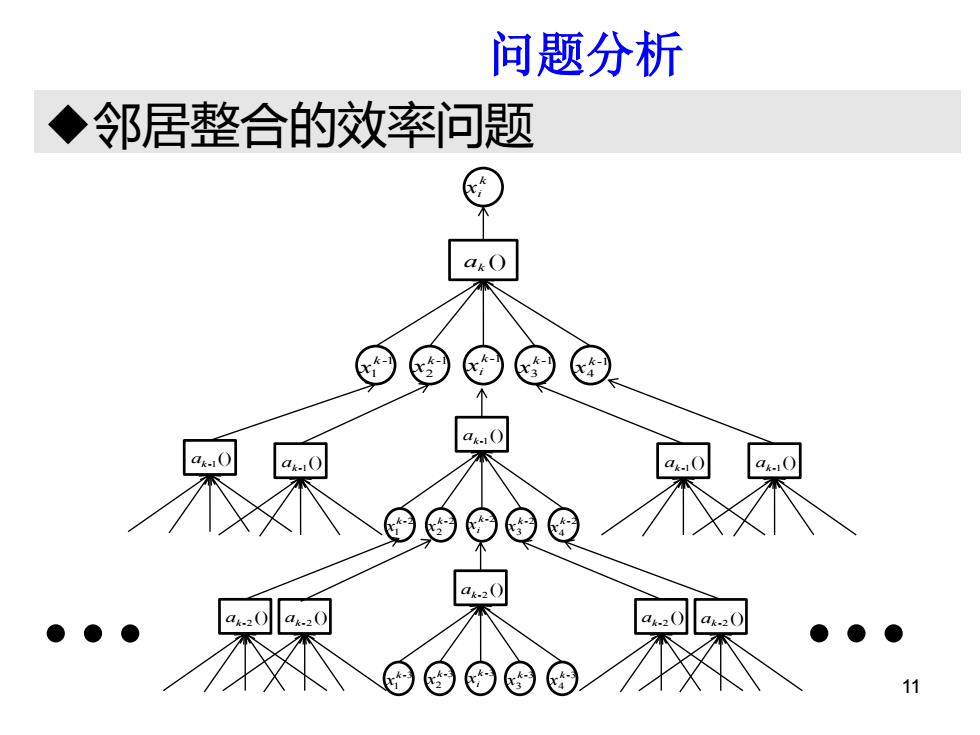
问题分析 ◆邻居整合的效率问题 a.0 a.0 11
邻居整合的效率问题 研问题分析究背景 11 () ak k xi k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x () ak-1 k -2 xi -2 1 k x -2 2 k x -2 3 k x -2 4 k x () ak-1 () ak-1 () ak-1 () ak-1 () ak-2 k -3 xi -3 1 k x -3 2 k x -3 3 k x -3 4 k x () ak-2 () ak-2 () ak-2 () ak-2