
多重均解写优化 1、占优策略与智猪博奔 2、博弈的多重纳什均衡 3、帕累托最优均衡 4、帕累托最优均衡与纳什均衡的关系 5、如何得到帕累托最优均衡
多重均衡与优化 1、占优策略与智猪博弈 2、博弈的多重纳什均衡 3、帕累托最优均衡 4、帕累托最优均衡与纳什均衡的关系 5、如何得到帕累托最优均衡

1、占优策略与智猪博弈 在博弈论(Game Theory)中,“智猪博弈”是一 个著名的例子。假设猪圈里有一头大猪、一头小 猪。猪圈的一头有猪食槽,另一头安装着控制猪 食供应的按钮,按一下按钮会有10个单位的猪食 进槽,但是谁按按钮就会首先付出2个单位的成本 若大猪先到槽边,大小猪吃到食物的收益比是 9:1;同时到槽边,收益比是7:3,小猪先到槽 边,收益比是6:4。那么,在两头猪都有智慧的 前提下,最终结果是怎样的?
1、占优策略与智猪博弈 • 在博弈论(Game Theory)中,“智猪博弈”是一 个著名的例子。假设猪圈里有一头大猪、一头小 猪。猪圈的一头有猪食槽,另一头安装着控制猪 食供应的按钮,按一下按钮会有10个单位的猪食 进槽,但是谁按按钮就会首先付出2个单位的成本 ,若大猪先到槽边,大小猪吃到食物的收益比是 9∶1;同时到槽边,收益比是7∶3;小猪先到槽 边,收益比是6∶4。那么,在两头猪都有智慧的 前提下,最终结果是怎样的?

智猪博弈 按一下按钮会有10个单位的猪食进槽, 但是谁按按钮就会首先付出2个单位的成本, 大小猪吃到食物的收益比是9:1;同时到 槽边,收益比是7:3:小猪先到槽边,收 益比是6:4。 小猪按 等待 5,1 4, 4 大猪按 等待 9,-1 0,0
智猪博弈 按一下按钮会有10个单位的猪食进槽, 但是谁按按钮就会首先付出2个单位的成本, 大小猪吃到食物的收益比是9∶1;同时到 槽边,收益比是7∶3;小猪先到槽边,收 益比是6∶4。 小猪 按 等待 大猪 按 等待 5, 1 4, 4 9, -1 0, 0

1、占优策略与智猪博弈 占优策略: 又一个例子: 两家公司,A和B,在考虎是否通过广告促销。它们的利 润额将依赖于那一家公司做广告,或者两家公司都做 广告,或者两家公司都不做广告。这些可能性和相应 的利润额被总结在旁边的矩阵里。 厂商B 做广告 不做广告 做广告 5,5 15,0 厂商A 不做广告 0,15 10,10 厂商A和厂商B的广告博弈
占优策略: 又一个例子: 两家公司, A和B,在考虑是否通过广告促销。它们的利 润额将依赖于哪一家公司做广告, 或者两家公司都做 广告, 或者两家公司都不做广告。这些可能性和相应 的利润额被总结在旁边的矩阵里。 1、占优策略与智猪博弈

1、占优策略与智猪博弈 对A, 无论B怎么做,做广告都是最优的。所以做 广告是A的占优策略。 ·对B:无论A怎么做,做广告也都是最优的。所以 做广告也是B的占优策略。 ·结论:两家厂商都应该做广告
1、占优策略与智猪博弈 • 对A, 无论B怎么做,做广告都是最优的。所以做 广告是A的占优策略。 • 对B:无论A怎么做,做广告也都是最优的。 所以 做广告也是B的占优策略。 • 结论: 两家厂商都应该做广告

1、占优策略与智猪博弈 ·定义:在参与人各自的策略集中,如果存在一个 与其他竞争对手可能采取的策略无关的最优选择, 则称其为占优策略(Dominant Strategy),与之相 对的其他策略则为劣势策略。占优策略是博弈论 (game theory)中的专业术语,所谓的占优策略 就是指无论博弈对手如何行动都属于本人最佳选 择的策略
1、占优策略与智猪博弈 • 定义:在参与人各自的策略集中,如果存在一个 与其他竞争对手可能采取的策略无关的最优选择, 则称其为占优策略(Dominant Strategy),与之相 对的其他策略则为劣势策略。占优策略是博弈论 (game theory)中的专业术语, 所谓的占优策略 就是指无论博弈对手如何行动都属于本人最佳选 择的策略

1、占优策略与智猪博奔 智猪博弈的其它例子: 。“搭便车”现象 ·穷人和富人修路博弈 ·大股东对管理者的监督 。俗语“天塌下来有大个子项着
1、占优策略与智猪博弈 智猪博弈的其它例子: • “搭便车”现象 • 穷人和富人修路博弈 • 大股东对管理者的监督 • 俗语“天塌下来有大个子顶着

占优策略和纳什均衡的比较 1. 占优策略:“不管你怎么做,我所做的 都是我能做得最好的。 2.纳什均衡: 一“给定你的做法后,我所做的是我能做得 最好的。 如果你有占优策略,你可以使用此策略,以 不变应万变; 如果你没有占优策略,你必须随机应变。在 达到了纳什均衡之后,所有参与者都没有动 机想再变了
占优策略和纳什均衡的比较 1. 占优策略:“不管你怎么做,我所做的 都是我能做得最好的。” 2. 纳什均衡: – “给定你的做法后,我所做的是我能做得 最好的。” – 如果你有占优策略, 你可以使用此策略, 以 不变应万变; – 如果你没有占优策略, 你必须随机应变。在 达到了纳什均衡之后, 所有参与者都没有动 机想再变了
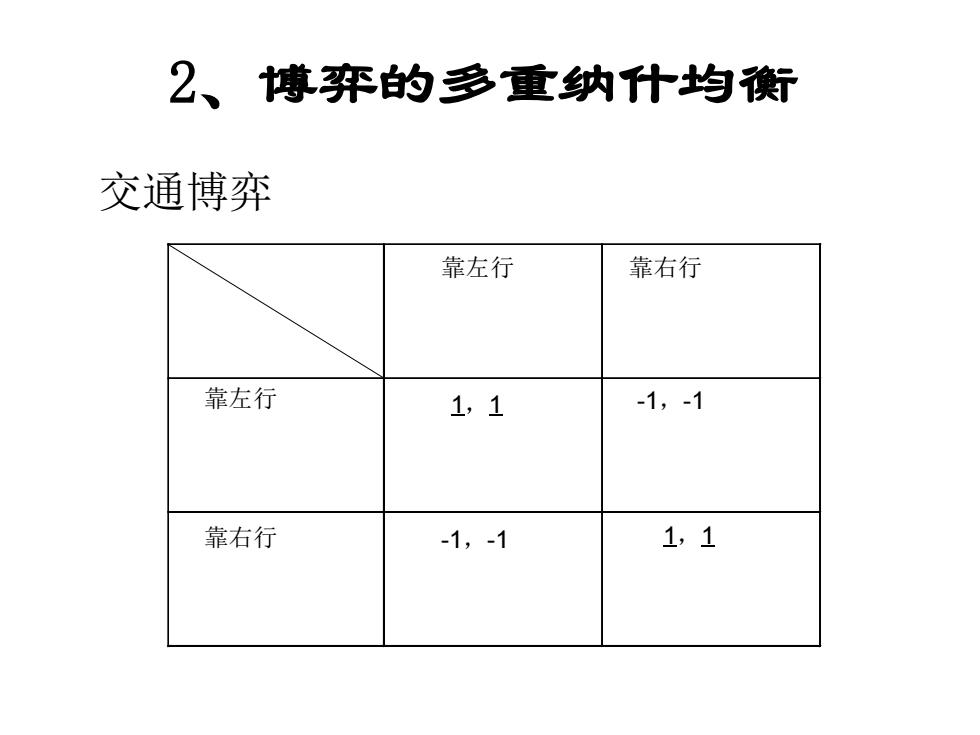
2、1 博弈的多重纳什均衡衔 交通博弈 靠左行 靠右行 靠左行 1,1 -1,-1 靠右行 -1,-1 1,1
2、博弈的多重纳什均衡 靠左行 靠右行 靠左行 靠右行 1,1 1,1 -1,-1 -1,-1 交通博弈

2、博弈的多重纳什均衡 约会博弈 芭蕾舞 足球场 芭蕾舞 1,2 0,0 足球场 0,0 2,1
约会博弈 芭蕾舞 足球场 芭蕾舞 足球场 1,2 0,0 0,0 2,1 2、博弈的多重纳什均衡