
第二节 控制系统的复数域数学模型 一、传递函数的概念 二、传递函数的性质 三、典型环节及其传递函数
一、传递函数的概念 二、传递函数的性质 三、典型环节及其传递函数 第二节 控制系统的复数域数学模型

引言 ·控制系统的微分方程:是在时域描述系统动态性能的数 学模型,在给定外作用及初始条件下,求解微分方程可以 得到系统的输出响应。但如果系统的某个参数变化或者结 构形式改变时,便需要重新列写并求解微分方程。 ·传递函数:对线性常微分方程进行拉氏变换,得到的系统 在复数域的数学模型--传递函数。 传递函数不仅可以表征系统的动态特性,而且可以研 究系统的结构或参数变化时对系统性能的影响。传递函数 是经典控制理论中最基本、最重要的概念
引言 • 控制系统的微分方程:是在时域描述系统动态性能的数 学模型,在给定外作用及初始条件下,求解微分方程可以 得到系统的输出响应。但如果系统的某个参数变化或者结 构形式改变时,便需要重新列写并求解微分方程。 • 传递函数:对线性常微分方程进行拉氏变换,得到的系统 在复数域的数学模型----传递函数。 传递函数不仅可以表征系统的动态特性,而且可以研 究系统的结构或参数变化时对系统性能的影响。传递函数 是经典控制理论中最基本、最重要的概念
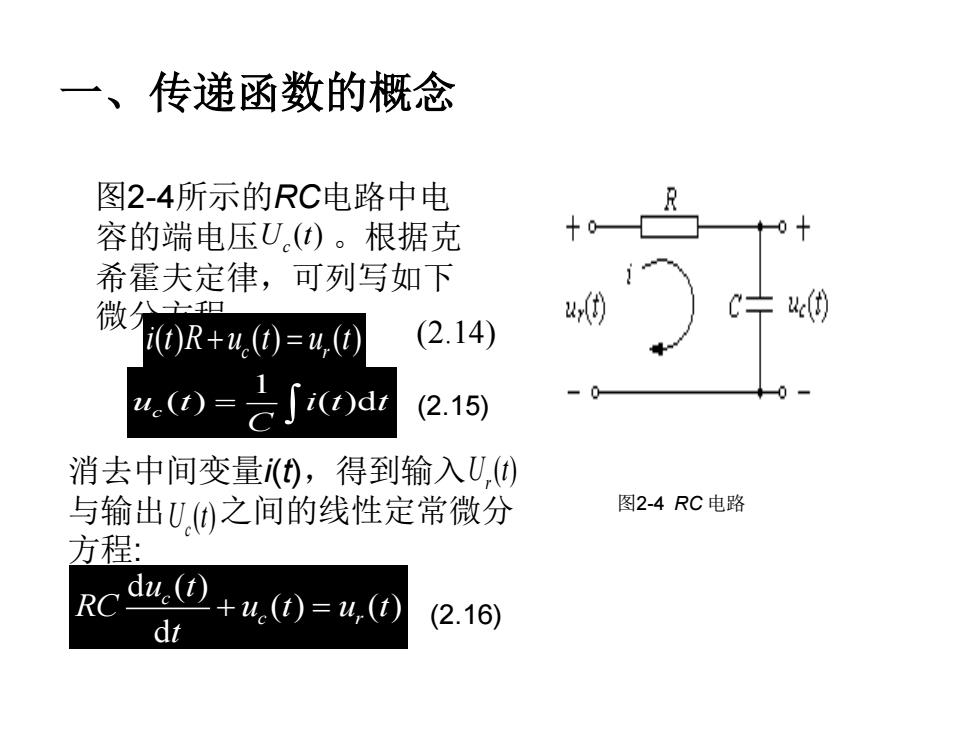
一、传递函数的概念 图2-4所示的RC电路中电 容的端电压U()。根据克 希霍夫定律,可列写如下 C卡4 1(0)R+4.()=4,() (2.14) 4.(0=∫)d (2.15) 消去中间变量(),得到输入U,) 与输出U,0之间的线性定常微分 图2-4RC电路 方程: RC du (t) 2+ue(t)=u,(t) dt (2.16)
消去中间变量i(t),得到输入 与输出 之间的线性定常微分 方程: 一、传递函数的概念 图2-4所示的RC电路中电 容的端电压 。根据克 希霍夫定律,可列写如下 微分方程: ( ) ( ) ( ) c r i t R u t u t + = (2.14) 1 u t i t t c ( ) ( )d C = (2.15) d ( ) ( ) ( ) d c c r u t RC u t u t t + = (2.16) 图2-4 RC 电路 ( ) U t c ( ) U t c ( ) U t r

现在对上述微分方程两端进行拉氏变换,并考虑电容上的 初始电压U.0),得: RCsU(s)-RCu(0)+U(s)=U,(s) (2.17) 式中U(s)一 输出电U()的拉氏变换; Us)- 输入电压U)的拉氏变换。 由上式求出Uc(S)的表达式: U.(s)= U,(S) RC RCs+1 RC+%.(O) (2.18) 当输入为阶跃电压u,()=41()时,对U(s)求拉氏反变换,即得 4.()的变化规律:
现在对上述微分方程两端进行拉氏变换,并考虑电容上的 初始电压 ,得: ( ) ( ) ( ) ( ) (2.17) RCsU s RCu U s U s c c c r − + = 0 式中 Uc(s)—— 输出电Uc(t)的拉氏变换; Ur(s)—— 输入电压Ur(t)的拉氏变换。 1 ( ) ( ) ( ) 1 1 c r c RC U s U s u RCs RCs = + + + 0 当输入为阶跃电压ur (t)= u0·1(t)时,对Uc (s)求拉氏反变换,即得 uc (t)的变化规律: 由上式求出Uc(s)的表达式: (2.18) (0) Uc
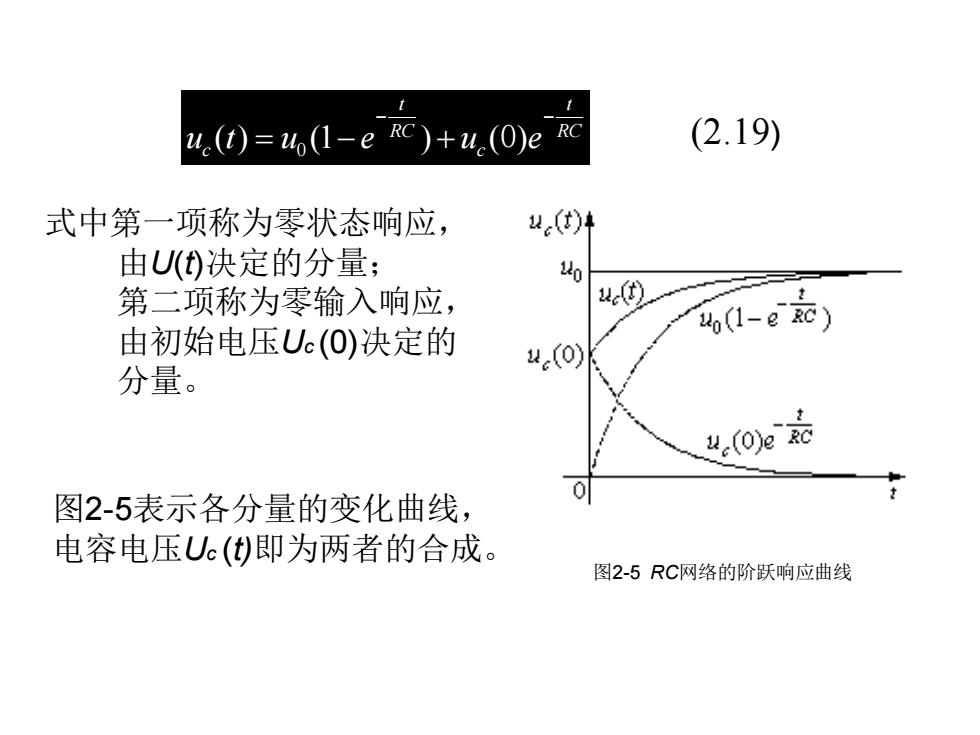
4.(t)=41-eRc)+u.(O)ec (2.19) 式中第一项称为零状态响应, -()H 由U()决定的分量; 40 第二项称为零输入响应, ue(t) uo(1-e zc) 由初始电压Uc(O)决定的 ue(0) 分量。 u(O)e Rc 图2-5表示各分量的变化曲线, 电容电压Uc(t)即为两者的合成。 图2-5RC网络的阶跃响应曲线
0 ( ) (1 ) ( ) t t RC RC u t u e u e c c − − = − + 0 (2.19) 式中第一项称为零状态响应, 由U(t)决定的分量; 第二项称为零输入响应, 由初始电压Uc (0)决定的 分量。 图2-5表示各分量的变化曲线, 电容电压Uc (t)即为两者的合成。 图2-5 RC网络的阶跃响应曲线
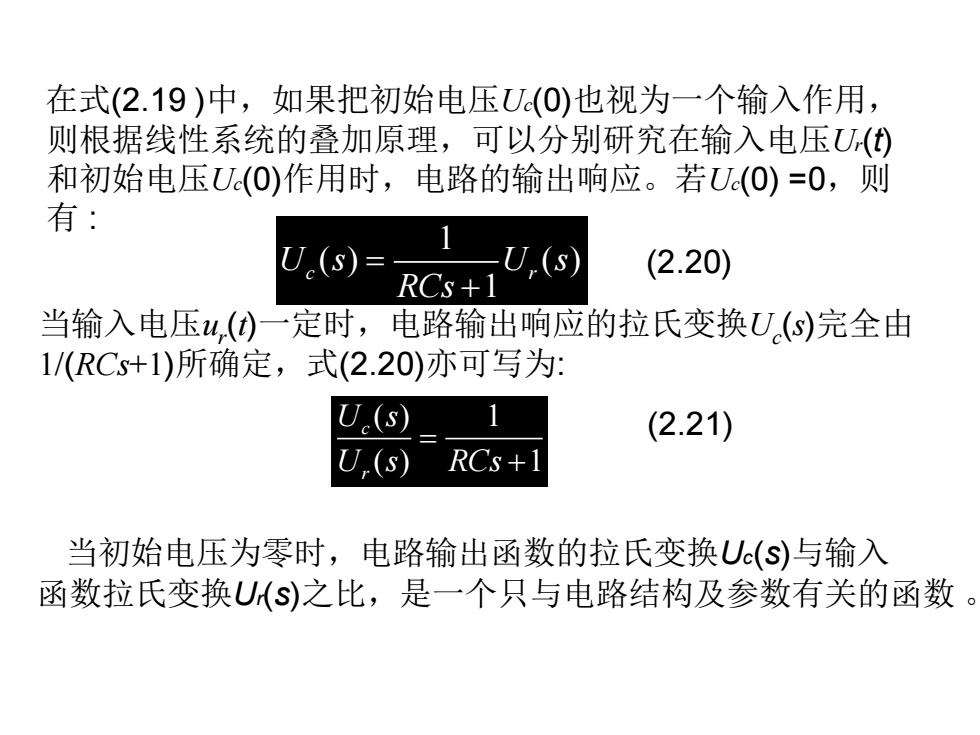
在式(2.19)中,如果把初始电压U(0)也视为一个输入作用, 则根据线性系统的叠加原理,可以分别研究在输入电压U() 和初始电压U(O)作用时,电路的输出响应。若U(O)=0,则 有: U.(s)= U,(s) (2.20) RCs+1 当输入电压u,()一定时,电路输出响应的拉氏变换U(s)完全由 1/(RCs+1)所确定,式(2.20)亦可写为: U.(s) (2.21) U(s) RCs+1 当初始电压为零时,电路输出函数的拉氏变换U(S)与输入 函数拉氏变换U(S)之比,是一个只与电路结构及参数有关的函数
在式(2.19 )中,如果把初始电压Uc(0)也视为一个输入作用, 则根据线性系统的叠加原理,可以分别研究在输入电压Ur(t) 和初始电压Uc(0)作用时,电路的输出响应。若Uc(0) =0,则 有 : 1 ( ) ( ) 1 U s U s c r RCs = + (2.20) 当输入电压ur (t)一定时,电路输出响应的拉氏变换Uc (s)完全由 1/(RCs+1)所确定,式(2.20)亦可写为: ( ) 1 ( ) 1 c r U s U s RCs = + (2.21) 当初始电压为零时,电路输出函数的拉氏变换Uc(s)与输入 函数拉氏变换Ur(s)之比,是一个只与电路结构及参数有关的函数
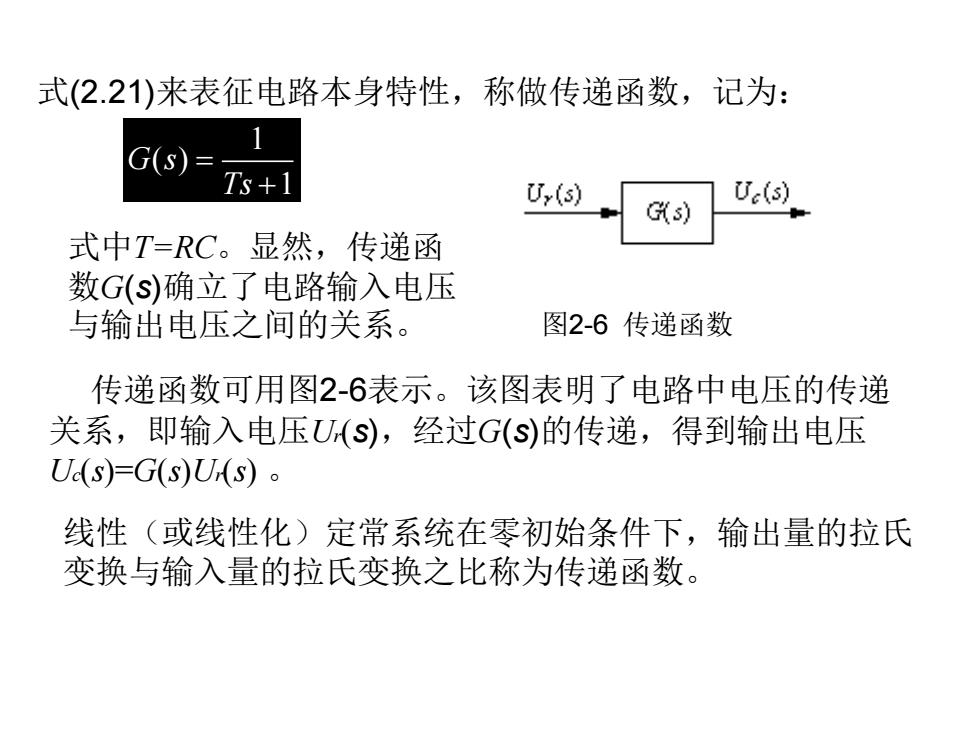
式(2.21)来表征电路本身特性,称做传递函数,记为: G(s)= Ts +i U,(s) Ue(s) Ks) 式中T=RC。显然,传递函 数G(s)确立了电路输入电压 与输出电压之间的关系。 图2-6传递函数 传递函数可用图2-6表示。该图表明了电路中电压的传递 关系,即输入电压U(S),经过G(S)的传递,得到输出电压 U(S)=G(S)U(S)。 线性(或线性化)定常系统在零初始条件下,输出量的拉氏 变换与输入量的拉氏变换之比称为传递函数
式(2.21)来表征电路本身特性,称做传递函数,记为: 1 ( ) 1 G s Ts = + 式中T=RC。显然,传递函 数G(s)确立了电路输入电压 与输出电压之间的关系。 图2-6 传递函数 传递函数可用图2-6表示。该图表明了电路中电压的传递 关系,即输入电压Ur(s),经过G(s)的传递,得到输出电压 Uc(s)=G(s)Ur(s) 。 线性(或线性化)定常系统在零初始条件下,输出量的拉氏 变换与输入量的拉氏变换之比称为传递函数

若线性定常系统由下述n阶微分方程描述: d” d- c0)+a,irc0++a -c(t)+ac(t) (2.22) d =bm d- -0+b-g0t+0+b0 式中C)是系统输田重,)是系统御人軍, (i=1,2…,n),b0j=1,2,…,m)是与系统构参数有关的常系 数。 令C(s)=L[c(],R(s)=L[()小,在初始条件为零时,对式 (2.22)进行拉氏变换,可得到s的代数方程: [ans”+an-1s”-+…+a4s+a]C(s) =[bs"+bmis"++bs+bo]R(S)
若线性定常系统由下述n阶微分方程描述: 1 1 1 0 1 1 1 1 0 1 d d d ( ) ( ) ( ) ( ) d d d d d d ( ) ( ) ( ) ( ) d d d n n n n n n m m m m m m a c t a c t a c t a c t t t t b r t b r t b r t b r t t t t − − − − − − + + + + = + + + + (2.22) 式中c(t)是系统输出量,r(t)是系统输入量,ai (i=1,2,…,n), bj(j=1,2,…,m)是与系统构参数有关的常系 数。 令C(s)=L[c(t)],R(s)=L[r(t)],在初始条件为零时,对式 (2.22)进行拉氏变换,可得到s的代数方程: 1 1 1 0 1 1 1 0 [ ] ( ) [ ] ( ) n n n n m m m m a s a s a s a C s b s b s b s b R s − − − − + + + + = + + + +

由传递函数的定义,线性定常系统的传递函数: G(s)= C(S)bns"+bmis"++bs+bo M(s (2.23) Ry)a,s”+ans++as+a D(s) 式中M(s)=bmm+bmm1+…+bs+b为传递函数的分子多项式: D(s=am”+an-1-1+…+a1+a为传递函数的分母多项式。 传递函数是在初始条件为零(或称零初始条件)时定义的。 控制系统的零初始条件有两方面的含义,一系统输入量及其各 阶导数在t=0时的值均为零;二系统输出量及其各阶导数在t=0 时的值也为零
由传递函数的定义,线性定常系统的传递函数: 1 1 1 0 1 1 1 0 ( ) ( ) ( ) ( ) ( ) m m m m n n n n C s M s b s b s b s b G s R s a s a s a s a D s − − − − + + + + = = = + + + + 式中 M(s)= bm s m+bm-1 s m-1+…+b1 s+b0为传递函数的分子多项式; D(s)= an s n+an-1 s n-1+…+a1 s+a0为传递函数的分母多项式。 (2.23) 传递函数是在初始条件为零(或称零初始条件)时定义的。 控制系统的零初始条件有两方面的含义,一系统输入量及其各 阶导数在t =0时的值均为零;二系统输出量及其各阶导数在t =0 时的值也为零

二、传递函数的性质 从线性定常系统传递函数的定义式(2.23)可知,传递函数具 有以下性质: 1.传递函数是复变量s的有理真分式函数,分子的阶数m小 于或等于分母的阶数n(m≤n),且所有系数均为实数。 2.传递函数只取决于系统和元件的结构和参数,与外作用 及初始条件无关。 3.传递函数的零、极点分布图也表征了系统的动态性能。 将式(2.23)中分子多项式及分母多项式因式分解后,写为如 下形式: G(s)= C(s) =k(+(S+2…(心+m R(s) (s+p(s+P2)…(S+pn (2.24)
二、传递函数的性质 从线性定常系统传递函数的定义式(2.23)可知,传递函数具 有以下性质: 1.传递函数是复变量s的有理真分式函数,分子的阶数m小 于或等于分母的阶数n (m≤n) ,且所有系数均为实数。 2.传递函数只取决于系统和元件的结构和参数,与外作用 及初始条件无关。 1 2 1 2 ( ) ( )( ) ( ) ( ) ( ) ( )( ) ( ) m n C s s z s z s z G s k R s s p s p s p + + + = = + + + (2.24) 3.传递函数的零、极点分布图也表征了系统的动态性能。 将式(2.23)中分子多项式及分母多 项式因式分解后,写为如 下形式: