
第二章 控制系统数学模型
控制系统数学模型 第二章

提要 1.描述系统各变量之间关系的数学表达式,叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述(例如微分方 程、传递函数等)。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容,与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述
提要 1.描述系统各变量之间关系的数学表达式,叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述(例如微分方 程、传递函数等)。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容,与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述

数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程,可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下(即变量的各阶导数 为零),描述变量之间关系的代数方程。 建立系统数学模型时,必须: ()全面了解系统特性,确定研究目的以及准确性要求,决定 能否忽略一些次要因素而简化系统的数学模型。 (2)根据所应用的系统分析方法,建立相应形式的数学模型。 建立系统的数学模型主要有两条途径: 1.分析法。 2.实验法。即根据对系统的观察,通过测量所得到的输入、输 出数据,推断出系统的数学模型
数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程,可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下(即变量的各阶导数 为零),描述变量之间关系的代数方程。 建立系统数学模型时,必须: (1) 全面了解系统特性,确定研究目的以及准确性要求,决定 能否忽略一些次要因素而简化系统的数学模型。 (2) 根据所应用的系统分析方法,建立相应形式的数学模型。 建立系统的数学模型主要有两条途径: 1.分析法。 2.实验法。即根据对系统的观察,通过测量所得到的输入、输 出数据,推断出系统的数学模型

第一节控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述,微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下: (1)适当简化,忽略一些次要因素。 (2)根据元件的物理或化学定律,列出相应的微分 方程式。 (③)消去中间变量,推出元件的输入量和输出变量 之间关系的微分方程。 (4)求出其它元件的方程。 (⑤)从所有元件的方程式中消去中间变量,最后得 到系统的输入输出微分方程
第一节 控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述,微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下: (1) 适当简化,忽略一些次要因素。 (2) 根据元件的物理或化学定律,列出相应的微分 方程式。 (3) 消去中间变量,推出元件的输入量和输出变量 之间关系的微分方程。 (4) 求出其它元件的方程。 (5) 从所有元件的方程式中消去中间变量,最后得 到系统的输入输出微分方程
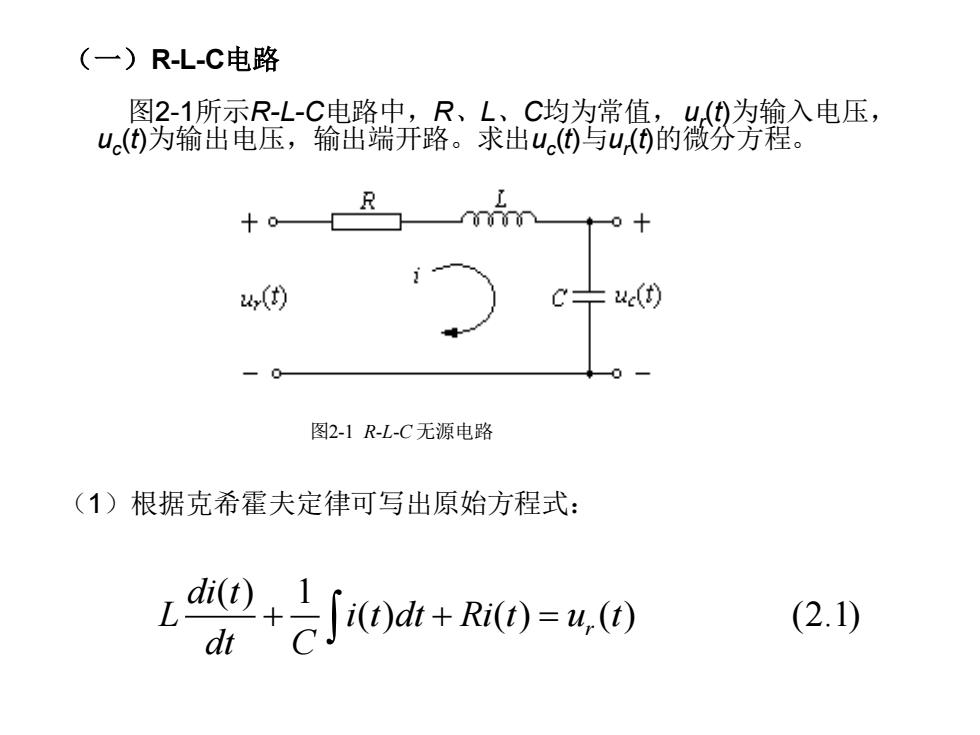
(一)RL-C电路 图2-1所示R-L-C电路中,R、L、,C均为常值,U(⑤为输入电压, u()为输出电压,输出端开路。求出u)与u①的微汾方程。 十0 () ud(t) 图2-1R-L-C无源电路 (1)根据克希霍夫定律可写出原始方程式: i+i0ot+0=e0 (2.1)
(一)R-L-C电路 图2-1所示R-L-C电路中,R、L、C均为常值,ur (t)为输入电压, uc (t)为输出电压,输出端开路。求出uc (t)与ur (t)的微分方程。 (1)根据克希霍夫定律可写出原始方程式: 图2-1 R-L-C 无源电路 ( ) 1 ( ) ( ) ( ) (2.1) r di t L i t dt Ri t u t dt C + + =

(2)式中(t)是中间变量,它与输出u.(t)有如下关系: .(=ja (2.2) (3)消去式(2.1)、式(2.2)的中间变量()后,输入输出 微分方程式: du(t) dt2 +RC du (t) 2+u.(t)=u,(t) dt (2.3) 或 d@+x du (t) dt2 dt 2+u.(0)=4,( (2.4) 式中T=LC,T,=RC为电路的时间常数,单位为秒。 式(2.3)和式(2.4)是线性定常二线性微分方程
(2)式中i(t)是中间变量,它与输出uc (t)有如下关系: (3) 消去式(2.1)、式(2.2)的中间变量i(t)后,输入输出 微分方程式: 2 2 d ( ) d ( ) ( ) ( ) d d c c c r u t u t LC RC u t u t t t + + = 或 (2.4) (2.3) 式中T1 =LC,T2 =RC为电路的时间常数,单位为秒。 式(2.3)和式(2.4)是线性定常二阶线性微分方程。 1 ( ) ( )d c u t i t t C = 1 ( ) ( )d (2.2) u t i t t c C = 2 1 2 2 d ( ) d ( ) ( ) ( ) d d c c c r u t u t T T u t u t t t + + =

二、非线性方程的线性化 几乎所有元件或系统的运动方程都是非线性的。 但对于较小的范围内的运动,把这些元件看作是线性 元件,因此可以建立线性微分方程。线性微分方程, 满足迭加原理和齐次性。 研究非线性系统在某一工作点(平衡点)附近的 性能,(如图2-2,X为平衡点,受到扰动后,()偏 离xo,产生△x(),△X)的变化过程,表征系统在X附 近的性能) 可用下述的线性化方法得到的线性模型代替非线 性模型来描述系统: 图2-2小偏差过程
二、非线性方程的线性化 几乎所有元件或系统的运动方程都是非线性的。 但对于较小的范围内的运动,把这些元件看作是线性 元件,因此可以建立线性微分方程。线性微分方程, 满足迭加原理和齐次性。 研究非线性系统在某一工作点(平衡点)附近的 性能,(如图2-2,x0为平衡点,受到扰动后,x(t)偏 离x 0,产生Δx(t),Δx(t)的变化过程,表征系统在x0附 近的性能) 可用下述的线性化方法得到的线性模型代替非线 性模型来描述系统: 图2-2 小偏差过程

设连续变化的非线性函数为y=x)。取某平衡状态A为工作 点,即=fxo)当x=x+Ax时,y=+ 设函数fx)在x,) 连续可微,则在该点附近用泰勒级数展开为: y=w)=f(x,)+( d l (x-x> 1 d'f(x) 2!dx2 21(x-x) (2.5) 当(x-x)很小时,略去高次幂相,则 y-%=f)-fx,)= (x-xo> d (2.6) 则略去增量符Ay=K△x,or,y=K,附近的线性化方程 令Ay=y-=f(x)-f(xo), △x=(x-xo), K- af(x) dx
(2.5) 当 很小时,略去高次幂相,则 (2.6) 则略去增量符号,可得到在工作点附近的线性化方程 设连续变化的非线性函数为y = f(x)。取某平衡状态A为工作 点,即 。当 时, ,设函数f(x)在 连续可微,则在该点附近用泰勒级数展开为: 0 (x x − ) 0 0 0 ( ) ( ) ( ), ( df x y y y f x f x x x x K dx 令 ), = − = − = − = 0 0 0 0 ( ) ( ) ( ) | ( x df x y y f x f x x x dx − = − = − ) 0 0 2 0 0 0 2 ( ) ( ) ( ) ( ) | ( | ( x x df x d f x y f x f x x x x x dx dx = = + − − + )+ ) 1 2 2! = = y K x or y Kx , , , 0 0 y f x = ( ) 0 x x = + x 0 y y y = + 0 0 ( , x y )

y=f) u.(1 u(t) 图2-3小偏差线性化示意图 图2-4 RL网络 例2-3,设铁芯线圈电路如图2-4所示,其磁通与线圈中电 流之间的关系如图2-5所示,试写出以为输入,为输出的 微分方程。 解(1)设铁芯线圈磁通 变化时产生的感应电势为: 图2-5磁通与线圈中电流之间的关系
2 0 0 2 d d ( ) ( ) d d f f i i , , Rn+1 0 f 0 i 图2-3 小偏差线性化示意图 图2-4 RL网络 例2-3,设铁芯线圈电路如图2-4所示,其磁通与线圈中电 流之间的关系如图2-5所示,试写出以为输入,为输出的 微分方程。 解(1)设铁芯线圈磁通 变化时产生的感应电势为: 图2-5磁通与线圈中电流之间的关系

U。=K1 do(i) (2.7) dt (2)电路微分方程为: dp(i) +Ri=K dp(i)di U.=K i +Ri dt di dt 设在平衡点的邻域内,p对的各阶导数(直至n+1) 是存在的,它可展成泰勒级数: do(i) p()=0()+( (△)2+… (2.8) 其中:△i=i-i0 当△i足够小时,略去高阶导数 p()-p(i)=( o@).△i=KA di
1 1 ( ) ( ) r d i d i di U K Ri K Ri dt di dt = + = + (2)电路微分方程为: 设在平衡点的邻域内, 对i的各阶导数(直至n+1) 是存在的,它可展成泰勒级数: 0 0 2 2 0 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) 2 ! i i d i d i i i i di di = + + + (2.7) (2.8) 1 d i( ) U K dt = 其中:Δi =i- i 0 当Δi 足够小时,略去高阶导数 0 0 ( ) ( ) ( ) ( )i d i i i i K i di − = =