
§4-2典型环节频率特性的绘制 自动控制系统通常由若干环节构成,根据它们的基本特性,可 划分成几种典型环节。典型环节的基本特性在第二章已经介 绍,本节将介绍典型环节频率特性的绘制方法。系统或环节频 率特性的绘制有多种方式,本节主要介绍应用较为广泛的极坐 标图(Nyquist)和伯德图(Bode)。 一、典型环节的幅相特性曲线(极坐标图) 以角频率ω为参变量,根据系统的幅频特性G(o)和相频特性 ∠G(jo)在复平面GH]业绘制出的频率特性叫做幅相特性曲线或频 率特性的极坐标图。它是当角频率ω从0到无穷变化时,矢量 G(o)H(Ujo)e的矢端在[G(jo)平面上描绘出的曲线。 曲线是关于实轴对称的
1 § 4-2 典型环节频率特性的绘制 G( j) G( j) G( j) j G( j )H( j ) e GH 自动控制系统通常由若干环节构成,根据它们的基本特性,可 划分成几种典型环节。典型环节的基本特性在第二章已经介 绍,本节将介绍典型环节频率特性的绘制方法。系统或环节频 率特性的绘制有多种方式,本节主要介绍应用较为广泛的极坐 标图(Nyquist)和伯德图(Bode)。 一、典型环节的幅相特性曲线(极坐标图) 以角频率ω为参变量,根据系统的幅频特性 和相频特性 在复平面 上绘制出的频率特性叫做幅相特性曲线或频 率特性的极坐标图。它是当角频率ω从0到无穷变化时,矢量 的矢端在 平面上描绘出的曲线。 曲线是关于实轴对称的

(一)放大环节(比例环节) 放大环节的传递函数为G(S)=K (4-18) 其对应的频率特性是G(jo)=K (4-19) 其幅频特性和相频特性分别为 G(jo)=K (4-20) ∠G(jo)=0° (4-21) 频率特性如图4-2所示。 由图4-2可看出放大环节 的幅频特性为常数K,相频特 K R。 性等于零度,它们都与频率无 关。理想的放大环节能够无失 0 0=0→∞ 真和无滞后地复现输入信号。 图4-2放大环节的频率响应2
2 (一) 放大环节(比例环节) G( j) = K 放大环节的传递函数为 G(s) = K 其对应的频率特性是 (4-18) (4-19) . 0 = 0→ m I K R e 图4-2 放大环节的频率响应 频率特性如图4-2所示。 G( j) = K 0 G( j) = 0 其幅频特性和相频特性分别为 (4-20) (4-21) 由图4-2可看出放大环节 的幅频特性为常数K,相频特 性等于零度,它们都与频率无 关。理想的放大环节能够无失 真和无滞后地复现输入信号

(二)积分环节 积分环节的传递函数为 1 G(S)= (4-22) S 其对应的频率特性是 G(j0)= j⊙ (4-23) 幅频特性和相频特性分别为 m [G] Ke-a (4-24) 0=O R ∠G(j0)=-arctg8=-90° (4-25) 0 900 频率特性如图4-3所示。由图可 看出,积分环节的相频特性等于 ⊙→0 -900,与角频率w无关, 图43积分环节的频率响应 3
3 (二) 积分环节 积分环节的传递函数为 (4-22) 其对应的频率特性是 (4-23) 幅频特性和相频特性分别为 (4-24) (4-25) 频率特性如图4-3所示。由图可 看出,积分环节的相频特性等于 -900 ,与角频率ω无关, s G s 1 ( ) = j G j 1 ( ) = 1 1 ( ) = = j G j 0 90 0 ( ) = − = − G j arctg 图4-3 积分环节的频率响应 R e m I = →0 G 0 −90

表明积分环节对正弦输入信号有90°的滞后作用;其幅频特性等 于1,是ω的函数,当ω由零变到无穷大时,输出幅值则由 无翳大衰减至零。在GU平面上,积分环节的频率特性与负 虚轴重合。 (三) 惯性环节 惯性环节的传递函数为 1 G(S)= Ts +1 (4-26) 其对应的频率特性是 G(j0)= iTo+1 (4-27) 幅频特性和相频特性分别是 4
4 表明积分环节对正弦输入信号有90o的滞后作用;其幅频特性等 于 ,是ω的函数, 当ω由零变到无穷大时,输出幅值则由 无穷大衰减至零。在 平面上,积分环节的频率特性与负 虚轴重合。 (三) 惯性环节 惯性环节的传递函数为 (4-26) 其对应的频率特性是 (4-27) 幅频特性和相频特性分别是 1 G( j) 1 1 ( ) + = Ts G s 1 1 ( ) + = jT G j

G(j@)= +T2o2 (4-28) ∠G(jo)=-arctgTo (4-29) 当o=0时,G(0)=1∠G(0)=0°; 当0-时k3U7=方-0707∠0U宁=4: 当0=0时,lG(jo=0 ∠G(j∞)=-90° 当ω由零至无穷大变化时,惯性环节的频率特性在[G(jo)]平 面上是正实轴下方的半个圆周,证明如下: G(j0)- To 0+11+T”o-J1+产0 (4-30) Re(jo)小= 1+7产o=o) (4-31) 5
5 (4-28) (4-29) 当 时, ; 当 时, ; 当 时, 。 当ω由零至无穷大变化时,惯性环节的频率特性在 平 面上是正实轴下方的半个圆周,证明如下: (4-30) 令 (4-31) 2 2 1 1 ( ) T G j + = G( j) = −arctgT = 0 G( j0) =1 0 G( j0) = 0 T 1 = 0.707 2 1 ) 1 ( = = T G j 0 ) 45 1 ( = − T G j = G( j) = 0 ( ) 90o = − G j G( j) 2 2 2 2 1 1 1 1 1 ( ) T T j j T T G j + − + = + = ( ) 1 1 Re ( ) 2 2 u T G j = + =

Im[G(jo)]=- To 1+To2*(@) (4-32) 则有uo)+[r (7o(%- (4-33) 这是一个标准圆方程,其圆心坐标是(30半径为号。且 当o由0→0时,∠G)0)由0°→-90%,说明惯性环节的频率特 性在[G(0)平面上是实轴下方半个圆周,如图4-4所示。惯 性环节是一个低通滤波环节和相位滞后环节。在低频范围内, 对输入信号的幅值衰减较小,滞后相移也小,在高频范围内, 幅值衰减较大,滞后相角也大,最大滞后相角为90。 6
6 (4-32) 则有 (4-33) 这是一个标准圆方程,其圆心坐标是 ,半径为 。且 当ω由 时, 由 ,说明惯性环节的频率特 性在 平面上是实轴下方半个圆周,如图4-4所示。惯 性环节是一个低通滤波环节和相位滞后环节。在低频范围内, 对输入信号的幅值衰减较小,滞后相移也小,在高频范围内, 幅值衰减较大,滞后相角也大,最大滞后相角为900 。 ( ) 1 Im ( ) 2 2 v T T G j = + = − 2 2 2 2 2 2 2 2 2 2 1 2 1 1 1 1 ( ) 2 1 ( ) = + − + − + = + − T T T u v ,0 2 1 2 1 0 → G( j) 0 0 0 → −90 G( j)
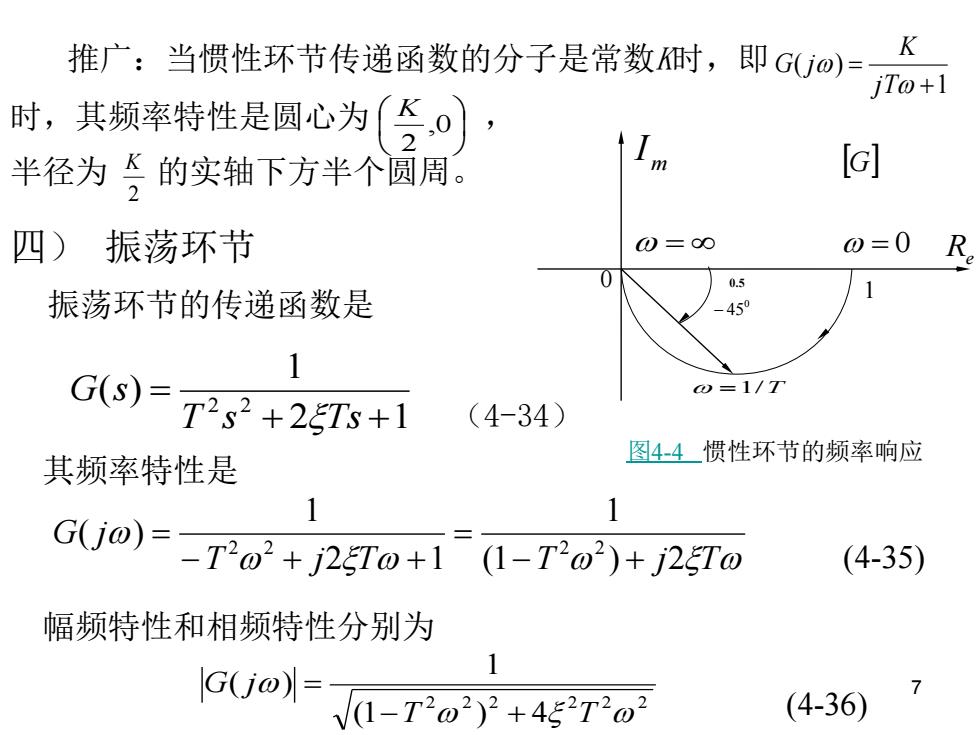
推广:当惯性环节传递函数的分子是常数时,即Gjo)= j江o+1 时,其频率特性是圆心为,0】 半径为的实轴下方半个圆周。 Ic] 四) 振荡环节 0=∞ 0=0 0.5 振荡环节的传递函数是 -450 G(s)= ⊙=1/T T2s2+25Ts+1 (4-34) 图4-4_惯性环节的频率响应 其频率特性是 1 1 G(j0)=-T2w2+j2T0+1 (1-T2o2)+j25Tw (4-35) 幅频特性和相频特性分别为 G(j0)= 1-T2o2)2+452T2o2 (4-36)
7 推广:当惯性环节传递函数的分子是常数K时,即 时,其频率特性是圆心为 , 半径为 的实轴下方半个圆周。 四) 振荡环节 振荡环节的传递函数是 (4-34) 其频率特性是 幅频特性和相频特性分别为 1 ( ) + = jT K G j ,0 2 K 2 K 2 1 1 ( ) 2 2 + + = T s Ts G s T j T T j T G j (1 ) 2 1 2 1 1 ( ) 2 2 2 2 − + = − + + = 2 2 2 2 2 2 (1 ) 4 1 ( ) T T G j − + = . 0 − 45 0 1 0.5 =1/T 图4-4 惯性环节的频率响应 m I G = 0 Re = (4-35) (4-36)

2ETo ∠G(jo)=-arclg1-T2o2 (4-37) 当0=0时,|G(jo=1,,∠Gjo)=0°: aUo以-2w 当0=0时,G(jo=0,∠G(jo)=-180°。 振荡环节的幅频特性和相频特性均与阻尼比ξ有关,不同 阻尼比的频率特性曲线如图4-5所示。同时,当阻尼比较小时, 会产生谐振,谐振峰值M,(M,>1)和谐振频率o,由幅频特性的 极值方程解出。 品aUo--rwf+4e7ol-0 (4-38) a-71-2E2=0.-2g0<5<72) (4-39) 8
8 (4-37) 当 时, , ; 当 时, , ; 当 时, , 。 振荡环节的幅频特性和相频特性均与阻尼比ξ有关,不同 阻尼比的频率特性曲线如图4-5所示。同时,当阻尼比较小时, 会产生谐振,谐振峰值 和谐振频率 由幅频特性的 极值方程解出。 (4-38) (4-39) 2 2 1 2 ( ) T T G j arctg − = − G( j) =1 2 1 G( j ) = = 0 0 G( j) = 0 T 1 = 0 G( j) = −90 = G( j) = 0 0 G( j) = −180 ( 1) Mr Mr r ( ) (1 ) 4 0 2 2 2 2 2 2 = − + = T T d d G j d d ) 2 1 1 2 1 2 (0 1 2 2 r = − =n − T

其中@,=月 称为振荡 G 环节的无阻尼自然振 R 荡频率,它是振荡环 0=0 On 节频率特性曲线与虚 Qn M 轴的交点处的频率。 On 0 将o,代入lGjo)得 到谐振峰值M,为 图4-5 振荡环节的频率响应 (4-40) 将o,代入∠G(Uo)得到谐振相移Φ为 V1-252 .=∠G(jo,)=-arctg =-90°+arcsin V1-52 (4-41)
9 其中 称为振荡 环节的无阻尼自然振 荡频率,它是振荡环 节频率特性曲线与虚 轴的交点处的频率。 将 代入 得 到谐振峰值 为 (4-40) 将 代入 得到谐振相移φr为 T n 1 = r G( j) Mr ) 2 1 (0 2 1 1 ( ) 2 − = = r r M G j r G( j) 2 0 2 1 90 arcsin 1 2 ( ) − = − + − = G j = −arctg r r (4-41) n n Mr 0 n n r = 0 m I = r 1 Re G 图4-5 振荡环节的频率响应

振荡环节的幅值特性曲线如图4-6所示。在0o,时,Mo)迅速减小,M(o)=0.707时的频率 称为截止频率0。;频率大于o。后,输出幅值衰减很快。 当阻尼比专>1时,此 时振荡环节可等效成两个 M( 不同时间常数的惯性环节 的串联,即 0.707 G(s))=(s+1江s+0 (ξ>1) 0,0。 T1,T2为一大一小两个不同的时间 常数,小时间常数对应大的负实极 图4-6振荡环节的频率响应 点,离虚轴较远,对瞬态响应的影响较小。 10
10 振荡环节的幅值特性曲线如图 4-6 所示。在 的范 围内,随着ω的增加, 缓慢增大;当 时, 达到 最大值 ;当 时, 迅速减小, 时的频率 称为截止频率 ;频率大于 后,输出幅值衰减很快。 当阻尼比 时,此 时振荡环节可等效成两个 不同时间常数的惯性环节 的串联, 即 0 r M () =r Mr M () r M () M () = 0.707 c c 1 1 M () 0.7070 r c Mr 图4-6 振荡环节的频率响应 1 ( )( ) ( 1) 1 1 1 ( ) 1 2 + + = T s T s G s T1,T2为一大一小两个不同的时间 常数,小时间常数对应大的负实极 点,离虚轴较远,对瞬态响应的影响较小