
§4-3系统开环频率特性的绘制 系统的开环频率特性在系统的分析与综合中有 很重要的意义,本节将通过一些示例介绍系统的开 环频率特性(极坐标图和伯德图)的绘制方法和步 骤。 自动控制系统通常由若干典型环节组成,根据 它们的基本特性,可以把系统分解成一些典型环节 串联的形式,再把这些典型环节的频率特性组合起 来得到整个系统的开环频率特性。因此,绘制系统 开环频率特性的基本步骤是将系统的开环传递函数 分解成若干典型环节的串联形式
1 §4-3 系统开环频率特性的绘制 系统的开环频率特性在系统的分析与综合中有 很重要的意义,本节将通过一些示例介绍系统的开 环频率特性(极坐标图和伯德图)的绘制方法和步 骤。 自动控制系统通常由若干典型环节组成,根据 它们的基本特性,可以把系统分解成一些典型环节 串联的形式,再把这些典型环节的频率特性组合起 来得到整个系统的开环频率特性。因此,绘制系统 开环频率特性的基本步骤是将系统的开环传递函数 分解成若干典型环节的串联形式

一、 绘制系统开环频率特性-极坐标图(Nyquist)的 步骤 1. 将系统开环传递函数分解成若干典型环节的串联形式: 2. 典型环节幅频特性相乘得到系统开环幅频特性; 3. 典型环节相频特性相加得到系统开环相频特性; 4. 如幅频特性有渐近线,则根据开环频率特性表达式的实部 和虚部,求出渐近线; 5.最后在G(jw)(jω)平面上绘制出系统的极坐标图。 2
2 一、绘制系统开环频率特性---极坐标图(Nyquist)的 步骤 1. 将系统开环传递函数分解成若干典型环节的串联形式; 2. 典型环节幅频特性相乘得到系统开环幅频特性; 3. 典型环节相频特性相加得到系统开环相频特性; 4. 如幅频特性有渐近线,则根据开环频率特性表达式的实部 和虚部,求出渐近线; 5. 最后在G(jω)H(jω)平面上绘制出系统的极坐标图

二、绘制系统开环频率特性--伯德图(Bode)的步骤 1.将系统的开环传递函数写成典型环节乘积的形式: 2. 如果存在交接频率,在ω轴上标出交接频率的坐标位置; 3. 由各典型环节的对数幅频特性叠加后得到系统开环对数幅 频特性的渐近线; 4. 修正误差,画出比较精确的对数幅频特性; 5. 画出各串联典型环节相频特性,将它们相加后得到系统开 环相频特性。 3
3 1. 将系统的开环传递函数写成典型环节乘积的形式; 2. 如果存在交接频率,在ω轴上标出交接频率的坐标位置; 3. 由各典型环节的对数幅频特性叠加后得到系统开环对数幅 频特性的渐近线; 4. 修正误差,画出比较精确的对数幅频特性; 5. 画出各串联典型环节相频特性,将它们相加后得到系统开 环相频特性。 二、绘制系统开环频率特性---伯德图(Bode)的步骤

例4-1已知系统的开环传递函数为 G(s)H(s)=K· (T>T) Ts+1 Ts+1 它由一个放大环节和两个惯性环节串联而成,其对应的 频率特性是 G(j@)H(jo)=K.- jTo+1 jT@+1 幅频特性和相频特性分别为 1 G(jo)H(jo)=K.- T202+1 T202+1 LG(j@)H(jw)--arctgTo-arctgT:0--arctgT (Ti+T2)0 4
4 例4-1 已知系统的开环传递函数为 它由一个放大环节和两个惯性环节串联而成,其对应的 频率特性是 幅频特性和相频特性分别为 1 1 1 1 ( ) ( ) 1 2 + + = j T j T G j H j K 1 1 1 1 ( ) ( ) 2 2 2 2 2 1 + + = T T G j H j K 2 1 2 1 2 1 2 1 ( ) ( ) ( ) T T T T G j H j arctgT arctgT arctg − + = − − = − ( ) 1 1 1 1 ( ) ( ) 1 2 1 2 T T T s T s G s H s K + + =

(1)极坐标图 当0=0时,lG(jo)H(jo)=K,∠G(jo)H(jo)=0° 当D= √TT3 时G(Jo)HUo=K,YT西 ,∠G(jo)H(jo)=-90° T+T 当0=∞时, [G] G(jo)H(jo)=0,∠G(Uo)H(jo=-180° 0=0 K 当o由零增至无穷大时,幅值由K衰减 0 0=0 至零,相角0变至-180°,且均为负相 角。频率特性与负虚轴的交点频率为 -k☑ T+T2 元,交点坐标是(0-k亚)。a T+T 其极坐标图如图4-24所示。 图4-24 开环系统极坐标图 5
5 (1)极坐标图 当 时, 当 时, 当 时, 。 当ω由零增至无穷大时,幅值由K衰减 至零,相角0 0变至-1800 ,且均为负相 角。频率特性与负虚轴的交点频率为 ,交点坐标是 。 其极坐标图如图4-24所示。 = 0 = 0 G( j)H( j) = 0,G( j)H( j) = −180 1 2 1 T T (0, ) 1 2 1 2 T T T T jK + − 0 1 2 1 2 ( ) ( ) ( ) ( ) = −90 + = G j H j T T TT G j H j K , 1 2 1 T T = 0 G( j)H( j) = K,G( j)H( j) = 0 = 0 = 0 1 2 1 2 T T TT jk + − 1 2 1 TT = m I K Re 图4-24 开环系统极坐标图 [G]
(2)伯德图 (a)对数幅频特性 dB L() 由开环传递函数知,对数幅频 A B 20l0g K 渐近特性 特性的渐近线有两个交接频率 无和名,且行,将它们 0 -20dB/dec 1 ō 在o轴上标出(图4-25); T 在纵坐标上找到201gK的点A, 精确特性 40dB/dec 过A点作平行于横轴的直线AB,这 条平行线对应放大环节的幅频特 D 度1 () 性; 0 在交接频率方处作0轴的垂线 (2) (3 -459 (虚线)交平行线AB于B点,以B 为起点作斜率为-20dB/dec的斜 线BC,C点对应交接频率元,折线 ×(4) ABC对应放大环节K和惯性环节 1 的叠加; 图4-25开环系统Bode图 Ts+1 6
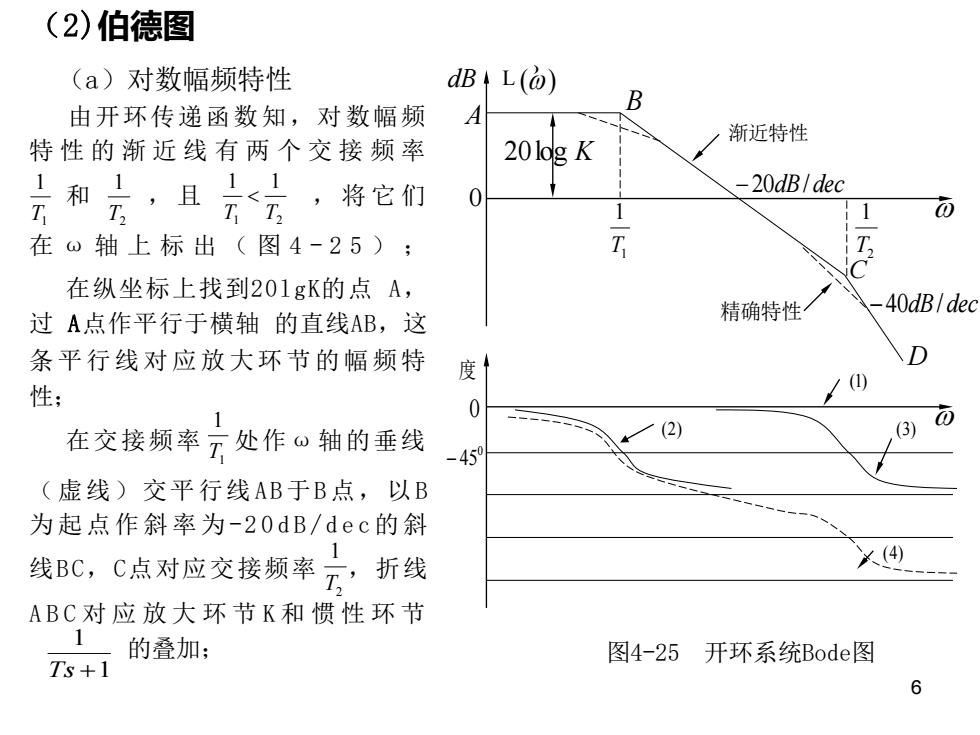
6 (2)伯德图 (a)对数幅频特性 由开环传递函数知,对数幅频 特 性 的 渐 近 线 有 两 个 交 接 频 率 和 , 且 , 将它们 在 ω 轴上标出 ( 图 4 - 2 5 ) ; 在纵坐标上找到20lgK的点 A, 过 A点作平行于横轴 的直线AB,这 条平行线对应放大环节的幅频特 性; 在交接频率 处作ω 轴的垂线 (虚线)交平行线 A B 于B 点, 以B 为起点作斜率为-2 0 d B / d e c 的斜 线B C,C点对应交接频率 ,折线 ABC 对 应 放 大 环 节 K 和 惯 性 环 节 的叠加; 1 2 1 1 T T 1 1 T 2 1 T 1 1 Ts + 1 1 T 2 1 T 图4-25 开环系统Bode图 dBA 0 20log K B −20dB/ dec C 渐近特性 D L() 1 1 T 精确特性 2 1 T −40dB/ dec 度 0 − 450 L () (4) (2) (1) (3)

以C为起点,作斜率为-40dB/dec的斜线CD,折线ABCD即为系统开环对 数幅频特性的渐近线。 (b)对数相频特性 在图4-25上分别画出三个环节的相频特性曲(图中(1)-放大环节, (2)-惯性环节1和(3)-惯性环节2),然后将它们在纵轴方向上相加 得到系统开环相频特性曲线(4)。 例4-2试绘制传递函数为 G(s)= Kv (4-93) S G2(s)= 2 (4-94) 的对数幅频特性
7 以C为起点,作斜率为-40dB/dec的斜线CD,折线ABCD即为系统开环对 数幅频特性的渐近线。 (b)对数相频特性 在图4-25上分别画出三个环节的相频特性曲(图中(1)-放大环节, (2)-惯性环节1和(3)-惯性环节2) ,然后将它们在纵轴方向上相加 得到系统开环相频特性曲线(4)。 例4-2 试绘制传递函数为 (4-93) (4-94) 的对数幅频特性。 s K G s V 1 ( ) = 2 2 ( ) s K G s a =

解:由前面介绍的积分环节的对数幅频特性知,当有个积分环节串联时, 对数幅频特性应是一条过横轴上o=1且斜率为-n×20dB/dec的直线。 式4-93)和(4-94)中分别含有一个和两个积分环节(串联),当 不考虑K和K的影响时,它们的对数幅频特性应是过o=1且斜率分别 为-0dB/dec和-40dB/dec的直线,如图4-26和图4-27中虚线所示。考虑 到K和K的作,上述两条直线应分别在纵轴方向上平移201gK和201gK。 分贝(如图中实线所示),即o=1所对应的坐标值应分别为201gK和 201gK分贝。设对数幅频特性与零分贝线(横轴)的交点频率值分别 为o和⊙a,则有 201gG,0)-a,=201g =20lgK,-20g0,=0(4-95) 20e.Ua)=20e =20gK。-20go2=0(4-96) 8
8 解: 由前面介绍的积分环节的对数幅频特性知,当有n个积分环节串联时, 对数幅频特性应是一条过横轴上ω=1且斜率为 -n×20dB/dec的直线。 式4-93)和( 4-94 )中分别含有一个和两个积分环节(串联),当 不考虑KV和Ka的影响时,它们的对数幅频特性应是过ω=1 且斜率分别 为-0dB/dec和-40dB/dec的直线,如图4-26和图4-27中虚线所示。考虑 到KV和Ka的作,上述两条直线应分别在纵轴方向上平移20lgKv和20lgKa 分贝(如图中实线所示 ),即ω=1所对应的坐标值应分别为20lgKv和 20lgKa分贝。设对数幅频特性与零分贝线(横轴)的交点频率值分别 为ω v和ω a,则有 (4-95) 和 (4-96) 20lg ( ) 20lg 20lg 20lg 0 1 = = − = = = v v v K j K G j v v 20lg ( ) 20lg 20lg 20lg 0 2 2 2 = = − = = = a a a K K G j a a
由上面两式分别得到 O,=K (4-97) Da=√Ka或Ka=D (4-98) 通过上面的分析,在绘制传递函数为式(4-93)和(4-94) 的对数幅频特 性时,可用下述两种方法之一进行。 dB dB a A -20dB/dec 20ogK。 40dB/dec 0, 图4-26 K,与0v的关系 图4-27 K。与0的关系 9
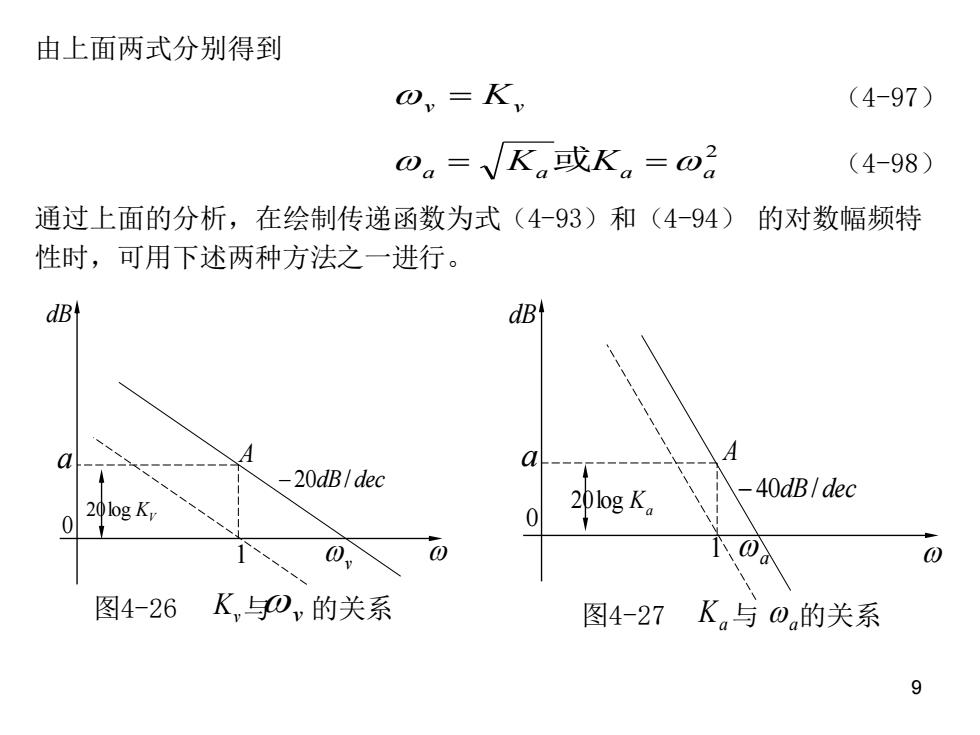
9 由上面两式分别得到 (4-97) (4-98) 通过上面的分析,在绘制传递函数为式(4-93)和(4-94) 的对数幅频特 性时,可用下述两种方法之一进行。 v = Kv 2 a = Ka 或Ka =a KV 20log dB 1 v −20dB/ dec A 0 a 图4-26 K v 与 v 的关系 Ka 20log dB 1 a −40dB/ dec A 0 a 图4-27 Ka 与 a 的关系

方法一:对于式(4-93),先过横轴上ω=1点作横轴的 垂直线,过纵轴上201gK点作横轴的平行线,这两条直线交 于A点,然后过A点作斜率为-20dB/dec的直线即为所求的对 数幅频特性(图4-26);对于式(4-94),过横轴上w=1 点作横轴的垂线过纵轴上201gK。点作横轴的平行线,这两条 直线交于A点,然后过A点作斜率为-40dB/dec的直线即为所求 的对数幅频特性(图4-27)。 方法二:对于式(4-93),先根据式(4-97)在横轴上 找到频率为ωv点,过该点作斜率为-20dB/dec的直线即为所 求的对数幅频特性(图4-26);对于式(4-94),根据式 (4-98)在横轴上找到频率为ω的点,过该点作斜率为 40dB/dec的直线即为所求的对数幅频特性(图4-27)。 10
10 方法一:对于式(4-93),先过横轴上ω=1点作横轴的 垂直线,过纵轴上20lgKv点作横轴的平行线,这两条直线交 于A点,然后过A点作斜率为 -20dB/dec的直线即为所求的对 数幅频特性(图4-26);对于式( 4-94),过横轴上ω=1 点作横轴的垂线过纵轴上20lgKa 点作横轴的平行线,这两条 直线交于A点,然后过A点作斜率为-40dB/dec的直线即为所求 的对数幅频特性(图4-27)。 方法二:对于式(4-93),先根据式(4-97)在横轴上 找到频率为ωV点,过该点作斜率为-20dB/dec的直线即为所 求的对数幅频特性(图4-26);对于式(4-94), 根据式 (4-98)在横轴上找到频率为ω a的点,过该点作斜率为- 40dB/dec的直线即为所求的对数幅频特性(图4-27)