
第三节劳斯-霍尔维茨稳定性判据 稳定性是控制系统最重要的问题,也是对系统最基本 的要求。控制系统在实际运行中,总会受到外界和内部一 些因素的扰动,例如负载或能源的波动、环境条件的改变、 系统参数的变化等。如果系统不稳定,当它受到扰动时, 系统中各物理量就会偏离其平衡工作点,并随时间推移而 发散,即使扰动消失了,也不可能恢复原来的平衡状态。 因此,如何分析系统的稳定性并提出保证系统稳定的措施, 是控制理论的基本任务之一
第三节 劳斯-霍尔维茨稳定性判据 稳定性是控制系统最重要的问题,也是对系统最基本 的要求。控制系统在实际运行中,总会受到外界和内部一 些因素的扰动,例如负载或能源的波动、环境条件的改变、 系统参数的变化等。如果系统不稳定,当它受到扰动时, 系统中各物理量就会偏离其平衡工作点,并随时间推移而 发散,即使扰动消失了,也不可能恢复原来的平衡状态。 因此,如何分析系统的稳定性并提出保证系统稳定的措施, 是控制理论的基本任务之一

常用的稳定性分析方法有: 1.劳斯一赫尔维茨(Routh一Hurwitz)判据:这是一种 代数判据。它是根据系统特征方程式来判断特征根在S平 面的位置,来判断系统的稳定性 2.根轨迹法:这是一种利用图解来系统特征根的方法。 它是以系统开环传递函数的某一参数为变量化出闭环系统 的特征根在S平面的轨迹,从而全面了解闭环系统特征根 随该参数的变化情况。 3.奈魁斯特(Nyquist)判据:这是一种在复变函数理论 基础上建立起来的方法。它根据系统的开环频率特性确定 闭环系统的稳定性,同样避免了求解闭环系统特征根的困 难。这一方法在工程上是得到了比较广泛的应用。 4.李雅普诺夫方法上述几种方法主要适用于线性系统, 而李雅普诺夫方法不仅适用于线性系统,也适用于非线性 系统。该方法是根据李雅普诺夫函数的特征来决定系统的 稳定性
常用的稳定性分析方法有: 1. 劳斯-赫尔维茨(Routh-Hurwitz)判据:这是一种 代数判据。它是根据系统特征方程式来判断特征根在S平 面的位置,来判断系统的稳定性. 2. 根轨迹法:这是一种利用图解来系统特征根的方法。 它是以系统开环传递函数的某一参数为变量化出闭环系统 的特征根在S平面的轨迹,从而全面了解闭环系统特征根 随该参数的变化情况。 3. 奈魁斯特(Nyquist)判据:这是一种在复变函数理论 基础上建立起来的方法。它根据系统的开环频率特性确定 闭环系统的稳定性,同样避免了求解闭环系统特征根的困 难。这一方法在工程上是得到了比较广泛的应用。 4. 李雅普诺夫方法 上述几种方法主要适用于线性系统, 而李雅普诺夫方法不仅适用于线性系统,也适用于非线性 系统。该方法是根据李雅普诺夫函数的特征来决定系统的 稳定性
一、稳定性的概念 稳定性的概念可以通过图3-31所示的方法加以说明。 考虑置于水平面上的圆锥体,其底部朝下时,我们施加一 个很小的外力(扰动),圆锥体会稍微产生倾斜,外作用 力撤消后,经过若干次摆动,它仍会返回到原来的状态。 而当圆锥体尖部朝下放置时,由于只有一点能使圆锥体保 持平衡,所以在受到任何极微小的外力(扰动)后,它就 会倾倒,如果没有外力作用,就再也不能回到原来的状态。 (a)稳定的 (b)不稳定的 图3-31圆锥体的稳定性
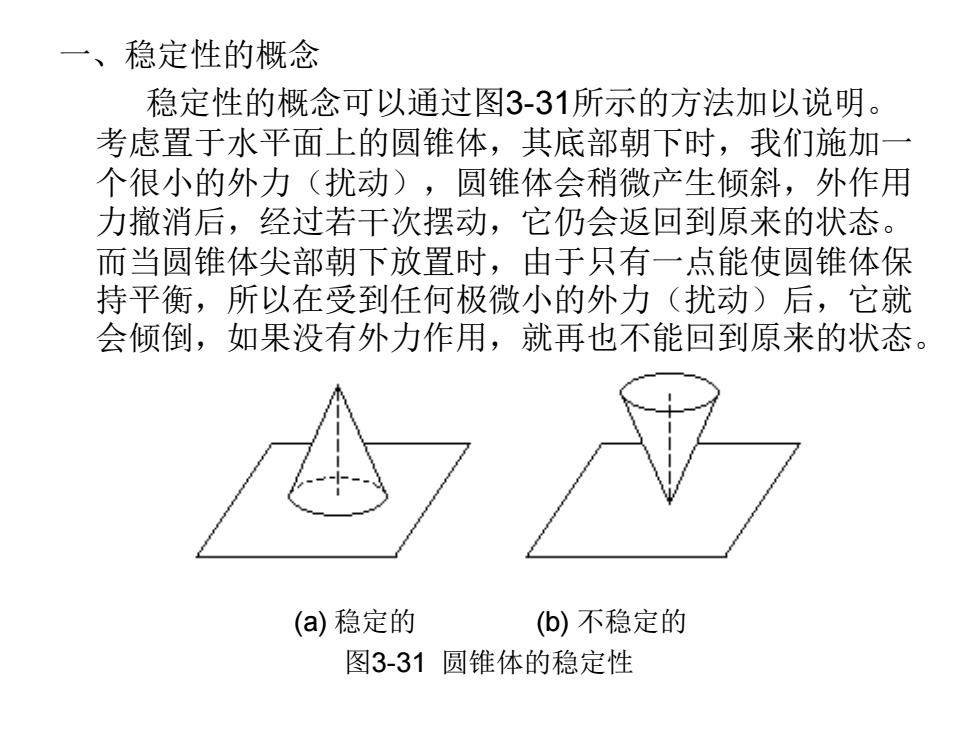
一、稳定性的概念 稳定性的概念可以通过图3-31所示的方法加以说明。 考虑置于水平面上的圆锥体,其底部朝下时,我们施加一 个很小的外力(扰动),圆锥体会稍微产生倾斜,外作用 力撤消后,经过若干次摆动,它仍会返回到原来的状态。 而当圆锥体尖部朝下放置时,由于只有一点能使圆锥体保 持平衡,所以在受到任何极微小的外力(扰动)后,它就 会倾倒,如果没有外力作用,就再也不能回到原来的状态。 (a) 稳定的 (b) 不稳定的 图3-31 圆锥体的稳定性

因此,系统的稳定性定义为,系统在受到外作用力后, 偏离了最初的工作点,而当外作用力消失后,系统能够返 回到原来的工作点,则称系统是稳定的。 设系统在初始条件为零时,在单位理想脉冲作用下, 这时系统的脉冲响应为C()。若t→∞时,脉冲响应 limc() t>○ 这时,线性系统是稳定的。 设系统的特征方程D(S)=0的根为S,由于单位脉冲传 递函数的拉氏变换为1,系统输出的拉式变换为: C(s)=Gp(s)R(s) (s-2,) M(s) C(S)= D(s) ES-S (s-s,)Π(s2+25kws+w)
因此,系统的稳定性定义为,系统在受到外作用力后, 偏离了最初的工作点,而当外作用力消失后,系统能够返 回到原来的工作点,则称系统是稳定的。 设系统在初始条件为零时,在单位理想脉冲作用下, 这时系统的脉冲响应为c(t)。若t →∞时,脉冲响应 这时,线性系统是稳定的。 设系统的特征方程D(s)=0的根为si,由于单位脉冲传 递函数的拉氏变换为1,系统输出的拉式变换为: lim ( ) t c t → == 0 1 1 2 2 1 1 ( ) ( ) ( ) ( ) ( ) ( 2 ) m n i i i q r i i j k k k j k K s z M s A C s D s s s s s s w s w = = = = − = = = − − + + ( ) ( ) ( ) C s G s R s = B

C()=∑Ae+∑B.cos[(wV1-S)] 2-w sinf(Wk -5)t] 瞬态响应项表现为衰减、临界和发散三种情况之一,它是决定系 统稳定性的关键。由于输入量只影响到稳态响应,并且两者具有相 同的特性,即如果输入量)是有界的: |r(t)Koo,t≥0 则稳态响应也必定是有界的。则系统稳定性可以归结为,系统在 任何一个有界输入的作用下,其输出是否有界的问题。 一个稳定的系统定义为,在有界输入的作用下,其输 出响应也是有界的。这叫做有界输入有界输出稳定,又 简称为BIBO稳定
瞬态响应项表现为衰减、临界和发散三种情况之一,它是决定系 统稳定性的关键。由于输入量只影响到稳态响应,并且两者具有相 同的特性,即如果输入量r(t)是有界的: | r(t)|<∞, t ≥0 则稳态响应也必定是有界的。则系统稳定性可以归结为,系统在 任何一个有界输入的作用下,其输出是否有界的问题。 一个稳定的系统定义为,在有界输入的作用下,其输 出响应也是有界的。这叫做有界输入有界输出稳定,又 简称为BIBO稳定。 2 1 1 2 2 1 ( ) cos[( 1 ) ] sin[( 1 ) ] 1 i k k k k n r s t w t i k k k i k r k k k k w t k k k k k C t Ae B e w t C B w e w t w − = = − = = + − − + − −

线性系统的稳定性可以根据闭环极点在S平面内的位置来 确定。设单输入单输出线性系统的微分方程为,即 a,c+a-C+ac+ac (3.58) =+br(m++br+bor 则系统的稳定性由上式左端决定,或者说系统稳定性可 按齐次微分方程式 a,c+a-c++ac+ac=0 (3.59) 来分析。这时,在任何初始条件下,若满足 limc()=lim()==limc()=0 (3.60) >00
线性系统的稳定性可以根据闭环极点在S平面内的位置来 确定。设单输入单输出线性系统的微分方程为,即 (3.58) 则系统的稳定性由上式左端决定,或者说系统稳定性可 按齐次微分方程式 (3.59) 来分析。这时,在任何初始条件下,若满足 (3.60) ( ) ( 1) (1) 1 1 0 ( ) ( 1) (1) 1 1 0 n n n n m m m m a c a c a c a c b r b r b r b r − − − − + + + + = + + + + ( ) ( 1) (1) 1 1 0 n n n n a c a c a c a c − − + + + + = 0 (1) ( 1) lim ( ) lim ( ) lim ( ) n t t t c t c t c t − → → → = = = = 0

则称系统(3.58)是稳定的。 为了决定系统的稳定性,可求出式3.59)的解。由数学 分析知道,式(3.59)的特征方程式为 a,s”+an-++aS+4,=0 (3.61) 设上式有k个实根p,(i=1,2,,k),对共轭复数 根(0,±w)(户1,2,.,),+2r=n,则齐次方程式 (3.59)解的一般式为 c0=∑C,e+∑e/4,+B,sino,) (3.62) 式中系数A,B和C由初始条件决定。 从式(3.62)可知: (1)若卫,<0,-o,<0(即极点都具有负实部),则 式(360)成立,系统最终能恢复至平衡状态,所以系统是 稳定的
则称系统(3.58)是稳定的。 为了决定系统的稳定性,可求出式(3.59)的解。由数学 分析知道,式(3.59)的特征方程式为 (3.61) 设上式有k个实根-pi (i =1,2,…,k),r对共轭复数 根(-σj±jwj ) (j=1,2,…,r),k+2r = n,则齐次方程式 (3.59)解的一般式为 (3.62) 式中系数Aj,Bj和Cj由初始条件决定。 从式(3.62)可知: (1) 若−pi <0,−s j <0 (即极点都具有负实部),则 式(3.60)成立,系统最终能恢复至平衡状态,所以系统是 稳定的。 1 1 ( ) ( cos sin ) j i k r p t t i j j j j i j c t C e e A t B t s − − = = = + + 1 1 1 0 n n n n a s a s a s a − − + + + + = 0

(3)若-p或-o,中有一个或一个以上是正数,则式(3.60) 不满足。当t→o时,c()将发散,系统是不稳定的。 (4)只要-p中有一个为零,或-o,中有一个为零(即有 一对虚根),则式(3.60)不满足。当t→o时,系统输出或 者为一常值,或者为等幅振荡,不能恢复原平衡状态,这 时系统处于稳定的临界状态。 总结上述,可以得出如下结论: 线性系统稳定的充分必要条件 是它的所有特征根均为负实数,或 jg平面 具有负的实数部分。 或它的所有特征根,均 在S平面面的左半部分(见图3-32 图3-32根平面
(3) 若-pi或- s j 中有一个或一个以上是正数,则式(3.60) 不满足。当t→∞时,c(t)将发散,系统是不稳定的。 (4) 只要-pi中有一个为零,或- s j 中有一个为零(即有 一对虚根),则式(3.60)不满足。当t→∞时,系统输出或 者为一常值,或者为等幅振荡,不能恢复原平衡状态,这 时系统处于稳定的临界状态。 总结上述,可以得出如下结论: 线性系统稳定的充分必要条件 是它的所有特征根均为负实数,或 具有负的实数部分。 它的所有特征根,均 在S平面面的左半部分(见图3-32)。 图3-32 根平面

表3.4 系统稳定性的简单例子 系统特征方程及其特征根 极点分布 单位阶跃响应 稳定性 s2+2ga.+02=0 4j四平面 十 512=-w±j0wV1-g9 稳定 (03>-10 ct)=1- 8sin(@+ 1-2 c() +j08平面 8+1=0 稳定 1 5=T c(t)=1-e-ir e(1) s-1=0 jwg平面 不稳定 5-T c)=-1+g2r

表3.4列举了几个简单系统稳定性的例子。需要指出 的是,对于线性定常系统,由于系统特征方程根是由特征 方程的结构(即方程的阶数)和系数决定的,因此系统的 稳定性与输入信号和初始条件无关,仅由系统的结构和参 数决定。 如果系统中每个部分都可用线性定常微分方程描述, 那么,当系统是稳定时,它在大偏差情况下也是稳定的。 如果系统中有的元件或装置是非线性的,但经线性化处理 后可用线性化方程来描述,则当系统稳定时,我们只能说 这个系统在小偏差情况下是稳定的,而在大偏差时不能保 证系统仍是稳定的。 判断系统稳定性的条件是根据系统特征方程的根。但 求解高阶特征方程的根是相当麻烦的,往往需要求助于计 算机。实际上,我们只希望了解特征方程的根在S平面上 分布情况。所以,人们就希望能在不求解特征方程的情况 下,来确定系统的稳定性。下面就介绍常用的劳斯判据和 赫尔维茨判据
表3.4列举了几个简单系统稳定性的例子。需要指出 的是,对于线性定常系统,由于系统特征方程根是由特征 方程的结构(即方程的阶数)和系数决定的,因此系统的 稳定性与输入信号和初始条件无关,仅由系统的结构和参 数决定。 如果系统中每个部分都可用线性定常微分方程描述, 那么,当系统是稳定时,它在大偏差情况下也是稳定的。 如果系统中有的元件或装置是非线性的,但经线性化处理 后可用线性化方程来描述,则当系统稳定时,我们只能说 这个系统在小偏差情况下是稳定的,而在大偏差时不能保 证系统仍是稳定的。 判断系统稳定性的条件是根据系统特征方程的根。但 求解高阶特征方程的根是相当麻烦的,往往需要求助于计 算机。实际上,我们只希望了解特征方程的根在S平面上 分布情况。所以,人们就希望能在不求解特征方程的情况 下,来确定系统的稳定性。下面就介绍常用的劳斯判据和 赫尔维茨判据