
第四章 线性系统的频域分析 频率特性法是经典控制理论中对系统进行 分析与综合的又一重要方法。与时域分析法不 同,频率特性法不是根据系统的闭环极点和零 点来分析系统的时域性能指标,而是根据系统 对正弦信号的稳态响应,即系统的频率特性来 分析系统的频域性能指标。。 频率特性虽然是系统对正弦信号的稳态响 应,但它不仅能反映系统的稳态性能,而且可 以用来研究系统的稳定性和动态性能
1 第四章 线性系统的频域分析 频率特性法是经典控制理论中对系统进行 分析与综合的又一重要方法。与时域分析法不 同,频率特性法不是根据系统的闭环极点和零 点来分析系统的时域性能指标,而是根据系统 对正弦信号的稳态响应,即系统的频率特性来 分析系统的频域性能指标。。 频率特性虽然是系统对正弦信号的稳态响 应,但它不仅能反映系统的稳态性能,而且可 以用来研究系统的稳定性和动态性能

频域性能指标与时域性能指标之间有 着内在的联系。通过这种内在联系,可以 由系统的频域性能指标求出时域性能指标 或反之。因此,频率特性法与时域分析法 是统一的。 应用时域分析法法分析系统时,应先 知道系统的开环传递函数,而频率特性法 既可以根据系统的开环传递函数采用解析 的方法得到系统的频率特性,也可以用实 验方法测出稳定系统或元件的频率特性。 2
2 频域性能指标与时域性能指标之间有 着内在的联系。通过这种内在联系,可以 由系统的频域性能指标求出时域性能指标 或反之。因此,频率特性法与时域分析法 是统一的。 应用时域分析法法分析系统时,应先 知道系统的开环传递函数,而频率特性法 既可以根据系统的开环传递函数采用解析 的方法得到系统的频率特性,也可以用实 验方法测出稳定系统或元件的频率特性

实验法对于那些已经构成系统,但不 知道其内部结构和传递函数的系统,或 难于用分析方法列写动态方程的系统或 环节是很有用的。 本章将介绍频率特性的基本概念, 典型环节和系统的频率特性的极坐标图 (Nyquist)和伯得图(Bode),奈奎斯特 稳定判据和频域性能指标与时域性能指 标之间的关系等。 3
3 实验法对于那些已经构成系统,但不 知道其内部结构和传递函数的系统,或 难于用分析方法列写动态方程的系统或 环节是很有用的。 本章将介绍频率特性的基本概念, 典型环节和系统的频率特性的极坐标图 (Nyquist)和伯得图(Bode),奈奎斯特 稳定判据和频域性能指标与时域性能指 标之间的关系等

§ 4-1 频率特性的概念 § 4-2 典型环节频率特性的绘制 §4-3 系统开环频率特性的绘制 § 4-4 奈奎斯特稳定判据 §4-5控制系统的相对稳定性 4
4 § 4-1 频率特性的概念 § 4-2 典型环节频率特性的绘制 § 4-3 系统开环频率特性的绘制 § 4-4 奈奎斯特稳定判据 § 4-5 控制系统的相对稳定性
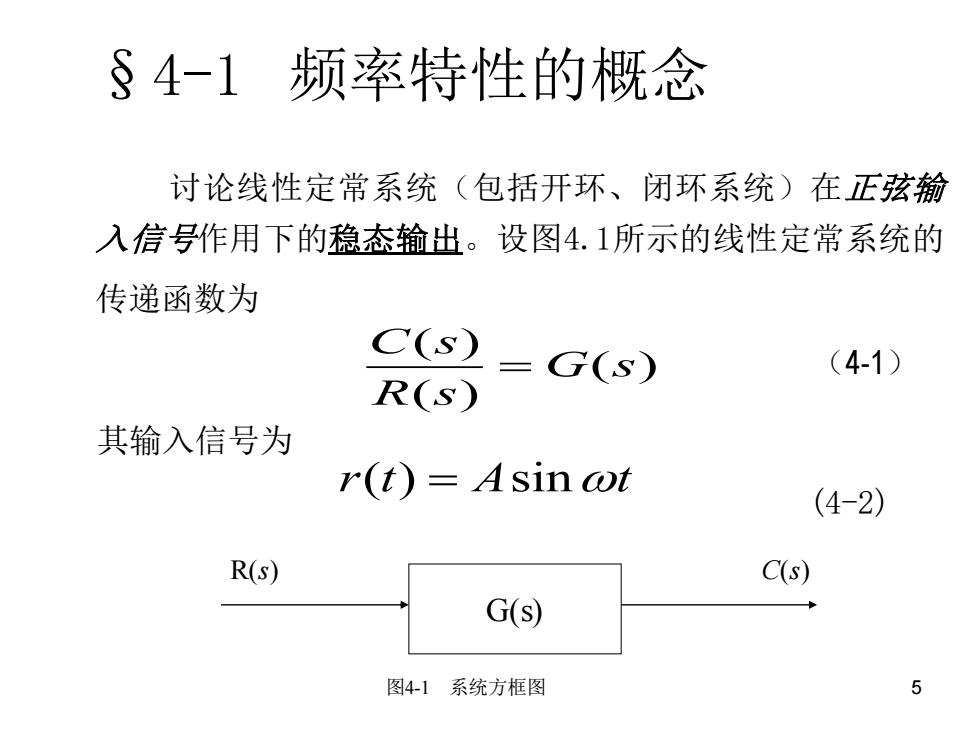
§4-1频率特性的概念 讨论线性定常系统(包括开环、闭环系统)在正弦输 入信号作用下的稳态输出。设图4.1所示的线性定常系统的 传递函数为 C(S) =G(s) (4-1) R(S) 其输入信号为 r(t)=Asin ot (4-2) R(s) C(s) G(s) 图4-1系统方框图 5
5 §4-1 频率特性的概念 讨论线性定常系统(包括开环、闭环系统)在正弦输 入信号作用下的稳态输出。设图4.1所示的线性定常系统的 传递函数为 其输入信号为 (4-2) (4-1) ( ) ( ) ( ) C s G s R s = G(s) R(s) C(s) 图4-1 系统方框图 r t A t ( ) sin =

则输入信号的拉氏变换是 Aw Ao R(S)= 52+02 (s+j0(s-j0) (4-3) 系统的传递函数通常可以写成 M(s) M(s) G(s)= N(s)(s-5)(s-5,)..(s-s,) (4-4) 由此得到输出信号的拉氏变换 C(s)=G(s)R(s) M(s) Aw (s-Ss-52)…(s-5n)(s+j0s-j0) (4-5) b an s+jo s-j@s-S S-S2 S-S 6
6 则输入信号的拉氏变换是 (4-3) 系统的传递函数通常可以写成 (4-4) 由此得到输出信号的拉氏变换 (4-5) 2 2 ( ) ( )( ) A A R s s s j s j = = + + − 1 2 ( ) ( ) ( ) ( ) ( )( ) ( ) n M s M s G s N s s s s s s s = = − − − 1 2 1 2 1 2 ( ) ( ) ( ) ( ) ( )( ) ( ) ( )( ) n n n C s G s R s M s A s s s s s s s j s j b b a a a s j s j s s s s s s = = − − − + − = + + + + + + − − − −

对上式进行拉氏反变换得到系统的输出为 c(t)=be-ioi +beioi +aesv+ (4-6) =a2e+…+ane 对稳定系统,S1心2,,Sn都具有负实部,当时间趋于无穷大时, 上式的暂态分量将衰减至零。因此系统的稳态响应为 c(o)=limc(t)=be jo +bejoor (4-7) 其中待定系数b和万可按下式计算 6=0+g-+m-= Ao G(-j@)A (4-8) 2i b=G(s) s+joXs-jo)(s-ja)- Aw G(j@)A (4-9) 2j 7
7 对上式进行拉氏反变换得到系统的输出为 (4-6) 对稳定系统,s1 ,s2 ,….,sn都具有负实部,当时间t趋于无穷大时, 上式的暂态分量将衰减至零。因此系统的稳态响应为 (4-7) 其中待定系数b和 可按下式计算 (4-8) (4-9) 1 2 1 2 ( ) n j t j t s t s t s t n c t be be a e a e a e − = + + + = + + ( ) lim ( ) j t j t t c c t be be − → = = + ( ) ( ) ( ) ( )( ) 2 s j A G j A b G s s j s j s j j = − − = + = − + − ( ) ( ) ( ) ( )( ) 2 s j A G j A b G s s j s j s j j = − = = + − b

G(o)是一个复数,用模和幅角可表示为 G(j@)=G(j@).eo) (4-10) o)=∠Gjo)-arcts ReGjo)】 ImG(j@) (4-11) 同样,G(@)可以表示为 G(-j@)=G(-j0)-e=G(j@)e) (4-12) 将式(4-8)(4-9)以及式(4-10)(4-12)代入式(4-7)可得 c()=(jo)e)(a)el =G(j@)A. ()-e-jo) (4-13) 2j =G(j@)A.sin(ot+) 8
8 G(jω)是一个复数,用模和幅角可表示为 (4-10) (4-11) 同样, G(-jω)可以表示为 (4-12) 将式(4-8)(4-9)以及式(4-10)(4-12)代入式(4-7)可得 (4-13) ( ) ( ) ( ) j G j = G j e = = Re ( ) Im ( ) ( ) ( ) G j G j G j arctg ( ) ( ) ( ) ( ) ( ) j j G j G j e G j e − − − = − = ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 ( ) 2 ( ) sin( ) j t j t j j j t j t Ae Ae c G j e G j e j j e e G j A j G j A t − − + − + = − + − = = +

或 c(∞)=Csin(ωt+Φ (4-14) 式中C=|G(jo)A为稳态输出信号的幅值。 上式表明,线性定常系统对正弦输入信号的稳态响应仍然 是与正弦输入信号同频率的正弦信号;输出信号的振幅是输入 信号振幅的G(o)倍;输出信号相对输入信号的相移 为中=∠G(o);输出信号的振幅及相移都是角频率o的函数。 我们把 G(jω)=|G(jo)leco) (4-15) 称为系统的频率特性,它反映了在正弦输入信号作用下,系统 的稳态响应与输入正弦信号的关系。 9
9 或 (4-14) 式中 为稳态输出信号的幅值。 上式表明,线性定常系统对正弦输入信号的稳态响应仍然 是与正弦输入信号同频率的正弦信号;输出信号的振幅是输入 信号振幅的 倍;输出信号相对输入信号的相移 为 ;输出信号的振幅及相移都是角频率 的函数。 我们把 (4-15) 称为系统的频率特性,它反映了在正弦输入信号作用下,系统 的稳态响应与输入正弦信号的关系。 c C t ( ) sin( ) = + C G j A = ( ) G( j) = G( j) ( ) ( ) ( ) j G j G j G j e =

其中 IG(jw)-C(@) (4-16) 称为系统的幅频特性,它反映系统在不同频率正弦信号作用下, 输出稳态幅值与输入信号幅值的比值,即系统的放大(或衰减) 特性。 ImG(j@) (o)=∠G(jo)=arctg ReG(j@) (4-17) 称为系统的相频特性,它反映系统在不同频率正弦信号的作用 下,输出信号相对输入信号的相移。系统的幅频特性和相频特 性统称为系统的频率特性。 10
10 其中 (4-16) 称为系统的幅频特性,它反映系统在不同频率正弦信号作用下, 输出稳态幅值与输入信号幅值的比值,即系统的放大(或衰减) 特性。 (4-17) 称为系统的相频特性,它反映系统在不同频率正弦信号的作用 下,输出信号相对输入信号的相移。系统的幅频特性和相频特 性统称为系统的频率特性。 Im ( ) ( ) ( ) Re ( ) G j G j arctg G j = = ( ) ( ) C G j A =