
第五节应用MATLAB分析控制系统 的性能 这一节将说明如何利用MATLAB来分析控制系统。 系统分析的主要内容包括如何抑制干扰、如何减小稳 态误差、如何调节瞬态响应以及如何减少系统对参数 变化的影响等
第五节 应用MATLAB分析控制系统 的性能 这一节将说明如何利用MATLAB来分析控制系统。 系统分析的主要内容包括如何抑制干扰、如何减小稳 态误差、如何调节瞬态响应以及如何减少系统对参数 变化的影响等
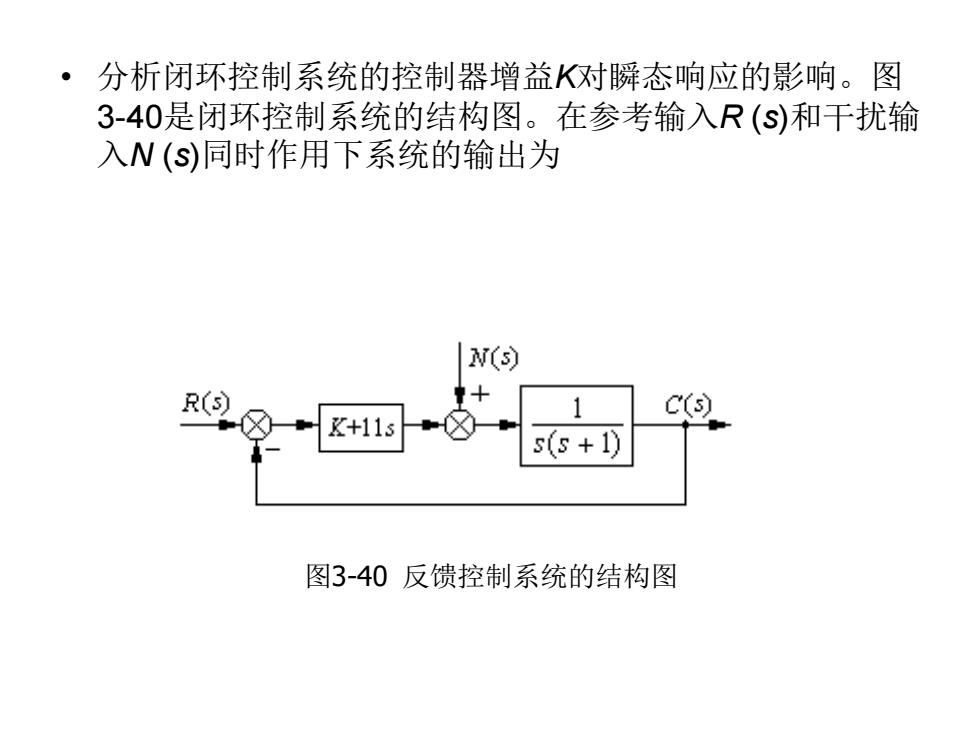
·分析闭环控制系统的控制器增益K对瞬态响应的影响。图 3-40是闭环控制系统的结构图。在参考输入R(S)和干扰输 入N(S)同时作用下系统的输出为 N(s) R(5) 1 K+11s (X 5(S+1) 图3-40反馈控制系统的结构图
• 分析闭环控制系统的控制器增益K对瞬态响应的影响。图 3-40是闭环控制系统的结构图。在参考输入R (s)和干扰输 入N (s)同时作用下系统的输出为 2 2 11 1 ( ) ( ) ( ) 12 12 K s C s R s N s s s K s s K + = + + + + + 图3-40 反馈控制系统的结构图

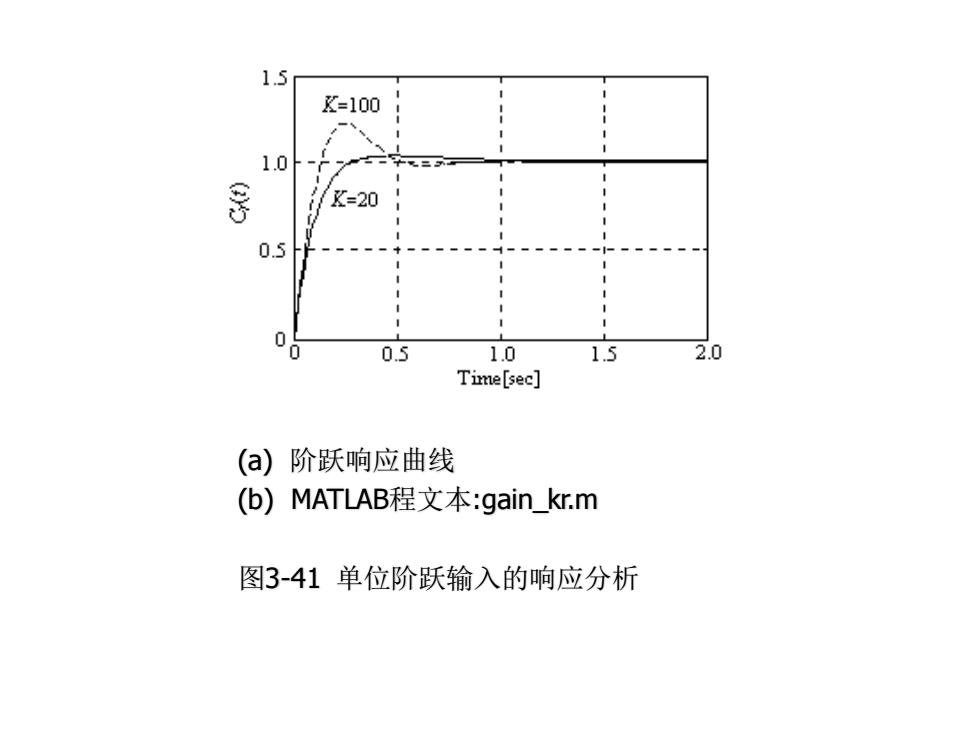
·如果单纯考虑增益K对参考输入产生的瞬态响应的影响, 可以预计增加K将导致超调量增加、调整时间减少和响应 速度提高。在增益K=20和K=100时,系统对参考输入的 单位阶跃响应曲线以及相应的MATLAB程序文本gain kr.m 示于图3-41。对比两条响应曲线,可以看出上述预计的正 确性。 ·尽管在图中不能明显看出增大K能减少调整时间,但是这 一点可以通过观察MATLAB程序的运行数据得以验证。这 个例子说明了控制器增益K是如何改变系统瞬态响应的。 根据以上分析,选择K=20可能是一个比较好的方案。尽 管如此,在做出最后决定之前还应该考虑其他因素
• 如果单纯考虑增益K对参考输入产生的瞬态响应的影响, 可以预计增加K将导致超调量增加、调整时间减少和响应 速度提高。在增益K=20和K=100时,系统对参考输入的 单位阶跃响应曲线以及相应的MATLAB程序文本gain_kr.m 示于图3-41。对比两条响应曲线,可以看出上述预计的正 确性。 • 尽管在图中不能明显看出增大K能减少调整时间,但是这 一点可以通过观察MATLAB程序的运行数据得以验证。这 个例子说明了控制器增益K是如何改变系统瞬态响应的。 根据以上分析,选择K=20可能是一个比较好的方案。尽 管如此,在做出最后决定之前还应该考虑其他因素
1.5 X=100 1.0 X=20 0.5 。◆ 0 0.5 1.0 1.5 2.0 Time [sec] (a)阶跃响应曲线 (b)MATLAB程文本:gain_kr.m 图3-41单位阶跃输入的响应分析
(a) 阶跃响应曲线 (b) MATLAB程文本:gain_kr.m 图3-41 单位阶跃输入的响应分析

%K=20和K=100时,参考输入的单位阶跃响应:gain kr..m numg=[1];deng=[110]; K1=100;K2=20; num1=[11K1];num2=[11K2];den=[01]; %简化结构图 [na,da]=series(num1,den,numg,deng); [nb,db]=series(num2,den,numg,deng); [numa,dena]=cloop(na,da); [numb,denb]=cloop(nb,db); %选择时间间隔 t=[0:0.01:2.0] [c1,x,t]=step(numa,dena,t); [c2,x,t]=step(numb,denb,t); plot(t,c1,'--',t,c2) xlabel('Time[sec]),ylabel('Cr(t)),grid
% K=20和K=100时,参考输入的单位阶跃响应:gain_kr.m numg=[1];deng=[1 1 0]; K1=100;K2=20; num1=[11 K1];num2=[11 K2];den=[0 1]; %简化结构图 [na,da]=series(num1,den,numg,deng); [nb,db]=series(num2,den,numg,deng); [numa,dena]=cloop(na,da); [numb,denb]=cloop(nb,db); %选择时间间隔 t=[0:0.01:2.0]; [c1,x,t]=step(numa,dena,t); [c2,x,t]=step(numb,denb,t); plot(t,c1,'--',t,c2) xlabel('Time[sec]'),ylabel('Cr(t)'),grid

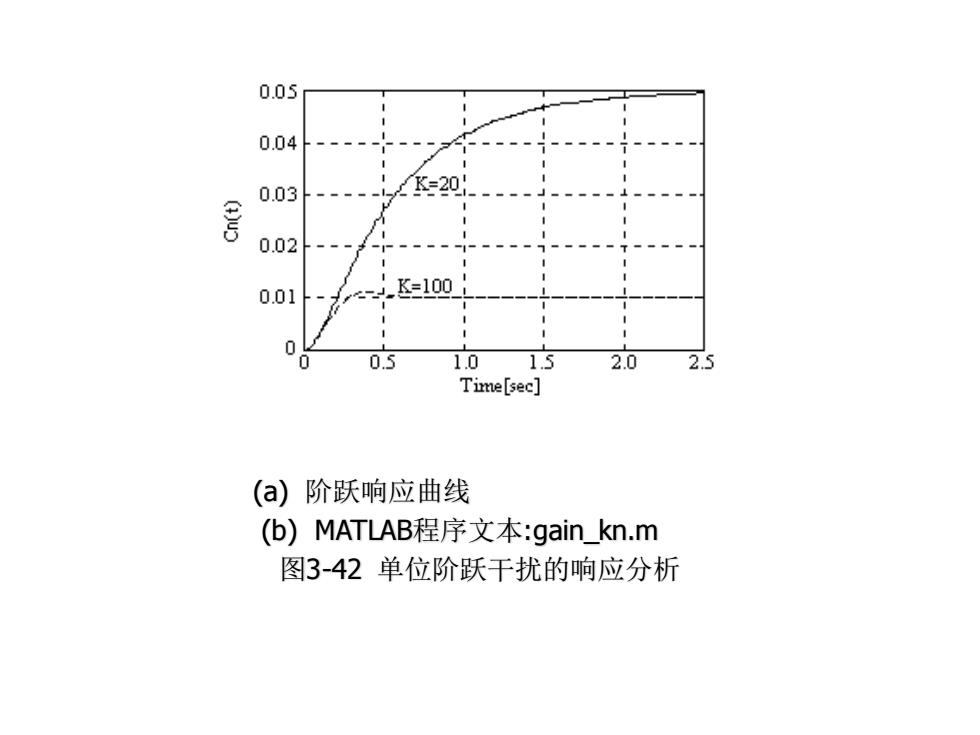
·在对K做出最后选择之前,非常重要的是要研究系统对单 位阶跃干扰的响应,有关结果和相应的MATLAB程序文本 如图3-42所示。从中可以看到,增加K减少了单位干扰响 应的幅值。对于K=20和K=100,响应的稳态值分别为0.05 和0.01。对干扰输入的稳态值可按终值定理求得 如果仅从抗干扰的角度考虑,选择K=100更合适。 在本例中所求出的稳态误差、超调量和调整时间(2% 误差)归纳于表3.7
• 在对K做出最后选择之前,非常重要的是要研究系统对单 位阶跃干扰的响应,有关结果和相应的MATLAB程序文本 如图3-42所示。从中可以看到,增加K减少了单位干扰响 应的幅值。对于K=20和K=100,响应的稳态值分别为0.05 和0.01。对干扰输入的稳态值可按终值定理求得 如果仅从抗干扰的角度考虑,选择K=100更合适。 在本例中所求出的稳态误差、超调量和调整时间(2% 误差)归纳于表3.7。 0 1 1 1 lim ( ) lim { } ( 12) t s c t s → → s s K s K = = + +
0.05 0.04 0.03 -K=20 0.02 0.01 K100 0 0 0.5 1.0 1.5 2.0 2.5 Time[sec] (a)阶跃响应曲线 (b)MATLAB程序文本:gain_kn.m 图3-42单位阶跃干扰的响应分析
(a) 阶跃响应曲线 (b) MATLAB程序文本:gain_kn.m 图3-42 单位阶跃干扰的响应分析

%K=20和K=100时,干扰输入的单位阶跃响应:gain_kn.m numg=[1];deng=[110]; ·K1=100;K2=20; 。 num1=[11K1];num2=[11K2]den=[01]: ·%简化结构图 [numa,dena]=feedback(numg,deng,num1,den); 。 [numb,denb]=feedback(numg,deng,num2,den); ·%选择时间间隔 t=[0:0.01:2.5]; [c1,x,t]=step(numa,dena,t); [c2,x,t]=step(numb,denb,t); ·plot(t,c1,'-',t,c2) xlabel('Time[sec]),ylabel(Cn(t)),grid
• % K=20和K=100时,干扰输入的单位阶跃响应:gain_kn.m • numg=[1];deng=[1 1 0]; • K1=100;K2=20; • num1=[11 K1];num2=[11 K2];den=[0 1]; • %简化结构图 • [numa,dena]=feedback(numg,deng,num1,den); • [numb,denb]=feedback(numg,deng,num2,den); • %选择时间间隔 • t=[0:0.01:2.5]; • [c1,x,t]=step(numa,dena,t); • [c2,x,t]=step(numb,denb,t); • plot(t,c1,'--',t,c2) • xlabel('Time[sec]'),ylabel('Cn(t)'),grid

表3.7 K=20和K=100时,控制系统的响应特性 K值 K=20 K=100 超调量σ,% 4% 22% 调整时间t, 1.0秒 0.7秒 稳态误差es 5% 1%
表3.7 K=20和K=100时,控制系统的响应特性 K值 K=20 K=100 超调量sp% 4% 22% 调整时间 t s 1.0秒 0.7秒 稳态误差ess 5% 1%

小结 。 本章对控制系统分析的基本内容进行了讨论,概括地讲, 就是稳定性、瞬态性能和稳态性能。 ·使用闭环反馈,必然带来设备及元器件的花销和随之而来 的系统复杂问题,另外,对于原本稳定的开环系统,由于 反馈的引入,完全可以造成闭环系统的不稳定。但是,尽 管如此,反馈控制系统在各行各业得到了广泛的应用,这 是由于反馈控制能够: (1)减少被控过程G($)中参数变化时系统的灵敏度; (2)有利于控制和调节系统的瞬态响应性能: (3)提高系统对干扰的抑制力; (4)减小或消除系统的静态误差
小结 • 本章对控制系统分析的基本内容进行了讨论,概括地讲, 就是稳定性、瞬态性能和稳态性能。 • 使用闭环反馈,必然带来设备及元器件的花销和随之而来 的系统复杂问题,另外,对于原本稳定的开环系统,由于 反馈的引入,完全可以造成闭环系统的不稳定。但是,尽 管如此,反馈控制系统在各行各业得到了广泛的应用,这 是由于反馈控制能够: (1)减少被控过程G(s)中参数变化时系统的灵敏度; (2)有利于控制和调节系统的瞬态响应性能; (3)提高系统对干扰的抑制力; (4)减小或消除系统的静态误差