
第六章 根轨迹法 ·§6-1根轨迹的概念 ·§6-2绘制根轨迹的规则 ·§6-3广义根轨迹 ·§6-4系统性能分析 7
1 第六章 根轨迹法 • §6–1 根轨迹的概念 • §6–2 绘制根轨迹的规则 • §6–3 广义根轨迹 • §6–4 系统性能分析

根轨迹法是一种图解方法,它是古典控制理 论中对系统进行分析和综合的基本方法之一。由 于根轨迹图直观地描述了系统特征方程的根(即 系统的闭环极点)在S平面上的分布,因此,用根 轨迹法分析控制系统十分方便,特别是对于高阶 系统和多回路系统,应用根轨迹法比用其他方法 更为方便,因此在工程实践中获得了广泛应用。 本章主要介绍根轨迹的概念,绘制根轨迹的 基本规则和用根轨迹法分析自动控制系统的方法。 2
2 根轨迹法是一种图解方法,它是古典控制理 论中对系统进行分析和综合的基本方法之一。由 于根轨迹图直观地描述了系统特征方程的根(即 系统的闭环极点)在S平面上的分布,因此,用根 轨迹法分析控制系统十分方便,特别是对于高阶 系统和多回路系统,应用根轨迹法比用其他方法 更为方便,因此在工程实践中获得了广泛应用。 本章主要介绍根轨迹的概念,绘制根轨迹的 基本规则和用根轨迹法分析自动控制系统的方法

§6-1根轨迹的概念 一、根轨迹图 根轨迹图是开环系统某一参数由零变化到无 穷时,闭环系统特征方程的根(即闭环极点)在 S平面上的变化轨迹。 例6-1 已知单位负反馈系统的开环传递函数为 G(s)H(s)=- K (s+2) 试分析该系统的特征方程的根随系统参数K的变 化在S平面上的分布情况。 3
3 §6–1 根轨迹的概念 一﹑根轨迹图 根轨迹图是开环系统某一参数由零变化到无 穷时,闭环系统特征方程的根(即闭环极点)在 S平面上的变化轨迹。 例6-1 已知单位负反馈系统的开环传递函数为 试分析该系统的特征方程的根随系统参数 的变 化在S平面上的分布情况。 s(s 2) K G(s) H( ) + = r s Kr

解 系统的闭环传递函数 φ(S)= C(s) G(s) K R(s) 1+G(s)H(s) s2+2S+K 系统的特征方程为 s2+2s+K,=0 特征方程的根是 S1=-1+V1-K,S2=-1-V1-K, 设K,∈(0,∞), 当K,=0时,S1=0,S2=-2 ; 当0<K,<1时,S,与S2为不相等的两个负实根; 当K,=1时,S1=S2=-1为等实根: 4
4 解 系统的闭环传递函数 系统的特征方程为 特征方程的根是 设 〔0, ∞﹚, 当 时, ; 当 时, 与 为不相等的两个负实根; 当 时, 为等实根; r 2 r s 2s K K 1 G(s)H(s) G(s) R(s) C(s) (s) + + = + = = s 2s Kr 0 2 + + = 1 r 2 1 1 Kr s = −1+ 1− K ,s = − − − K r = 0 K r 0 1 K r s1 = 0,s2 = −2 1 s 2 s 1 K r = s1 = s2 = −1

当1<K,<w时,S2=-1±jVK,-1为一对共 轭复根,其实部都等于-1,虚部随K,值的增加 而增加; 当K→∞时,S1、S2的实部都等于-1,是常 数,虚部趋向无穷远处。 该系统特征方程的根随开环系统参数从零变到 无穷时在S平面上变化的轨迹如图6-1所示。 5
5 当 时, 为一对共 轭复根,其实部都等于-1,虚部随 值的增加 而增加; 当 →∞时, 、 的实部都等于-1,是常 数,虚部趋向无穷远处 。 Kr 1 K r 1 s 2 s s 1 K 1 1,2 = − j r − Kr 该系统特征方程的根随开环系统参数从零变到 无穷时在S平面上变化的轨迹如图6-1所示

↑jω ↑K,→0 [s] P(K=0) (K,=1) P(K,=0) 之 一1 0 ↓K,→0 图6-1例6-1的根轨迹 6
6 j -2 -1 0 Kr → Kr → ( 0) P1 Kr = ( 0) (Kr =1) P2 Kr = [s] 图 6 -1 例 6 - 1的根轨迹

当系统参数K为某一确定的值时,闭环系 统特征方程的根在$平面上变化的位置便可确定, 由此可进一步分析系统的性能。值的变化对闭 环系统特征方程的影响可在根轨迹上直观地看到, 因此系统参数对系统性能的影响也一目了然。所 以用根轨迹图来分析自动控制系统是十分方便的。 上例中,根轨迹图是用解析法作出的,这对于二 阶系统并非难事,但对于高阶系统,求解特征方 程的根就比较困难了。 如果要研究系统参数的变化对闭环系统特征 方程根的影响,需要大量反复的计算。 1948年伊万斯(WR·EVANS)提出了根轨迹 法。该方法不需要求解闭环系统的特征方程,只 需依据开环传递函数便可会绘制系统的根轨迹图
7 当系统参数 为某一确定的值时,闭环系 统特征方程的根在S平面上变化的位置便可确定, 由此可进一步分析系统的性能。 值的变化对闭 环系统特征方程的影响可在根轨迹上直观地看到, 因此系统参数对系统性能的影响也一目了然。所 以用根轨迹图来分析自动控制系统是十分方便的。 上例中,根轨迹图是用解析法作出的,这对于二 阶系统并非难事,但对于高阶系统,求解特征方 程的根就比较困难了。 如果要研究系统参数的变化对闭环系统特征 方程根的影响,需要大量反复的计算。 1948年伊万斯(W·R·EVANS)提出了根轨迹 法。该方法不需要求解闭环系统的特征方程,只 需依据开环传递函数便可会绘制系统的根轨迹图。 Kr Kr
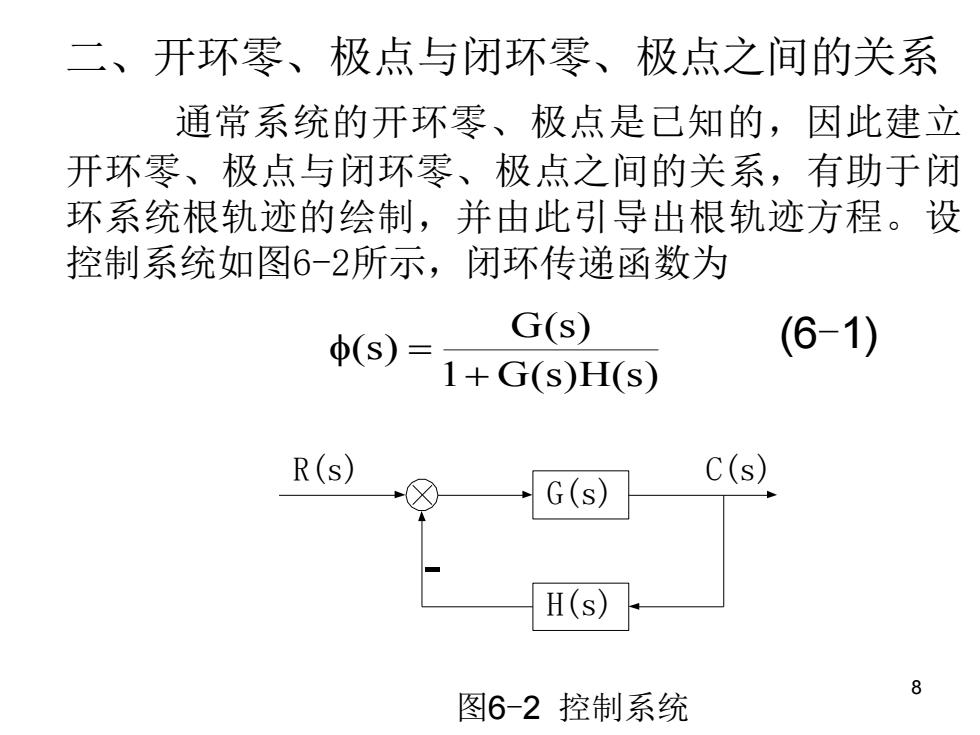
二、开环零、极点与闭环零、极点之间的关系 通常系统的开环零、极点是己知的,因此建立 开环零、极点与闭环零、极点之间的关系,有助于闭 环系统根轨迹的绘制,并由此引导出根轨迹方程。设 控制系统如图6-2所示,闭环传递函数为 G(s) (s)= (6-1) 1+G(s)H(s) R(s) C(s) G(s) H(s 8 图6-2控制系统
8 二、开环零、极点与闭环零、极点之间的关系 通常系统的开环零、极点是已知的,因此建立 开环零、极点与闭环零、极点之间的关系,有助于闭 环系统根轨迹的绘制,并由此引导出根轨迹方程。设 控制系统如图6-2所示,闭环传递函数为 (6-1) - 1 G(s)H(s) G(s) (s) + = G(s) H(s) R(s) C(s) 图6-2 控制系统

前向通路传递函数G(s)和反馈通路传递函数H(s 可分别表示 (s+1) G(s)=K1 j=1 月s-,) (6-2) sv A(Ts+1) "s (s-P) -1 (ts+) H(s)=K2 点(s-乙) 4(Ts+1) (s-B) (6-3) 式中K1为前向通路增益,Kr为前向通路根轨 迹增益;K2为反馈通路增益,K2为反馈通路根轨迹 增益。 9
9 前向通路传递函数G(s)和反馈通路传递函数H(s) 可分别表示 (6-2) (6-3) 式中 为前向通路增益, 为前向通路根轨 迹增益; 为反馈通路增益, 为反馈通路根轨迹 增益。 = = = = − − = + + = q i 1 i f j 1 j q 1r i 1 i f j 1 j 1 s (s P ) (s Z ) K s (Ts 1) ( s 1) G(s) K = = = = − − = + + = h i 1 i l j 1 j h 2r i 1 i l j 1 j 2 (s P ) (s Z ) K (Ts 1) ( s 1) H(s) K K1 K1r K2 K2r

系统的开环传递函数为 (+D (s-Zj) G(s)H(s)=K- =K. i-1 6-4) (Ts+D ss-P K=K1·K2 为系统的开环增益, K,=Kr·K2r为开环系统的根轨迹增益; m=f+L 为开环系统的零点数, n=q+h+v为开环系统的极点数。 将式(6-2)和(6-4)代入(6-1)可得 K(s-Z)(s-P,) φ(S)= s(s-P)+K,(s-Z,) (6-50
10 系统的开环传递函数为 (6-4) 为系统的开环增益, 为开环系统的根轨迹增益; m=f+L 为开环系统的零点数, 为开环系统的极点数。 将式(6-2)和(6-4)代入(6-1)可得 (6-5) − = = − = = − − = + + = n i 1 i m j 1 j n r i 1 i m j 1 j s (s P ) (s Z ) K s (Ts 1) ( s 1) G(s)H(s) K K K1 K2 = n = q + h + = − = = = − + − − − = m j 1 r i n i 1 i h j 1 j f i 1 1r i s (s P ) K (s Z ) K (s Z ) (s P ) (s) K1r K2r = Kr