
第三章控制系统的时域分析法 ·第一节二阶系统的瞬态响应及性能指标 ·第二节增加零极点对二阶系统响应的影响 ·第三节反馈控制系统的稳态误差 ·第四节劳斯-霍尔维茨稳定性判据
第三章 控制系统的时域分析法 • 第一节 二阶系统的瞬态响应及性能指标 • 第二节 增加零极点对二阶系统响应的影响 • 第三节 反馈控制系统的稳态误差 • 第四节 劳斯-霍尔维茨稳定性判据

第一节二阶系统的瞬态响应及性能指标 瞬态响应是指系统的输出从输入信号()作用时刻起, 到稳定状态为止,随时间变化的过程。分析系统的瞬态响应, 可以了解系统的稳态性能(稳定性)和过渡过程的性能。分 析系统的瞬态响应,有以下方法: 1.直接求解法 2.间接评价法 3.计算机仿真法 本小节首先讨论典型输入信号、性能指标等内容,然后 讨论一阶、二阶系统的瞬态响应,最后讨论如何处理高阶系 统的瞬态响应问题
第一节 二阶系统的瞬态响应及性能指标 瞬态响应是指系统的输出从输入信号r(t)作用时刻起, 到稳定状态为止,随时间变化的过程。分析系统的瞬态响应, 可以了解系统的稳态性能(稳定性)和过渡过程的性能。分 析系统的瞬态响应,有以下方法: 1. 直接求解法 2. 间接评价法 3. 计算机仿真法 本小节首先讨论典型输入信号、性能指标等内容,然后 讨论一阶、二阶系统的瞬态响应,最后讨论如何处理高阶系 统的瞬态响应问题

一、典型输入信号 (一)阶跃信号 阶跃信号的表达式为: t>O r() (3.1) t≤O 当A=1时,则称为单位阶跃信号,常用1()表示,如图3-1所 示。 图3-1阶跃信号 图3-2斜坡信号
一、典型输入信号 (一)阶跃信号 阶跃信号的表达式为: 当A=1时,则称为单位阶跃信号,常用1(t)表示,如图3-1所 示。 图3-1 阶跃信号 图3-2 斜坡信号 ( ) (3.1) A t r t t = 0 0 0

(二)斜坡信号 斜坡信号在t=0时为零,并随时间线性增加,所以也叫 速度信号。它等于阶跃信号对时间的积分,而它对时间的 导数就是阶跃信号。斜坡信号的表达式为: t>O (3.2) t≤O
(二)斜坡信号 斜坡信号在t =0时为零,并随时间线性增加,所以也叫 速度信号。它等于阶跃信号对时间的积分,而它对时间的 导数就是阶跃信号。斜坡信号的表达式为: (3.2) = 0 0 0 t At t r t ( )
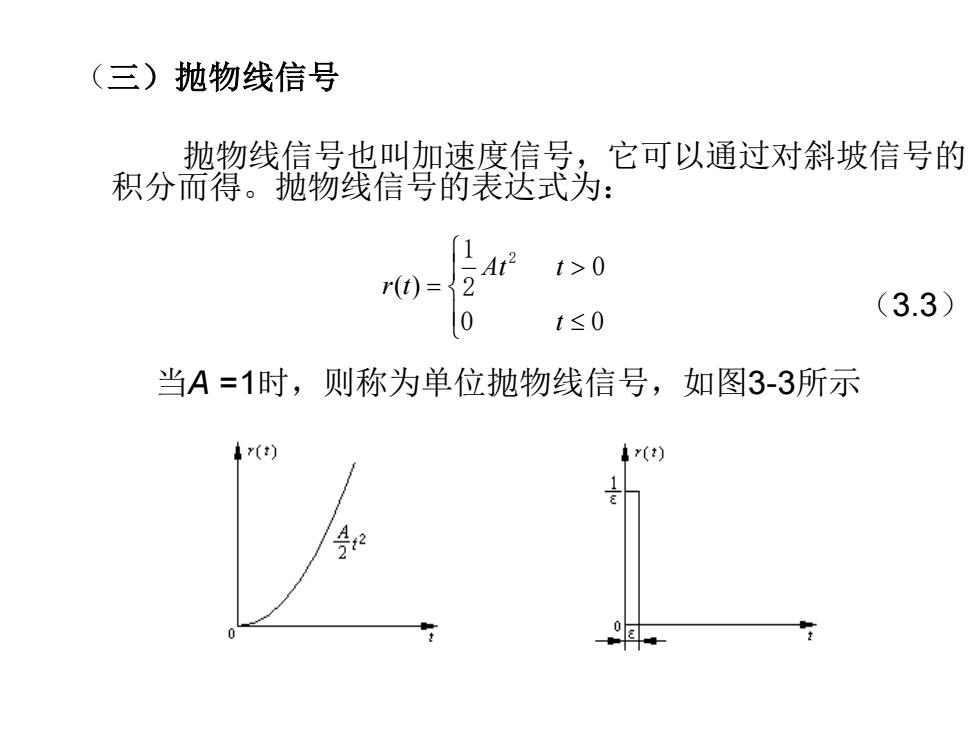
(三)抛物线信号 抛物线信号也叫加速度信号,它可以通过对斜坡信号的 积分而得。抛物线信号的表达式为: t>0 r(t)= (3.3) 0 t≤0 当A=1时,则称为单位抛物线信号,如图3-3所示 (t)
(三)抛物线信号 抛物线信号也叫加速度信号,它可以通过对斜坡信号的 积分而得。抛物线信号的表达式为: (3.3) 当A =1时,则称为单位抛物线信号,如图3-3所示 = 0 0 0 ( ) t At t r t 2 2 1

(四)脉冲信号 单位脉冲信号的表达式为: r()= 0s 其图形如图3-4所示。是一宽度为ε,高度为1/ε的矩形 脉冲,当ε趋于零时就得理想的单位脉冲信号(亦称)函数)。 ()dt =1 (3.5)
(四)脉冲信号 单位脉冲信号的表达式为: (3.4) 其图形如图3-4所示。是一宽度为e ,高度为1/e 的矩形 脉冲,当e 趋于零时就得理想的单位脉冲信号(亦称d(t) 函数)。 (3.5) = e e e t t t r t 0 0及 0 1 ( ) ( )d = 1 − d t t
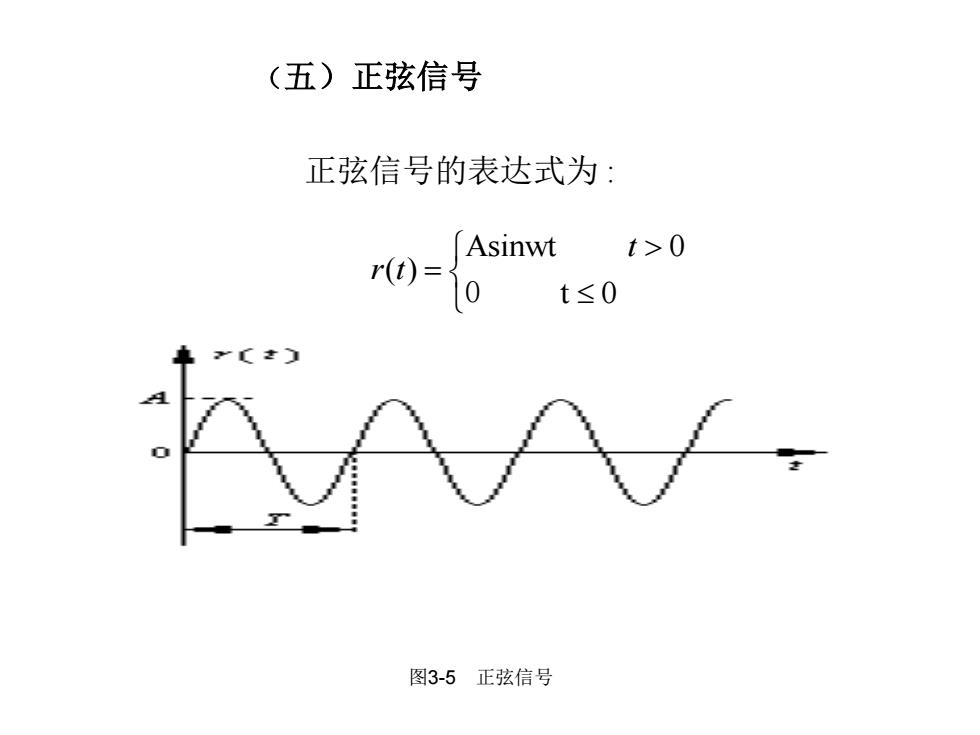
(五)正弦信号 正弦信号的表达式为: Asinwt t>0 r(t) t≤0 图3-5正弦信号
(五)正弦信号 正弦信号的表达式为 : (3.6) 其中A为幅值,w =2p/T为角频率。 图3-5 正弦信号 Asinwt 0 ( ) t 0 t r t = 0

二、系统的性能指标 系统的瞬态性能通常以系统在初始条件为零的情况下, 对单位阶跃输入信号的响应特性来衡量,如图3-6所示。 这时瞬态响应的性能指标有: 1.最大超调量σ。一响应曲线偏离稳态值的最大值, 常以百分比表示,即 c(p)-c() 最大百分比超调量σ,= ×100% c(o) 最大超调量说明系统的相对稳定性。 2.延滞时间1。一响应曲线到达稳态值50%所需的时间, 称为延滞时间
二、系统的性能指标 系统的瞬态性能通常以系统在初始条件为零的情况下, 对单位阶跃输入信号的响应特性来衡量,如图3-6所示。 这时瞬态响应的性能指标有: 1.最大超调量sp——响应曲线偏离稳态值的最大值, 常以百分比表示,即 最大百分比超调量sp = 最大超调量说明系统的相对稳定性。 2.延滞时间t d——响应曲线到达稳态值50%所需的时间, 称为延滞时间。 % ( ) ( ) ( ) 100 − c c t p c

3.上升时间t一它有几种定义: (1)响应曲线从稳态值的10%到90%所需时间; (2)响应曲线从稳态值的5%到95%所需时间: (3)响应曲线从零开始至第一次到达稳态值所需的时间。 一般对有振荡的系统常用“(3)”,对无振荡的系统常用“(1)”。 4.峰值时间t。一响应曲线到达第一个峰值所需的时间,定义 为峰值时间。 5.调节时间ts—响应曲线从零开始到进入稳态值的 95%~105%(或98%~102%)误差带时所需要的时间,定 义为调节时间
3. 上升时间tr——它有几种定义: (1) 响应曲线从稳态值的10%到90%所需时间; (2) 响应曲线从稳态值的5%到95%所需时间; (3) 响应曲线从零开始至第一次到达稳态值所需的时间。 一般对有振荡的系统常用“(3)”,对无振荡的系统常用“(1)”。 4. 峰值时间tp——响应曲线到达第一个峰值所需的时间,定义 为峰值时间。 5. 调节时间ts——响应曲线从零开始到进入稳态值的 95%~105%(或98%~102%)误差带时所需要的时间,定 义为调节时间

◆c(t) 稳态误差(co) 02 1.00 0.90 ta ±0.02或±0.05 0.50 0.10 安 图3-6单位阶跃响应
图3-6 单位阶跃响应