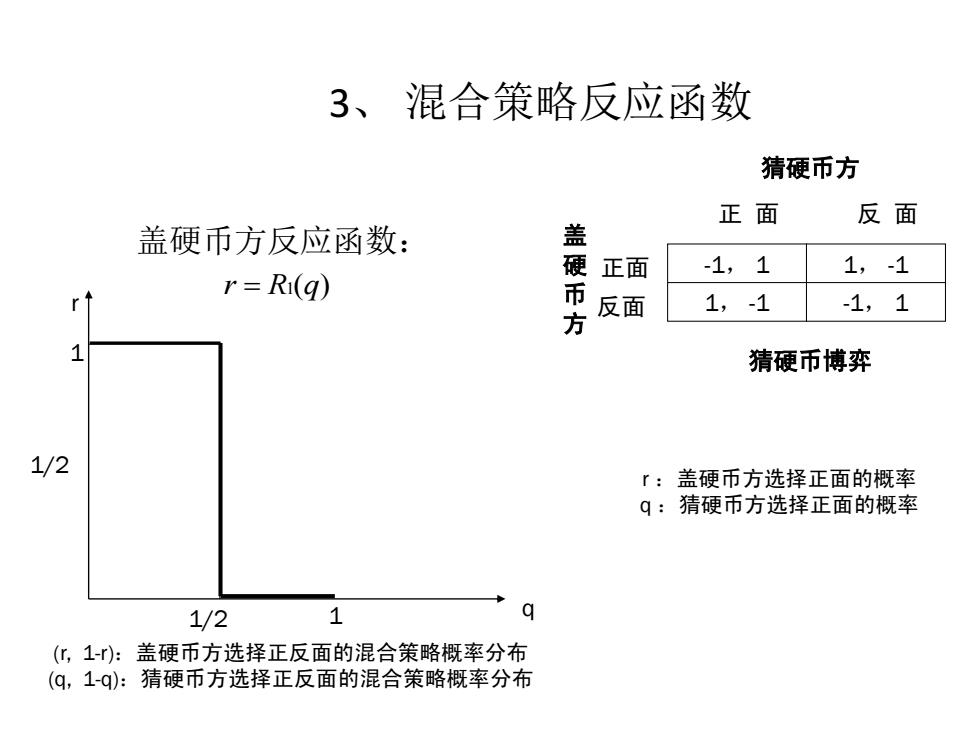
3、混合策略反应函数 猜硬币方 正面 反面 盖硬币方反应函数: 盖 -1,1 1,-1 r Ri(g) 正面 方 反面 1,-1 -1,1 1 猜硬币博弈 1/2 【:盖硬币方选择正面的概率 q:猜硬币方选择正面的概率 1/2 1 q (化1-):盖硬币方选择正反面的混合策略概率分布 (q,1-q):猜硬币方选择正反面的混合策略概率分布
3、 混合策略反应函数 盖硬币方反应函数: -1, 1 1, -1 1, -1 -1, 1 正 面 反 面 猜硬币方 正面 反面 猜硬币博弈 盖 硬 币 方 r q 1 1/2 1 1/2 (r, 1-r):盖硬币方选择正反面的混合策略概率分布 (q, 1-q):猜硬币方选择正反面的混合策略概率分布 r R1(q) r :盖硬币方选择正面的概率 q :猜硬币方选择正面的概率
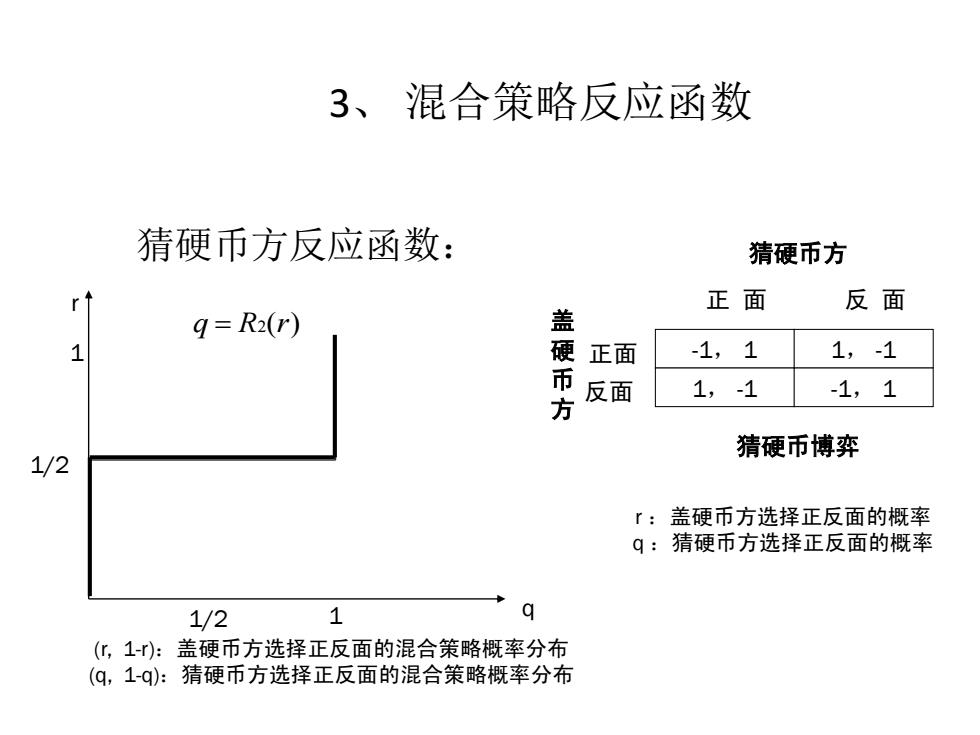
3、混合策略反应函数 猜硬币方反应函数: 猜硬币方 正面 反面 g=R2(r) 1 硬 正面 -1,1 1,-1 方 反面 1,-1 -1,1 猜硬币博弈 1/2 「:盖硬币方选择正反面的概率 q:猜硬币方选择正反面的概率 1/2 1 q (化,1-):盖硬币方选择正反面的混合策略概率分布 (q,1-q):猜硬币方选择正反面的混合策略概率分布
3、 混合策略反应函数 猜硬币方反应函数: -1, 1 1, -1 1, -1 -1, 1 正 面 反 面 猜硬币方 正面 反面 猜硬币博弈 盖 硬 币 方 r q 1 1/2 1 1/2 (r, 1-r):盖硬币方选择正反面的混合策略概率分布 (q, 1-q):猜硬币方选择正反面的混合策略概率分布 q R2(r) r :盖硬币方选择正反面的概率 q :猜硬币方选择正反面的概率
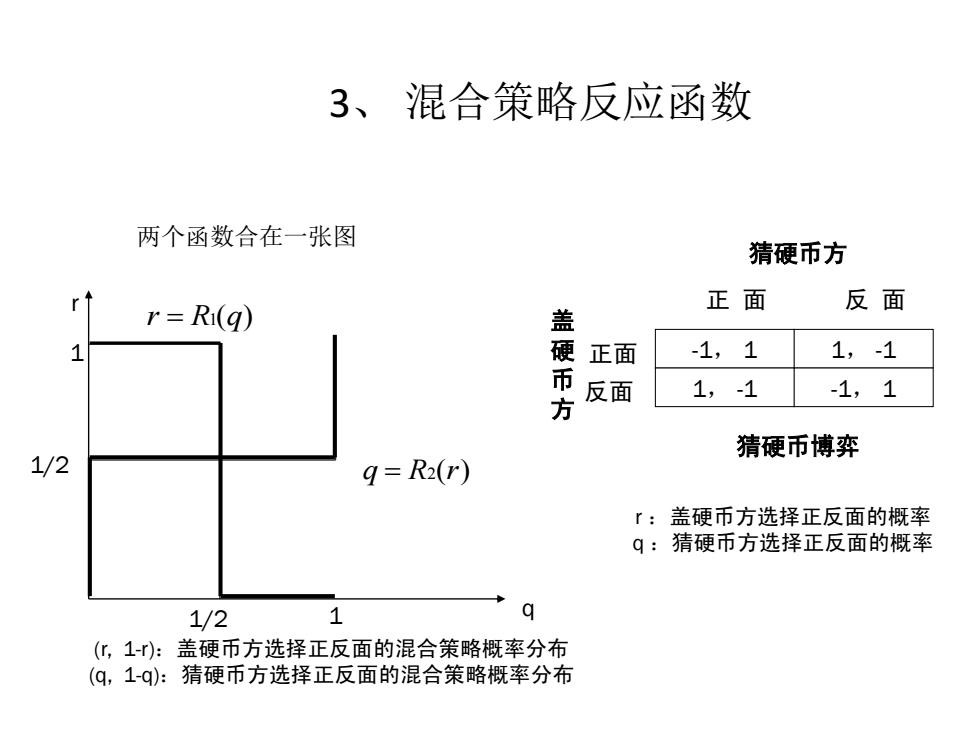
3、混合策略反应函数 两个函数合在一张图 猜硬币方 r=Ri(g) 正面 反面 1 硬 正面 -1,1 1,-1 反面 1,-1 -1,1 方 猜硬币博弈 1/2 q=R2(r) :盖硬币方选择正反面的概率 q:猜硬币方选择正反面的概率 1/2 1 q (化,1-):盖硬币方选择正反面的混合策略概率分布 (q,1-q):猜硬币方选择正反面的混合策略概率分布
3、 混合策略反应函数 两个函数合在一张图 -1, 1 1, -1 1, -1 -1, 1 正 面 反 面 猜硬币方 正面 反面 猜硬币博弈 盖 硬 币 方 r q 1 1/2 1 1/2 (r, 1-r):盖硬币方选择正反面的混合策略概率分布 (q, 1-q):猜硬币方选择正反面的混合策略概率分布 q R2(r) r R1(q) r :盖硬币方选择正反面的概率 q :猜硬币方选择正反面的概率
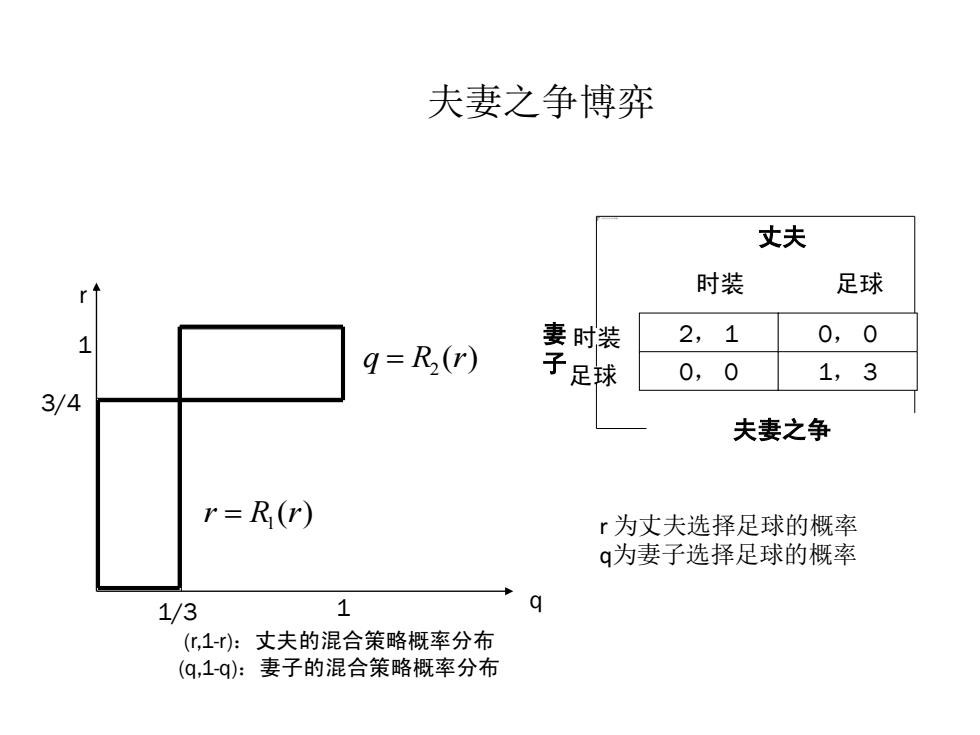
夫妻之争博弈 丈夫 时装 足球 r 1 妻时装 2,1 0,0 q=R(r) 子足球 0,0 1,3 3/4 夫妻之争 r=R(r) 为丈夫选择足球的概率 q为妻子选择足球的概率 1/3 1 (,1-):丈夫的混合策略概率分布 (q,1-q):妻子的混合策略概率分布
夫妻之争博弈 2, 1 0, 0 0, 0 1, 3 时装 足球 丈夫 时装 足球 妻 子 夫妻之争 r q 1 1/3 1 3/4 (r,1-r):丈夫的混合策略概率分布 (q,1-q):妻子的混合策略概率分布 ( ) 2 q R r ( ) 1 r R r r 为丈夫选择足球的概率 q为妻子选择足球的概率

4、纳什均衡的存在性 纳什定理:在一个由n个博弈方的博弈G={S,…Sn,4,un}中, 如果n是有限的,且S都是有限集时(i=1,n),则该博弈至 少存在一个纳什均衡,但可能包含混合策略。 ·主要根据是布鲁威尔和角谷的不动点定理。 ·纳什均衡的普遍存在性正是纳什均衡成为非合作博弈分析核 心概念的根本原因之一
4、 纳什均衡的存在性 纳什定理:在一个由n个博弈方的博弈 中, 如果n是有限的,且 都是有限集时( ),则该博弈至 少存在一个纳什均衡,但可能包含混合策略。 • 主要根据是布鲁威尔和角谷的不动点定理。 • 纳什均衡的普遍存在性正是纳什均衡成为非合作博弈分析核 心概念的根本原因之一。 { , ; , } G S1 Sn u1 un i S i 1, n

5、纳什均衡的选择和分析方法扩展 一、多重纳什均衡博弈的分析 二、共谋和防共谋均衡
5、 纳什均衡的选择和分析方法扩展 一、多重纳什均衡博弈的分析 二、共谋和防共谋均衡

一、多重纳什均衡博弈的分析 ·帕累托上策均衡 ·风险上策均衡 ·聚点均衡 。相关均衡
一、 多重纳什均衡博弈的分析 • 帕累托上策均衡 • 风险上策均衡 • 聚点均衡 • 相关均衡
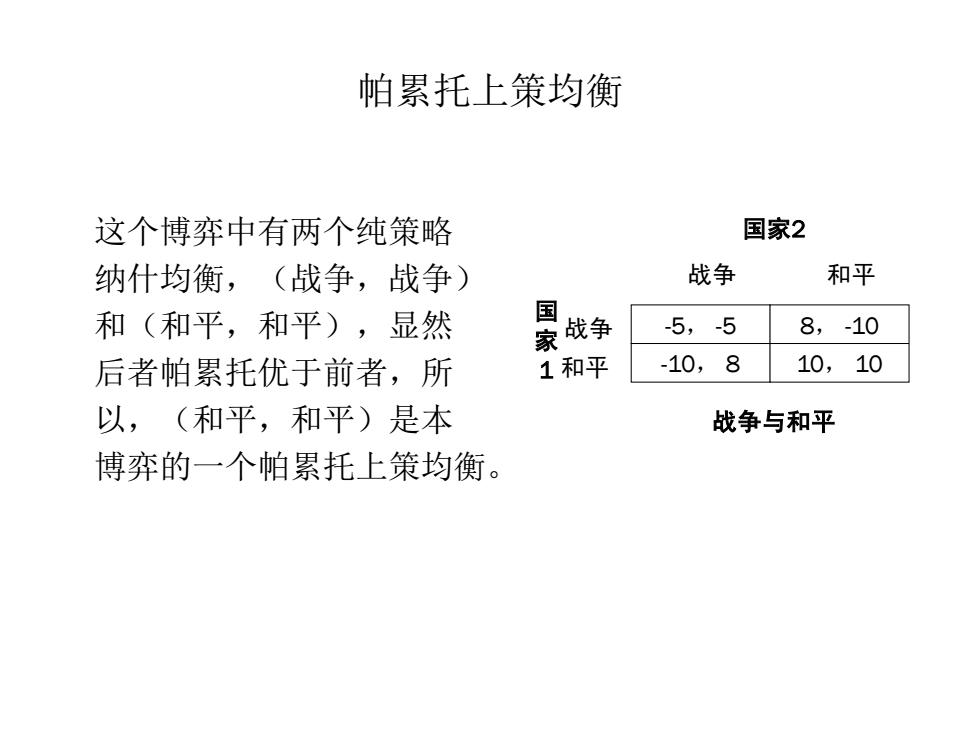
帕累托上策均衡 这个博弈中有两个纯策略 国家2 纳什均衡,(战争,战争) 战争 和平 和(和平,和平),显然 景极争 5,-5 8,-10 后者帕累托优于前者,所 1和平 -10,8 10,10 以,(和平,和平)是本 战争与和平 博弈的一个帕累托上策均衡
帕累托上策均衡 这个博弈中有两个纯策略 纳什均衡,(战争,战争) 和(和平,和平),显然 后者帕累托优于前者,所 以,(和平,和平)是本 博弈的一个帕累托上策均衡。 -5, -5 -10, 8 8, -10 10, 10 战争 和平 国家2 战争 和平 国 家 1 战争与和平
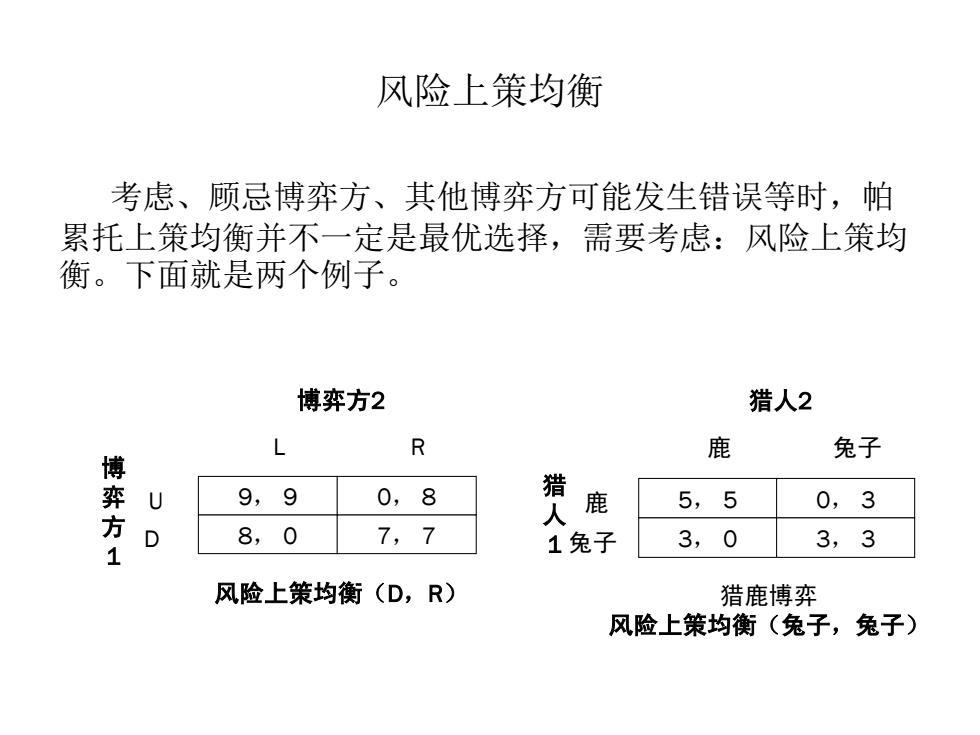
风险上策均衡 考虑、顾忌博弈方、其他博弈方可能发生错误等时,帕 累托上策均衡并不一定是最优选择,需要考虑:风险上策均 衡。下面就是两个例子。 博弈方2 猎人2 L R 鹿 兔子 博 方 U 9,9 0,8 人 鹿 5,5 0,3 1 D 8,0 7,7 兔子 3,0 3,3 风险上策均衡(D,R) 猎鹿博弈 风险上策均衡(兔子,兔子)
风险上策均衡 考虑、顾忌博弈方、其他博弈方可能发生错误等时,帕 累托上策均衡并不一定是最优选择,需要考虑:风险上策均 衡。下面就是两个例子。 9, 9 8, 0 0, 8 7, 7 L R 博弈方2 U D 博 弈 方 1 风险上策均衡(D,R) 5, 5 3, 0 0, 3 3, 3 鹿 兔子 猎人2 鹿 兔子 猎 人 1 猎鹿博弈 风险上策均衡(兔子,兔子)
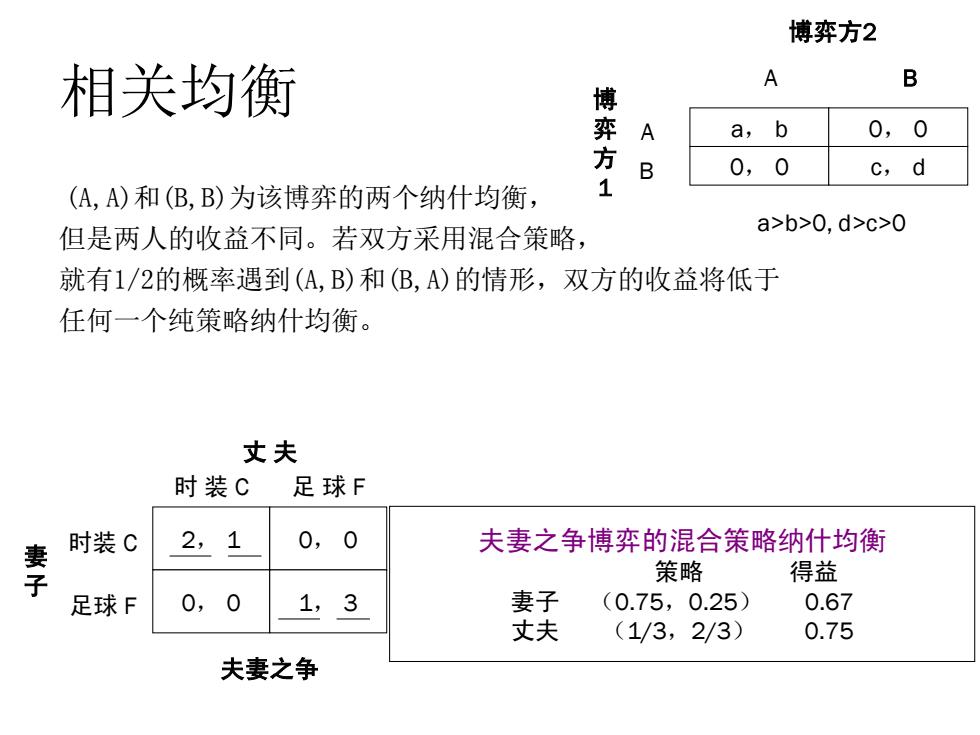
博弈方2 相关均衡 A B 博 A a,b 0,0 方 B 0,0 C, a (A,A)和(B,B)为该博弈的两个纳什均衡, 1 但是两人的收益不同。若双方采用混合策略, a>b>0,d>c>0 就有1/2的概率遇到(A,B)和(B,A)的情形,双方的收益将低于 任何一个纯策略纳什均衡。 丈夫 时装C 足球F 0,0 妻 时装C 2,1 夫妻之争博弈的混合策略纳什均衡 策略 得益 足球F 0,0 1,3 妻子 (0.75,0.25) 0.67 丈夫 (1/3,2/3) 0.75 夫妻之争
相关均衡 (A,A)和(B,B)为该博弈的两个纳什均衡, 但是两人的收益不同。若双方采用混合策略, 就有1/2的概率遇到(A,B)和(B,A)的情形,双方的收益将低于 任何一个纯策略纳什均衡。 a, b 0, 0 0, 0 c, d A B 博弈方2 A B 博 弈 方 1 a>b>0, d>c>0 2, 1 0, 0 0, 0 1, 3 时 装 C 足 球 F 时装 C 足球 F 丈 夫 妻 子 夫妻之争 夫妻之争博弈的混合策略纳什均衡 策略 得益 妻子 (0.75,0.25) 0.67 丈夫 (1/3,2/3) 0.75