《线性代数》课程教学课件（讲稿，B）第一章 第一节

线性代数的主要内容 解的存在性 线性方程组求解 解的结构 一次方程 行列式 由高斯消元法引入两个求解工具 矩阵 一个中心方法：矩阵的初等行变换 一个应用：二次曲线和二次曲面的形状判定 加油！

一个应用：二次曲线和二次曲面的形状判定 线性方程组求解    解的存在性 解的结构 由高斯消元法引入两个求解工具    行列式 矩阵 一个中心方法：矩阵的初等行变换 一次方程 线性代数的主要内容

41x1+412X2=b1, () 421X1+422X2=b2 (2) 用高斯消元法求其解： 442七1+☑42zr2=b,42←-(0×42 -）421412大1+224x2=b2412(2)×42 (422-412421）X1=b42-42b2 加油！

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 22 (1)  a 12 ) (2)  a 11 22 12 21 1 1 22 12 2 （a a a a x b a a b    ） 用高斯消元法求其解： 21 12 1 22 12 2 2 12 a a x a a x b a   11 22 1 12 22 2 1 22 a a x a a x b a  

411k1+412X2=b1, () 21X1+422X2=b2· (2) a241比1+42241X2=b2411←-(2)×4 442X1+412421X2=b,421(①×4！ (41n42-412421）X2=41b2-b421 加油！

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 11 22 12 21 2 11 2 1 21 （a a a a x a b b a    ） 21 11 1 22 11 2 2 11 a a x a a x b a   11 (2)  a 21 ) (1)  a 11 21 1 12 21 2 1 21 a a x a a x b a  

二阶行列式定义 由四个数排成二行二列（横排称行、竖排称列） 的数表 011012 L21022 (4) 数411422-4122 称为数表(4)所确定的 二阶行列式，记为 411412 L21 22 加油！

由四个数排成二行二列（横排称行、竖排称列） 的数表 (4) 21 22 11 12 a a a a 数 a a a a 11 22 12 21  称为数表（4）所确定的 二阶行列式, 记为 11 12 21 22 a a a a 二阶行列式定义

例1求解二元线性方程组 3x1-2x2=12, 2x1+x2=1 解D-X=3-()=7≠机 ”=X7=44-X=-2 .X1= D-1 4=2,= D=-21 D 3. 加油！

例 1      2 1 . 3 2 12 , 1 2 1 2 x x x x 解 2 1 3  2 D   3  (  4 )  7  0 , 1 1 12 2 1  D   14 , 2 1 3 12 D 2   21 , DD x 1  1  2 , 7 14   DD x 2 2  3. 7 21     求解二元线性方程组

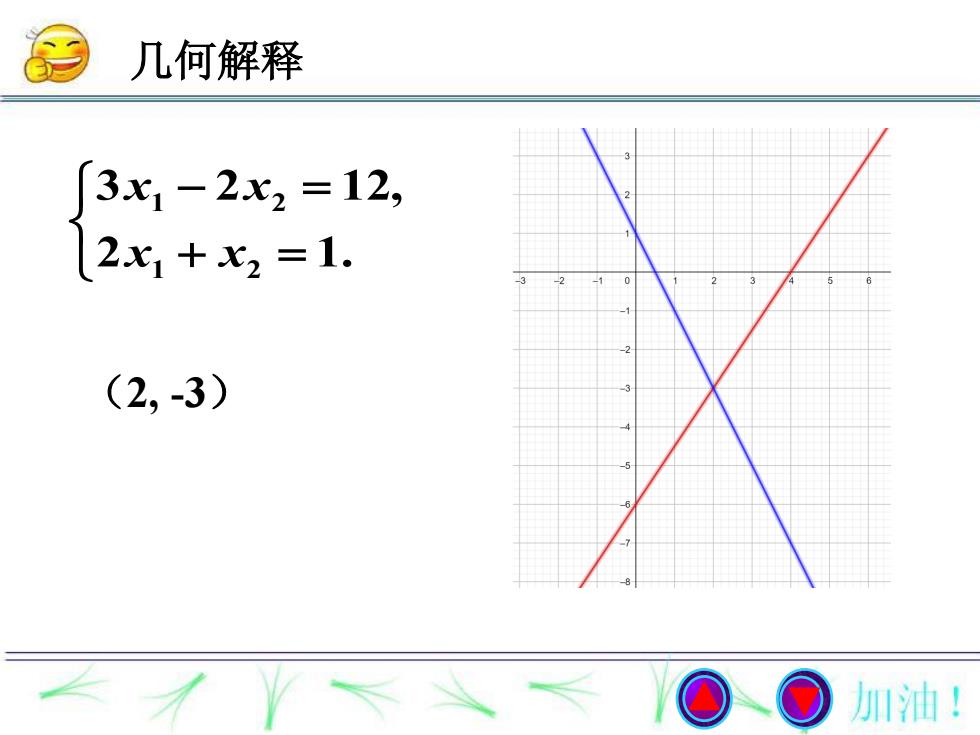
几何解释 3x1-2x2=12, 2x1+x2=1. (2,3) 加油！

       2 1. 3 2 12, 1 2 1 2 x x x x （2, -3） 几何解释

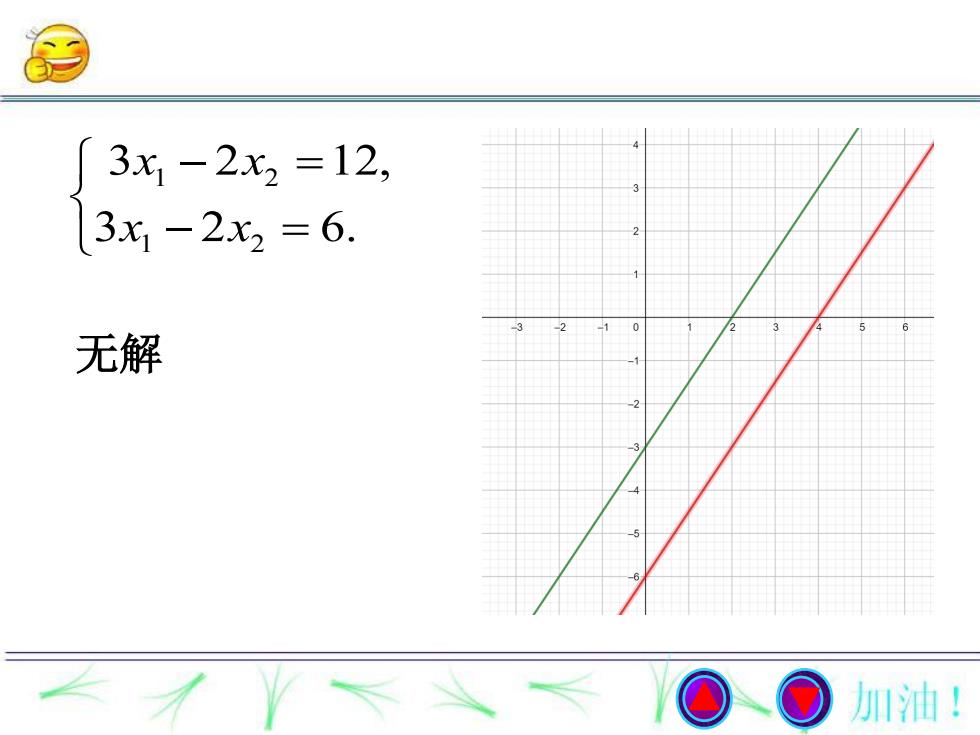
3x1-2x2=12, 3x1-2x2=6. 无解 加油！

1 2 1 2 3 2 12, 3 2 6. x x x x        无解

3x1-2x2=12, 6x1-4x2=24. 无穷多的解 加油！

1 2 1 2 3 2 12, 6 4 24. x x x x        无穷多的解

三阶行列式的引出 411X1+412X2+413X3=b1 21K1+022x2+23X3=b2 031x1+432X2+M33X3=b3 加油！

三阶行列式的引出               31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b

41X1+412x2+13X3=b1 1 C12 3 421x1+a22K2+L23X3=b2 D a21 022 023 431X1+a32X2+a33X3=b3 a31 32 033 当D≠0时，三元线性方程组的解为： D D: X1= D ，2= D X3= D b a11 b a13 a11a42 b a12 a13 D3= a21 D= b2 a22 a23 D2= a1 b2 d23 an b b a a32 a33 a31 b a33 加油！

1 2 3 1 2 3 0 , , D D D D x x x D D D     当 时，三元线性方程组的解为： 11 12 13 21 22 23 31 32 33 a a a D a a a a a a  1 12 13 1 2 22 23 3 32 33 b a a D b a a b a a                31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b 11 1 13 2 21 2 23 31 3 33 a b a D a b a a b a  11 12 1 3 21 22 2 31 32 3 a a b D a a b a a b 