
第二节行列式的性质与计算 目的要求: 掌握行列式的性质 熟练运用行列式的性质 化行列式为三角行列式 加油!
第二节 行列式的性质与计算 目的要求: 掌握行列式的性质 熟练运用行列式的性质 化行列式为三角行列式

一、n阶行列式的定义的推广 定理1 阶行列式等于它的任意一行(列)的各个元素 与其对应的代数余子式的乘积之和,即有 D=01Ai+.+4A+.+0mAmi=1,2,.,n 或者 D=a1yA+.+aA++mAgj=1,2,.,n 加油!
D ai1 Ai1 aijAij ainAin i 1,2, ,n 或者 D a1 j A1 j aijAij anjAnj j 1,2, ,n 一、 n阶行列式的定义的推广 定理1 n阶行列式等于它的任意一行(列)的各个元素 与其对应的代数余子式的乘积之和,即有

© 二、行列式的性质 加油!
二、行列式的性质
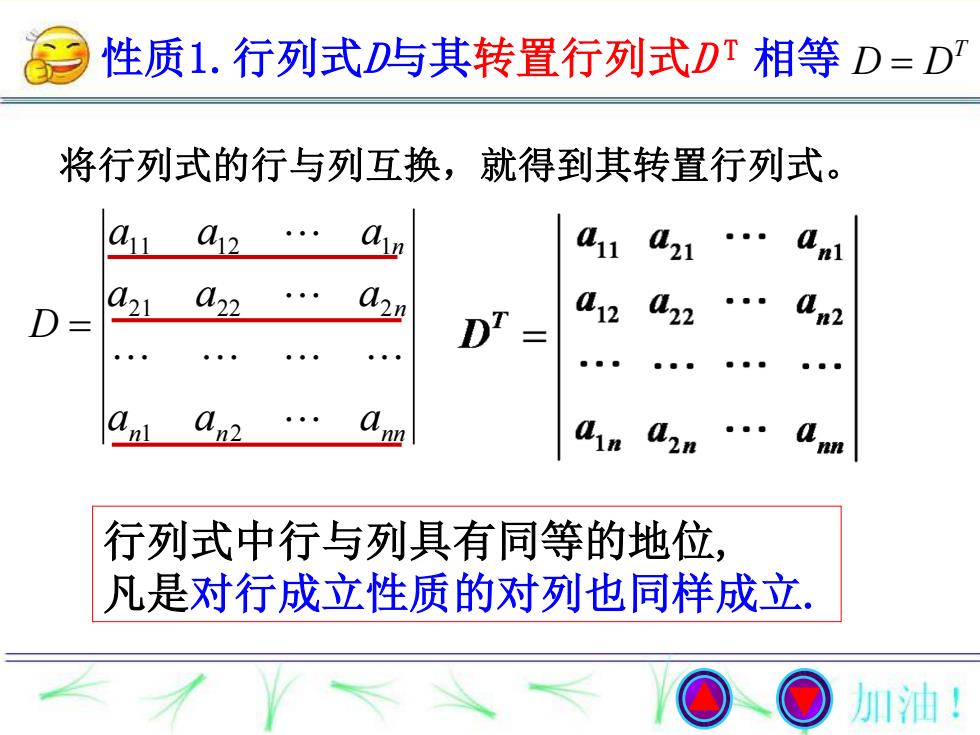
性质1.行列式D与其转置行列式Dr相等D=D 将行列式的行与列互换,就得到其转置行列式。 12 411 421 22 D 02y DT a2 22 02 。 nl n2 0必 41n 行列式中行与列具有同等的地位, 凡是对行成立性质的对列也同样成立. 加油!
性质1.行列式D与其转置行列式D T 相等 n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 将行列式的行与列互换,就得到其转置行列式。 行列式中行与列具有同等的地位, 凡是对行成立性质的对列也同样成立. T D D
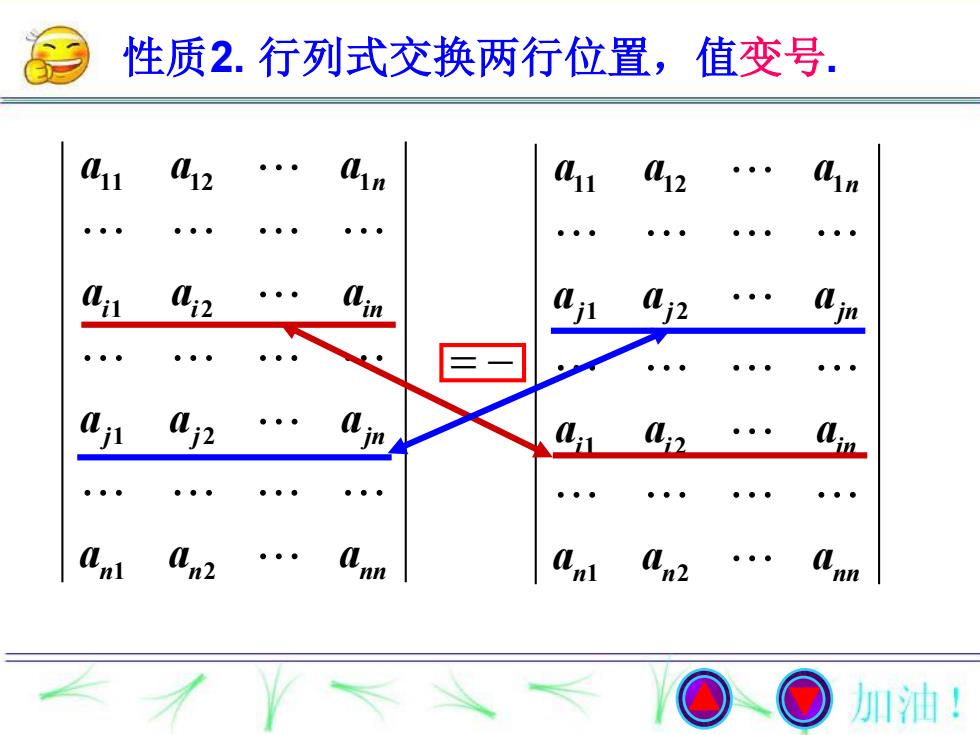
性质2.行列式交换两行位置,值变号. 1 12 31 12 a;2 02 ●●● 01 0j2 0: w ●●● ●●● ●● ●章● ●●● ●●● ●●● 。●● nn 2 W 加油!
性质2. 行列式交换两行位置,值变号. 11 12 1 1 2 1 2 1 2 n i i in j j jn n n nn a a a a a a a a a a a a 11 12 1 1 2 1 2 1 2 n j j jn i i in n n nn a a a a a a a a a a a a

推论.行列式中有两行元素对应相等, 行列式的值为零. 加油!
推论 .行列式中有两行元素对应相等, 行列式的值为零

性质3.行列式某一行的所有元素都乘 以同 一数k,等于用数k乘以此行列式。 1 12 1 C12 n 。 ●●● ka ka;2 。 02 。· 。 an 0n2 ann an2 加油!
性质3. 行列式某一行的所有元素都乘 以同一数k,等于用数k乘以此行列式。 n n nn i i i n n a a a ka ka ka a a a 1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a 1 2 1 2 11 12 1 k

推论.行列式中某一行的元素的公因子可 以提到行列式的外面. 推论.行列式中某一行的元素全为零,则 行列式为零. 推论.行列式中两行元素对应成比例,则 行列式为零. 油!
推论. 行列式中某一行的元素的公因子可 以提到行列式的外面. 推论. 行列式中两行元素对应成比例,则 行列式为零. 推论. 行列式中某一行的元素全为零,则 行列式为零
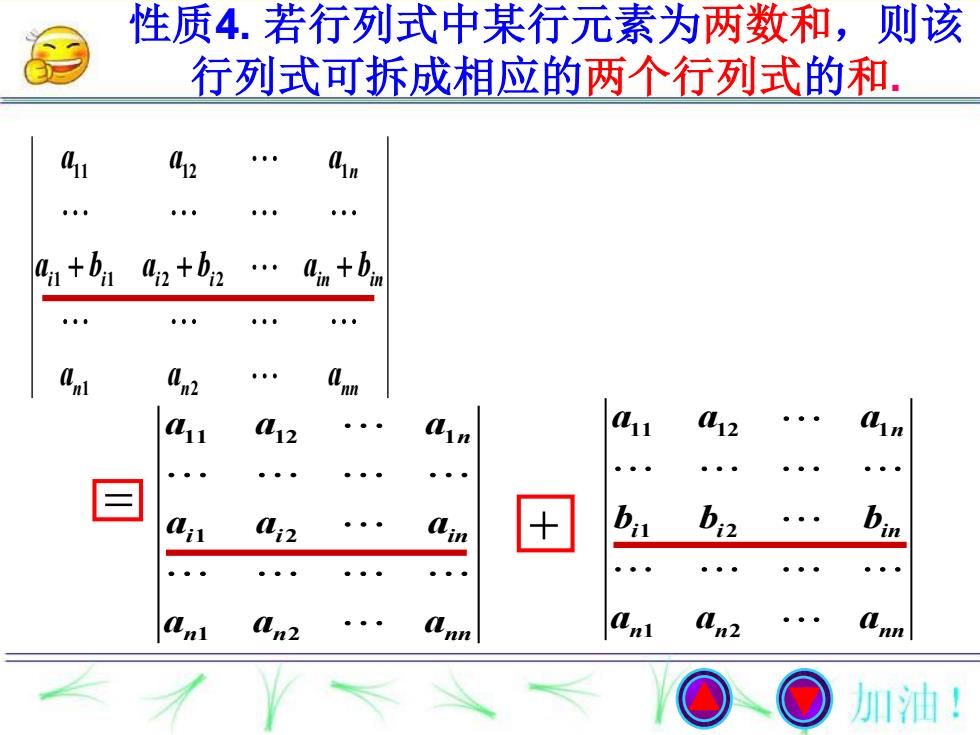
性质4.若行列式中某行元素为两数和,则该 行列式可拆成相应的两个行列式的和. 411 1+b 42+b2 ain +bin 1 L12 n 31 a2 ●●● 。 。●● ●●● ai2 b an2 l2 加油!
性质4. 若行列式中某行元素为两数和,则该 行列式可拆成相应的两个行列式的和. 11 12 1 1 1 2 2 1 2 n i i i i in in n n nn a a a a b a b a b a a a 11 12 1 1 2 1 2 n i i in n n nn a a a a a a a a a 11 12 1 1 2 1 2 n i i in n n nn a a a b b b a a a
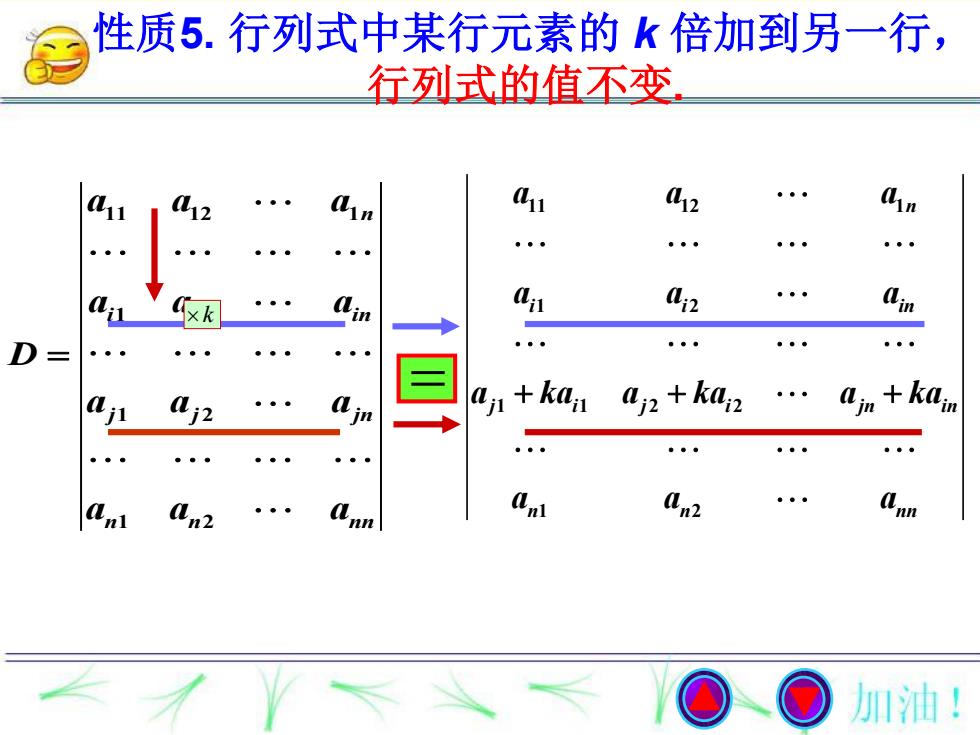
性质5.行列式中某行元素的k倍加到另一行, 行列式的值不变 1 2 n in w 2 Qin D 。 。 aj a;z aj2+ka2. ajn +kain in . 2 加油!
性质5. 行列式中某行元素的 k 倍加到另一行, 行列式的值不变. 11 12 1 1 2 1 1 2 2 1 2 n i i in j i j i jn in n n nn a a a a a a a ka a ka a ka a a a 11 12 1 1 2 1 2 1 2 n i i in j j jn n n nn a a a a a a D a a a a a a k