
§13-1热辐射普朗克的能量子假设 一、热辐射现象 固体或液体,在任何温度下都在发射各种波长 的电磁波,这种由于物体中的分子、原子受到激发 而发射电磁波的现象称为热辐射。所辐射电磁波的 特征仅与温度有关。 固体在温度升高时颜色的变化 800K 1000K 1200K 1400K 物体辐射总能量及能量按波长分布都决定于温度。 美子京道回退
上页 下页 返回 退出 固体或液体,在任何温度下都在发射各种波长 的电磁波,这种由于物体中的分子、原子受到激发 而发射电磁波的现象称为热辐射。所辐射电磁波的 特征仅与温度有关。 固体在温度升高时颜色的变化 1400K 物体辐射总能量及能量按波长分布都决定于温度。 800K 1000K 1200K §13-1 热辐射 普朗克的能量子假设 一、热辐射现象

二、基尔霍夫辐射定律 1.单色辐出度:单位时间内,温度为T的物体单 位面积上发射的波长在倒入范勇内的辐射能量 与波间隔的比值, 表示M(T) M,(T)= dE dλ 单色辐出度M,(T与物体的温度和辐射波长有关。 2.辐出度:单位时间内,从物体单位面积上所 发射的各种波长的总辐射能,称为物体的辐射出 射度,简称辐出度。 让美下觉返同速
上页 下页 返回 退出 单色辐出度 M T ( ) 与物体的温度和辐射波长有关。 d ( ) d E M T = 1.单色辐出度:单位时间内,温度为T 的物体单 位面积上发射的波长在 到 范围内的辐射能量 与波长间隔 的比值,用 表示 + d dE d M T( ) 二、基尔霍夫辐射定律 2.辐出度: 单位时间内,从物体单位面积上所 发射的各种波长的总辐射能,称为物体的辐射出 射度,简称辐出度

M(T)=6M(T)d入 辐出度只是物体温度的函数。 3.单色吸收比和单色反射比:被物体吸收的能量与 入射能量之比称为吸收比。在波长到入+随围内 的吸收比称为单色吸收比,用α2(砖示;反射的能量 与入射能量之比称为反射比,波长到九+苑围内的 反射比称为单色反射比,用r(砖示。 绝对黑体:若物体在任何温度下,对任何波长的 辐射能的吸收比都等于1,则称该物体为绝对黑体,简 称黑体
上页 下页 返回 退出 = 0 M (T) M (T)d 辐出度只是物体温度的函数。 3.单色吸收比和单色反射比: 被物体吸收的能量与 入射能量之比称为吸收比。在波长 到 范围内 的吸收比称为单色吸收比,用 表示;反射的能量 与入射能量之比称为反射比,波长 到 范围内的 反射比称为单色反射比,用 表示。 + d a (T) + d r (T) 绝对黑体: 若物体在任何温度下,对任何波长的 辐射能的吸收比都等于1,则称该物体为绝对黑体,简 称黑体

基尔霍夫辐射定律:在同样的温度下,各种不同物体 对相同波长的单色辐出度与单色吸收比之比值都相 等,并等于该温度下黑体对同一波长的单色辐出度。 Ma(T)_M22(T) a1(T) a2(T) =.=M0(T) 即好的吸收体也是好的辐射体。 三、黑体辐射实验定律 不透明的材料制成带小孔的空腔,可近似看作黑 体。 研究黑体辐射的规律是 了解一般物体热辐射性质的 黑体模型 基础。 让美子觉返同速
上页 下页 返回 退出 基尔霍夫辐射定律: 在同样的温度下,各种不同物体 对相同波长的单色辐出度与单色吸收比之比值都相 等,并等于该温度下黑体对同一波长的单色辐出度。 ( ) ( ) ( ) ( ) ( ) 0 2 2 1 1 M T a T M T a T M T = == 即好的吸收体也是好的辐射体。 不透明的材料制成带小孔的空腔,可近似看作黑 体。 黑 体 模 型 研究黑体辐射的规律是 了解一般物体热辐射性质的 基础。 三、黑体辐射实验定律

黑体辐射 让意不家返可退此
上页 下页 返回 退出 黑体辐射
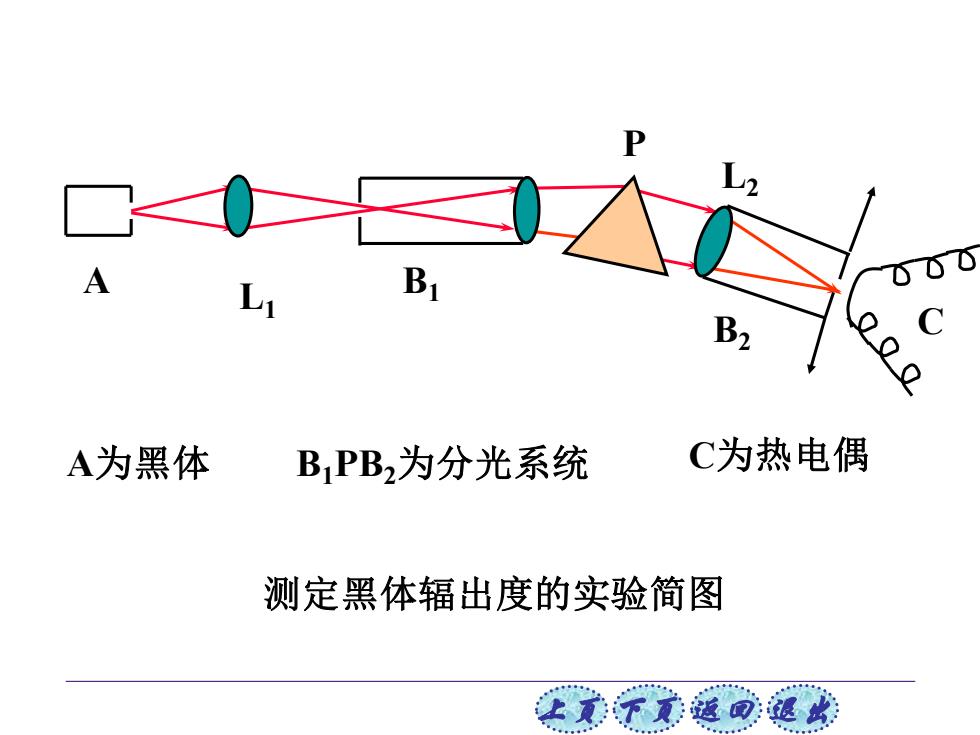
A B A为黑体 BPB2为分光系统 C为热电偶 测定黑体辐出度的实验简图 让美下觉返司速此
上页 下页 返回 退出 测定黑体辐出度的实验简图 P L2 B2 A L1 B1 C A为黑体 B1PB2为分光系统 C为热电偶
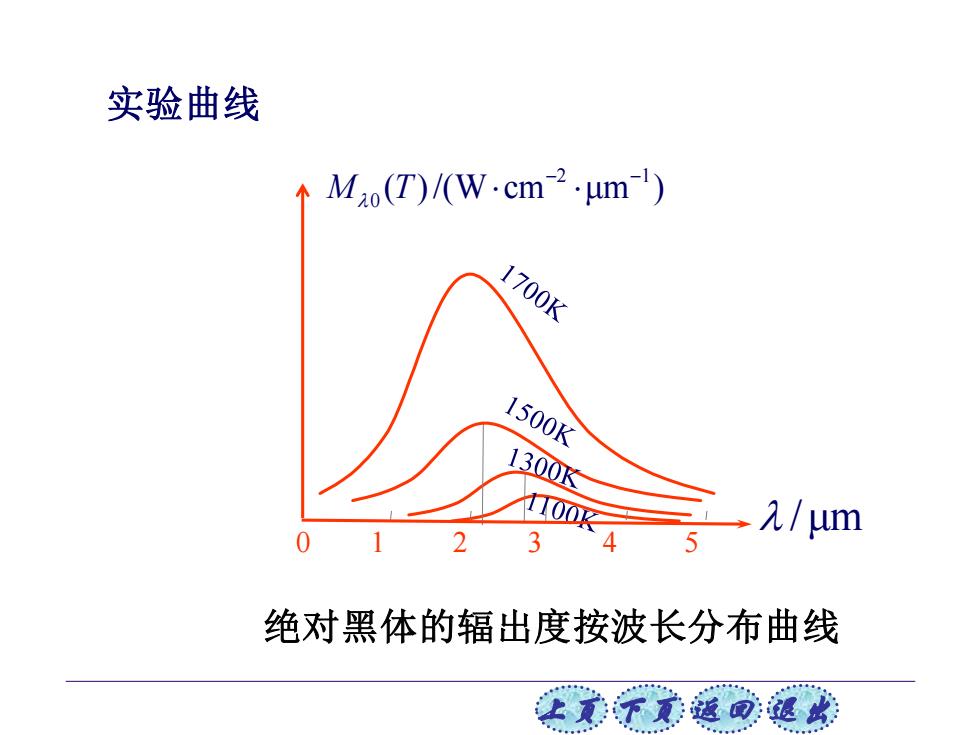
实验曲线 ↑Mo(T)/(W.cm-2·μm) 1700K 1500K 1300K 100 元/μm 2 3 5 绝对黑体的辐出度按波长分布曲线 让贰下觉返回退
上页 下页 返回 退出 0 1 2 3 4 5 2 1 0 M T( ) /(W cm μm ) − − / μm 绝对黑体的辐出度按波长分布曲线 实验曲线

根据实验得出黑体辐射的两条定律: 1.斯特藩-玻耳兹曼定律 黑体的辐出度与黑体的绝对温度四次方成正比 Mo(T)=oT 斯特藩常数 o=5.67×10-8W/(m2.K4) 热辐射的功率随着温度的升高而迅速增加。 2.维恩位移定律 对于给定温度T,黑体的单色辐出度 有0 最大值,其对应波长为入m Th=b 维恩常量b=2.897×103mK 热辐射的峰值波长随着温度的增加而向着短波方向移动。 江觉子觉道司退此
上页 下页 返回 退出 4 0 M T T ( ) = 黑体的辐出度与黑体的绝对温度四次方成正比 1. 斯特藩-玻耳兹曼定律 根据实验得出黑体辐射的两条定律: 热辐射的功率随着温度的升高而迅速增加。 斯特藩常数 5.67 10 W/(m K ) 8 2 4 = − T b m = 热辐射的峰值波长随着温度的增加而向着短波方向移动。 2. 维恩位移定律 维恩常量 b=2.897×10-3m·K 对于给定温度T ,黑体的单色辐出度 有一 最大值,其对应波长为 。 M0 m

例题13-1实验测得太阳辐射波谱的2.=490nm, 若把太阳视为黑体,试计算(1)太阳每单位表面积上 所发射的功率;(2)地球表面阳光直射的单位面积上 接受到的辐射功率;(3)地球每秒内接受的太阳辐射 能(已知太阳半Rs=6.96×108m,地球半径 Rp=6.37×106m,地球到太阳的距离d=1.496×101山m) 解:(1)根据维恩位移定律2T=b 7、6 =5.9×103K 根据斯特藩-玻尔兹曼定律可求出辐出度,即单位 表面积上的发射功率 M=oT4=6.87×107W/m2 让无子文返回退此
上页 下页 返回 退出 3 5.9 10 b T = = m K 解 :(1)根据维恩位移定律 m T b = 根据斯特藩-玻尔兹曼定律可求出辐出度,即单位 表面积上的发射功率 例题13-1 实验测得太阳辐射波谱的 , 若把太阳视为黑体,试计算(1)太阳每单位表面积上 所发射的功率;(2)地球表面阳光直射的单位面积上 接受到的辐射功率;(3)地球每秒内接受的太阳辐射 能(已知太阳半RS=6.96×108m,地球半径 RE=6.37×106m,地球到太阳的距离d=1.496×1011m) m = 490nm 4 7 2 0 M T = = 6.87 10 / W m

(2)太阳辐射的总功率 P=M4rR=4.2×1026W 这功率分布在以太阳为中心、以日地距离为 半径的球面上,故地球表面单位面积接受到的辐 射功率 P P:= =1.49×103W/m2 4πd2 (3)由于地球到太阳的距离远大于地球半径, 可将地球看成半径为R的圆盘,故地球接受到太 阳的辐射能功率 =P×TR2=1.90×107W 王觉下元菠面:退收
上页 下页 返回 退出 (2)太阳辐射的总功率 这功率分布在以太阳为中心、以日地距离为 半径的球面上,故地球表面单位面积接受到的辐 射功率 2 26 0 P M R = = 4 4.2 10 S S π W 3 2 1.49 10 4 P P d = = S 2 E W/m π (3)由于地球到太阳的距离远大于地球半径, 可将地球看成半径为RE的圆盘,故地球接受到太 阳的辐射能功率 2 17 P P R = = 1.90 10 E E E π W