
§13-10电子的自旋原子的电子壳层结构 一、施特恩-格拉赫实验 N 1921年,施特恩(O.Stern)和格拉赫( W.Gerlach)发现一些处于S态的原子射线 束,在非均匀磁场中一束分为两束。 让美觉返司退
上页 下页 返回 退出 1921年,施特恩(O.Stern)和格拉赫( W.Gerlach)发现一些处于S态的原子射线 束,在非均匀磁场中一束分为两束。 一、施特恩-格拉赫实验 §13-10 电子的自旋 原子的电子壳层结构

二、电子的自旋 1925年,鸟伦贝克(G.E.Uhlenbeck) 和古兹密特(S.A.Goudsmit)提出电子自旋假说。把 电子绕自身轴线的转动称为自旋。 由自旋产生的磁矩称 为自旋磁矩4、,由自旋 产生的角动量为S,其方 向与磁矩方向相反。 电子的自旋 让意子美返同退此
上页 下页 返回 退出 由自旋产生的磁矩称 为自旋磁矩 ,由自旋 产生的角动量为 ,其方 向与磁矩方向相反。 s S 1925年,乌伦贝克 ( G.E.Uhlenbeck ) 和古兹密特(S.A.Goudsmit)提出电子自旋假说。把 电子绕自身轴线的转动称为自旋。 电子的自旋 二、电子的自旋
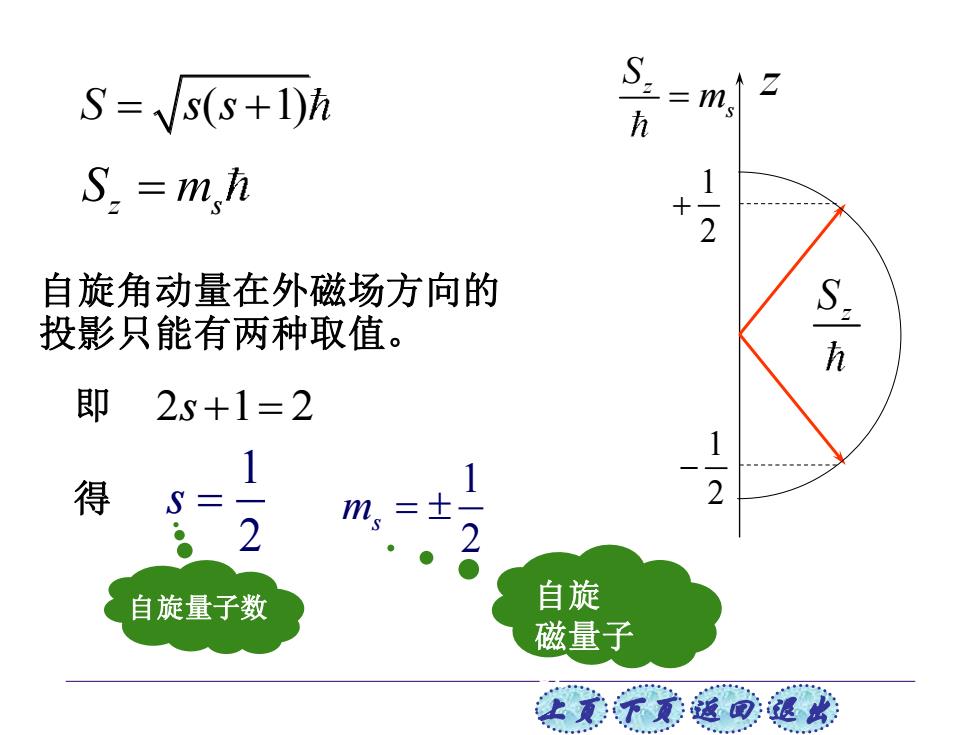
S=√s(s+1)h S.=mh 自旋角动量在外磁场方向的 S. 投影只能有两种取值。 即 2s+1=2 1 得 S 2 ms 2 自旋量子数 自旋 磁量子 在美不觉返同速
上页 下页 返回 退出 自旋 磁量子 数 自旋角动量在外磁场方向的 投影只能有两种取值。 即 得 1 2 s = 1 2 ms = 自旋量子数 S s s = + ( 1) z s S m= 2 1 2 s + = z z s S = m z S 1 2 + 1 2 −

三、原子的壳层结构 原子中电子的状态由四个量子数确定 1.主量子数n=1,2,3,.大体上决定电子在原子中的能量 2.角量子数1=0,1,2,.,(n-1) 决定电子绕核运动的角动量 L=Vl(1+1)h 3.磁量子数m=0,士1,+2,.,±1 决定电子绕核运动角动量的空间取向 4.自旋磁量子数m,=士 2 决定电子自旋角动量的空间取向 让意了意适回退块
上页 下页 返回 退出 原子中电子的状态由四个量子数确定 1.主量子数 n=1,2,3,. 大体上决定电子在原子中的能量 2.角量子数 l =0, 1, 2, ., (n-1) 决定电子绕核运动的角动量 L = l(l+1) 决定电子绕核运动角动量的空间取向 3.磁量子数 0, 1, 2, , m l l = 4.自旋磁量子数 2 1 ms = 决定电子自旋角动量的空间取向 三、原子的壳层结构

一般地,主量子数n越大的主壳层其能级越高; 在同一主壳层内,副量子数1越大的支壳层其能 级越高。但也有例外,实际上能级的高低次序 可表示为 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 6d. 让美下觉返司速此
上页 下页 返回 退出 一般地,主量子数n越大的主壳层其能级越高; 在同一主壳层内,副量子数l越大的支壳层其能 级越高。但也有例外,实际上能级的高低次序 可表示为 1s 5d 7s 5s 5p 6s 6p 6d . 4s 3s 3p 4f 3d 4p 4d 2s 2p

电子在原子中的分布遵从下列两个原理: 1.泡利不相容原理 泡利在1925年提出:在原子中,不可能有两个或 两个以上的电子具有完全相同的量子态。也就是说, 原子中任何两个电子的量子数(n,1,m,m,不可能完全 相同。这个结论叫泡利不相容原理。 让美不家返可退此
上页 下页 返回 退出 1.泡利不相容原理 电子在原子中的分布遵从下列两个原理: 泡利在1925年提出:在原子中,不可能有两个或 两个以上的电子具有完全相同的量子态。也就是说, 原子中任何两个电子的量子数 不可能完全 相同。这个结论叫泡利不相容原理。 ( , , , ) l s n l m m

据泡利不相容原理,对于某一支壳层,对 应的量子数为n和l,即处于该支壳层的电子具 有相同的能量和角动量数值,但其磁量子数可 取m=0,1,2,.,士,共2+1种可能值,对每一 个m值又有两种m,值。因此,在同一支壳层上 可容纳的电子数为 W,=2(21+1) 对于某一主壳层n,其副量子数可取0,1,2,., -1种可能值,而对每一1值,可容纳电子数为 2(2+1)种,故在主壳层n上可容纳的电子数为 n-1 Nn=∑2(21+1)=2n2 n=0 让美下元返回退欢
上页 下页 返回 退出 据泡利不相容原理,对于某一支壳层,对 应的量子数为 n和 l, 即处于该支壳层的电子具 有相同的能量和角动量数值, 但其磁量子数可 取 , 共2l+1种可能值,对每一 个ml值又有两种ms值。因此,在同一支壳层上 可容纳的电子数为 0, 1, 2, , l m l = 对于某一主壳层n,其副量子数可取 0, 1, 2, ., n-1种可能值,而对每一 l 值,可容纳电子数为 2(2l+1)种,故在主壳层n上可容纳的电子数为 2(2 1) N l l = + 1 2 0 2(2 1) 2 n n n N l n − = = + =
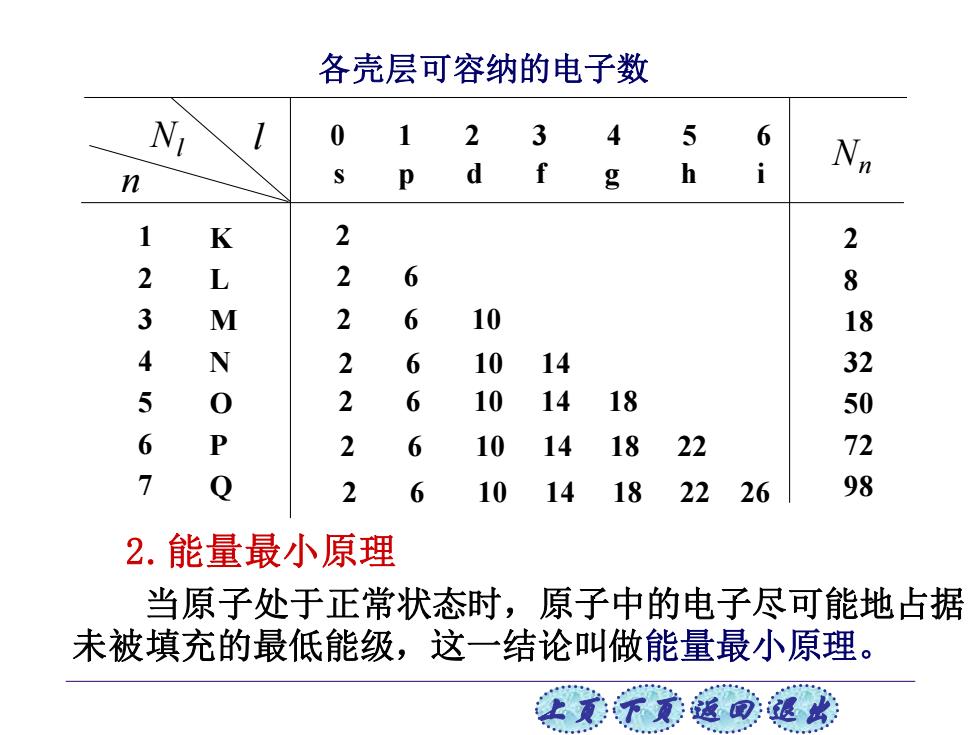
各壳层可容纳的电子数 N 0 2 5 6 p d f h Nn 1 K 2 2 2 L 2 6 8 3 M 2 6 10 18 4 N 2 6 10 14 32 5 2 6 10 14 18 50 6 P 2 6 10 14 18 22 72 7 Q 2 6 10 14 18 22 26 98 2.能量最小原理 当原子处于正常状态时,原子中的电子尽可能地占据 未被填充的最低能级,这一结论叫做能量最小原理。 让意不意返回退
上页 下页 返回 退出 各壳层可容纳的电子数 0 1 2 3 4 5 6 s p d f g h i 1 2 3 4 5 6 7 K L M N O P Q 2 2 6 2 6 10 2 6 10 14 2 6 10 14 18 2 6 10 14 18 22 2 6 10 14 18 22 26 Nn 2 8 18 32 50 72 98 l n Nl 2.能量最小原理 当原子处于正常状态时,原子中的电子尽可能地占据 未被填充的最低能级,这一结论叫做能量最小原理

例题13-19分别计算量子数n=2、=1和n=2的电子的可 能状态数。 解:对n=2、=1的电子,可取m后-1,0,1三种状态, 对每一种m,又可取m,1/2,-1/2。故总的状态 数为 3×2=6 对于n=2的电子,1可取0和1。 1=0时,→m0,m,=1/2,-1/2 →=0时,有2种状态。 因此,共有状态数2+6=8。 让美下觉返司速此
上页 下页 返回 退出 例题13-19 分别计算量子数n=2、l=1和n=2的电子的可 能状态数。 解: 对n=2、l=1的电子,可取ml=-1,0,1三种状态, 对每一种ml,又可取ms=1/2,-1/2。故总的状态 数为 32 = 6 对于n=2的电子,l 可取0和1。 l=0时, ml=0,ms=1/2, -1/2 l=0时,有2种状态。 因此,共有状态数 2+6=8

选择进入下一节 §13-0 教学基本要求 §13-1 热辐射普朗克的能量子假设 §13-2 光电效应爱因斯坦的光子理论 §13-3 康普顿效应 §13-4 氢原子光谱 玻尔的氢原子理论 §13-5 德布罗意波 微观粒子的波粒二象性 §13-6 不确定关系 §13-7 波函数及其统计诠释薛定谔方程 §13-8 一维定态薛定谔方程的应用 §13-9 量子力学中的氢原子问题 §13-10电子的自旋原子的电子壳层结构
上页 下页 返回 退出 选择进入下一节 §13-0 教学基本要求 §13-1 热辐射 普朗克的能量子假设 §13-2 光电效应 爱因斯坦的光子理论 §13-3 康普顿效应 §13-4 氢原子光谱 玻尔的氢原子理论 §13-5 德布罗意波 微观粒子的波粒二象性 §13-6 不确定关系 §13-7 波函数及其统计诠释 薛定谔方程 §13-8 一维定态薛定谔方程的应用 §13-9 量子力学中的氢原子问题 §13-10 电子的自旋 原子的电子壳层结构