
§12-4光程与光程差 一、光程 半相位差在分析光的干涉时十分重要,为 便于计算光通过不同介质时的相位差, 引入“光程”的概念。 米光在介质中传播时,光振动的相位沿传播 方向逐点落后。光传播一个波长的距离, 相位变化2π。 让意不意适回退块
上页 下页 返回 退出 相位差在分析光的干涉时十分重要,为 便于计算光通过不同介质时的相位差, 引入“光程”的概念。 光在介质中传播时,光振动的相位沿传播 方向逐点落后。光传播一个波长的距离, 相位变化2。 一、 光 程 §12-4 光程与光程差
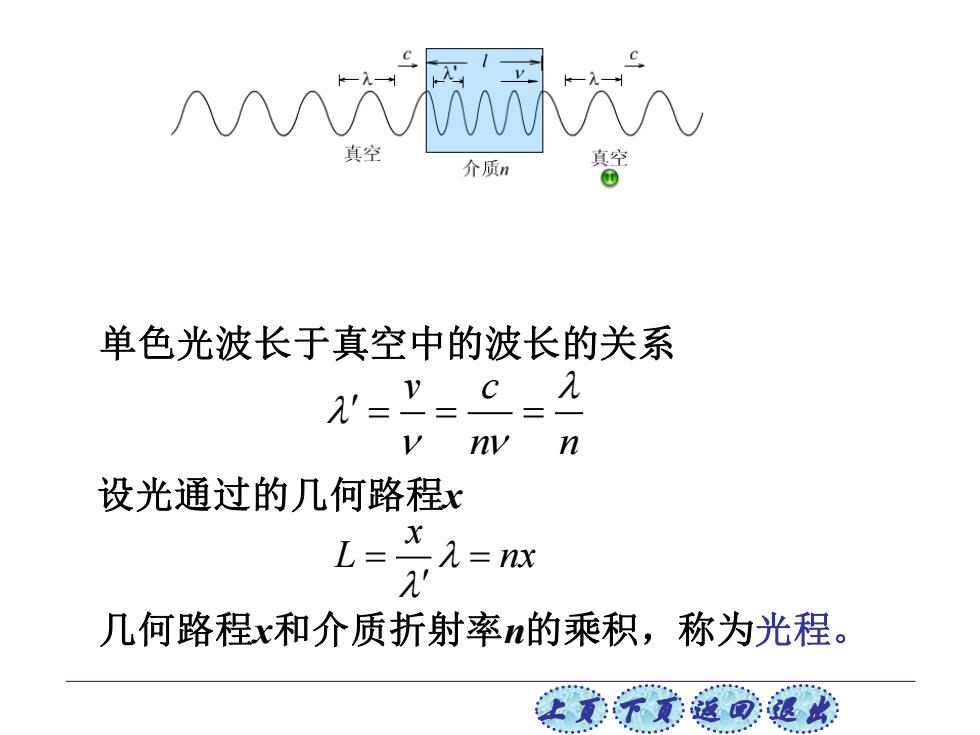
大丽 介质n 单色光波长于真空中的波长的关系 '=y=C= v ny n 设光通过的几何路程x L=- X 几何路程x和介质折射率n的乘积,称为光程。 让美下元返回:退欢
上页 下页 返回 退出 单色光波长于真空中的波长的关系 v c n n = = = 设光通过的几何路程x x L nx = = 几何路程x和介质折射率n的乘积,称为光程

二、光程差 2π2」 2元ri S △功= 入2 入 nj n2 2元n2h22πn1i 2入0 入0 2π(0n22-n,i) 光程差: δ=n2r2-ni 40s 2I6 相位差和光程差的关系: 10 让意了意适回退块
上页 下页 返回 退出 相位差和光程差的关系: r1 r2 S1 S2 n1 n2 P 光程差: 二、光程差 0 2 = π

例题12-8如图,在S,P间插入折射率为、厚度为 d的介质。求:光由S1、S2到P的相位差△中。 解: 2(2-1) (n-d)+nd]-n) 2[&-*a-)] 让美下觉返司速此
上页 下页 返回 退出 · S1 S2 r1 r2 d n P 解: 例题12-8 如图,在S2P 间插入折射率为n、厚度为 d 的介质。求:光由S1、S2 到 P 的相位差
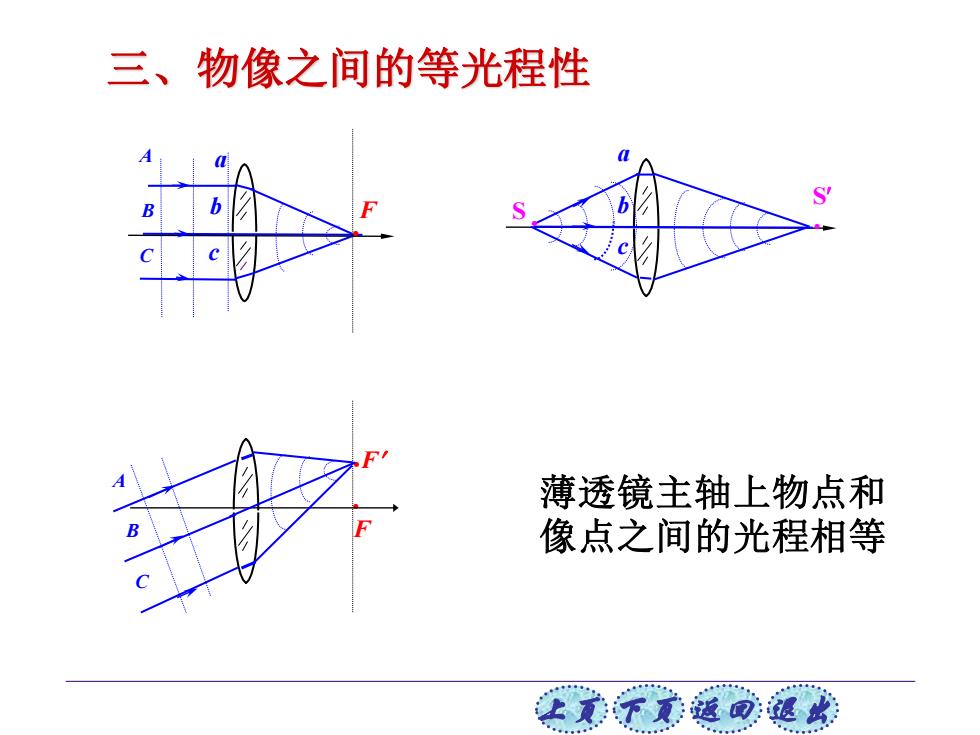
三、物像之间的等光程性 薄透镜主轴上物点和 像点之间的光程相等 上意不家返可退此
上页 下页 返回 退出 S a c b · · S · ·F A B C F · F A B C a b c 三、物像之间的等光程性 薄透镜主轴上物点和 像点之间的光程相等

四、反射光的相位突变和附加光程差 反射光有元相位突变,称半波损失,它相当于一 个附加光程差: 6= 2 发生附加光程差的条件: n1n3或n1>n2<n3 n3 让美下觉返同速
上页 下页 返回 退出 发生附加光程差的条件: n3 n1 n2 1 2 n1 n3 或 n1 >n2<n3 反射光有 相位突变,称半波损失,它相当于一 个附加光程差: 2 = 四、反射光的相位突变和附加光程差

选择进入下一节 §12-0教学基本要求 *§12-1几何光学简介 §12-2光源单色光相干光 §12-3双缝干涉 §124光程与光程差 §12-5薄膜干涉 *§12-6迈克耳孙干涉仪 §12-7光的衍射现象惠更斯-菲涅耳原理 §12-8单缝的夫琅禾费衍射 让意不意通可退欢
上页 下页 返回 退出 选择进入下一节 §12-0 教学基本要求 *§12-1 几何光学简介 §12-2 光源 单色光 相干光 §12-3 双缝干涉 §12-4 光程与光程差 §12-5 薄膜干涉 *§12-6 迈克耳孙干涉仪 §12-7 光的衍射现象 惠更斯-菲涅耳原理 §12-8 单缝的夫琅禾费衍射

§129圆孔的夫琅禾费衍射光学仪器的分辨本领 §12-10光栅衍射 *§12-11X射线的衍射 §12-12光的偏振状态 §12-13起偏和检偏马吕斯定律 §12-14反射和折射时光的偏振 *§12-15光的双折射 *§12-16偏振光的干涉人为双折射 *§12-17旋光性 *§12-18现代光学简介 让美觉返司退
上页 下页 返回 退出 §12-9 圆孔的夫琅禾费衍射 光学仪器的分辨本领 §12-10 光栅衍射 *§12-11 X射线的衍射 §12-12 光的偏振状态 §12-13 起偏和检偏 马吕斯定律 §12-14 反射和折射时光的偏振 *§12-15 光的双折射 *§12-16 偏振光的干涉 人为双折射 *§12-17 旋光性 *§12-18 现代光学简介