
§11-4波的能量波的强度 弹性波传播到介质中的某处,该处将具有动能和势 能。在波的传播过程中,能量从波源向外传播。 正意子元道回退此
上页 下页 返回 退出 弹性波传播到介质中的某处,该处将具有动能和势 能。在波的传播过程中,能量从波源向外传播。 §11-4 波的能量 波的强度

一、波的能量 考虑介质中的体积△V,其质量为△m(△m=pAV)。当 波动传播到该体积元时,将具有动能△E和弹性势能△E。 平面简谐 支x,)=Acos - 有如下关系: AE-AE,-(AV)sin -9 +40 u 让意文滋可退攻
上页 下页 返回 退出 0 ( , ) cos x y x t A t u = − + 平面简谐波 2 2 2 0 1 ( )sin 2 x E E A V t u = = − + k p 有如下关系: 一、波的能量 波动传播到该体积元时,将具有动能 Ek 和弹性势能 Ep 考虑介质中的体积V,其质量为 m(m=V ) 。当
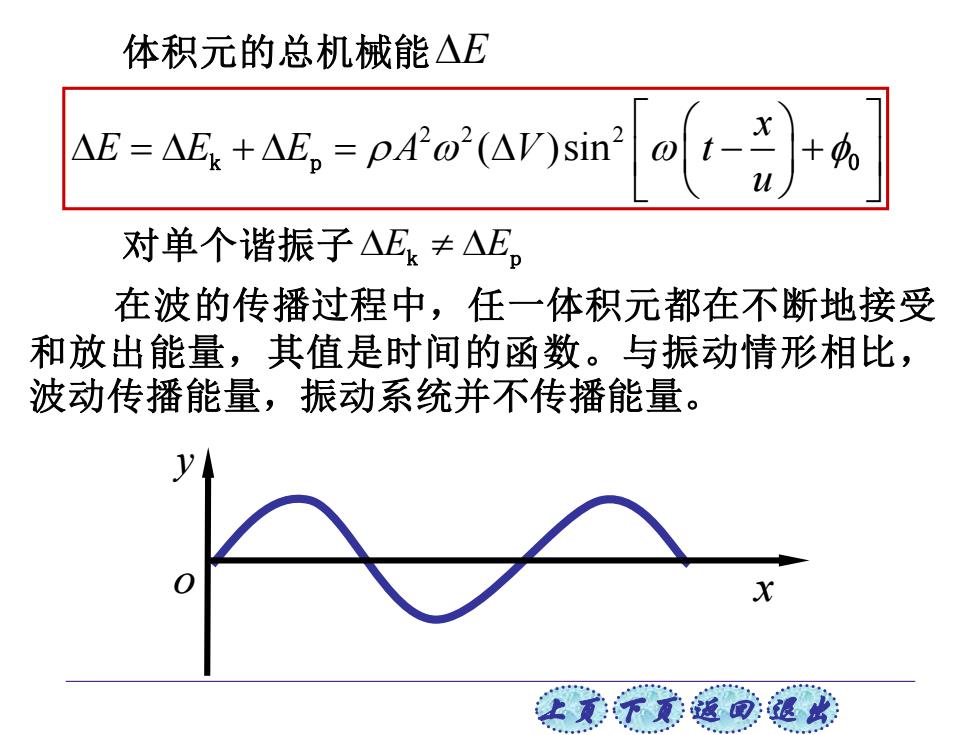
体积元的总机械能△E +NE,-po (AV)sin + 对单个谐振子△E≠△E, 在波的传播过程中,任一体积元都在不断地接受 和放出能量,其值是时间的函数。与振动情形相比, 波动传播能量,振动系统并不传播能量。 让意子意返回退收
上页 下页 返回 退出 对单个谐振子 E E k p 在波的传播过程中,任一体积元都在不断地接受 和放出能量,其值是时间的函数。与振动情形相比, 波动传播能量,振动系统并不传播能量。 体积元的总机械能 E 2 2 2 ( )sin x E E E A V t u = + = − + k p 0 y o x
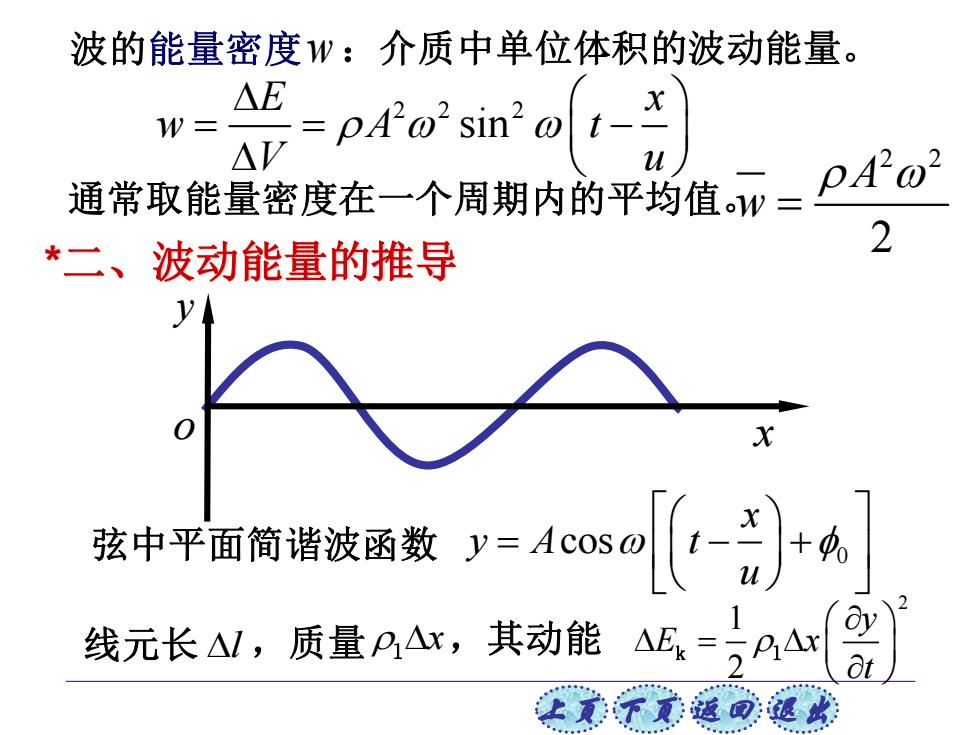
波的能量密度w:介质中单位体积的波动能量。 g=是=p.Pwsiwo到 △E 通常取能量密度在一个周期内的平均值,p=P10 *二、波动能量的推导 2 孩中斗国情谐泼国数ycs0[(+A] 线元长M,质量AA,其动能A=DAr 让美下觉返司速此
上页 下页 返回 退出 *二、波动能量的推导 y o x 弦中平面简谐波函数 0 cos x y A t u = − + 线元长 l ,质量 x l ,其动能 2 1 2 y E x t = k l 2 2 2 sin E x w A t V u = = − 通常取能量密度在一个周期内的平均值。 2 2 2 A w = 波的能量密度 w :介质中单位体积的波动能量

势能 AE,=F(△1-△x) △x很小时 s-ww心-a-定 △x 机械能 2 AF=AEX+AE,=2A (
上页 下页 返回 退出 势能 = − E F l x ( ) p x 很小时 1 2 2 2 2 2 1 ( ) ( ) 1 1 2 y y l x y x x x x = + = + + 2 1 2 y E F x x = p 2 2 1 1 2 2 y y E E E x F x x x = + = + k p l 机械能

对于平面简谐波 1 1 AE=FAx 2 由于u= 〉△E=AE。 A=Fmo-引+ 同样可求能量密度。 让美下觉返同速
上页 下页 返回 退出 对于平面简谐波 2 2 2 2 0 1 1 sin 2 2 y x E x x A t t u = = − + k l l 2 2 2 2 2 0 1 1 1 sin 2 2 y x E F x F x A t t u u = = − + p 由于 F u = l = E E k p 2 2 2 0 sin x E x A t u = − + l 同样可求能量密度
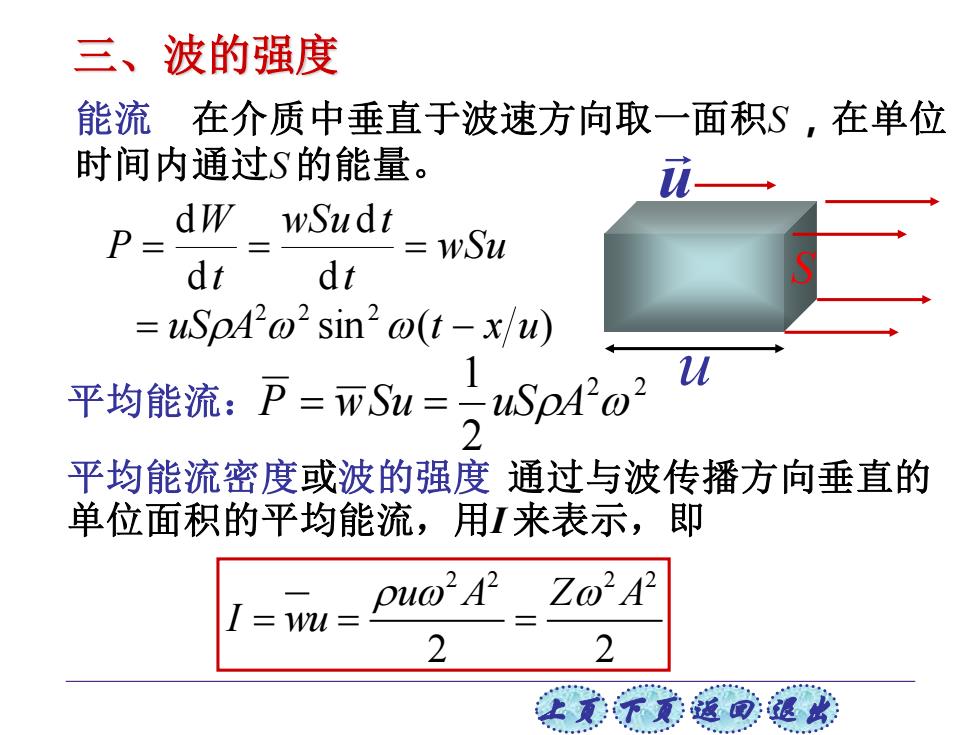
三、波的强度 能流 在介质中垂直于波速方向取一面积S,在单位 时间内通过S的能量。 P dw wSudt wSu dt dt uSpA'o'sin2o(t-x/u) 平均能流:P=wSu=。uSp4w2 平均能流密度或波的强度通过与波传播方向垂直的 单位面积的平均能流,用I来表示,即 I=wu= puo'A ZOA 2 2 上美不意通可退
上页 下页 返回 退出 能流 在介质中垂直于波速方向取一面积S ,在单位 时间内通过S 的能量。 u S u wSu t wSu t t W P = = = d d d d sin ( ) 2 2 2 = uSA t − x u 平均能流: 2 2 2 1 P = wSu = uSA 平均能流密度或波的强度 通过与波传播方向垂直的 单位面积的平均能流,用I 来表示,即 2 2 2 2 2 2 u A Z A I wu = = = 三、波的强度

介质的特性阻抗Z=pu。 I的单位:W.m2(瓦特/米2) 平面余弦行波振幅不变的意义: y=Acoso (t-x/u) R=mas=5时a2S月=属s=4o7s 若P=P有A,=A, 让美觉返司退
上页 下页 返回 退出 介质的特性阻抗 Z u = 。 I 的单位: W.m-2 (瓦特/米2 ) 平面余弦行波振幅不变的意义: y = Acos (t − x u) u S A1 S A2 P wuS A uS 2 2 1 1 1 2 1 = = P w uS A uS 2 2 2 2 2 2 1 = = 若P1 = ,有P2 A。 1 = A2

对于球面波,S,=42,S2=4π2,介质不吸收能量 时,通过两个球面的总能流相等 3pfoiuwi-pio'wdr 1 4=2 A 球面波表达式: 式中A为波在离原点单位距离处振幅的数值。 让意不意适回退收
上页 下页 返回 退出 2 2 2 2 2 2 1 1 2 2 1 1 4π 4π 2 2 A u r A u r = 时,通过两个球面的总能流相等 1 2 2 1 A r A r = 球面波表达式: 0 0 0 cos ( ) A r r t r u = − − 式中 A r0 0 为波在离原点单位距离处振幅的数值。 对于球面波, , ,介质不吸收能量 2 2 2 S r = 4π 2 1 1 S r = 4π

例题115用聚焦超声波的方式,可以在液体 中产生强度达120kW/cm的大振幅超声波。设 波源作简谐振动,频率为500kHz,液体的密度 为1g/cm3,声速为1500m/s,求这时液体质点振 动的振幅。 解:因I=pu4o2/2,所以 21 =1.27×10-5m 可见液体中声振动的振幅实际上是极小的。 让美下元返回退欢
上页 下页 返回 退出 例题11-5 用聚焦超声波的方式,可以在液体 中产生强度达120kW/cm2的大振幅超声波。设 波源作简谐振动,频率为500kHz,液体的密度 为1g/cm3,声速为1500m/s,求这时液体质点振 动的振幅。 解:因 I = uA2 2 2 ,所以 可见液体中声振动的振幅实际上是极小的。 1 2 5 1.27 10 m I A pu − = =