§11-3 波动方程波速 一、波动方程 对y=4年4求xf的二阶偏导数,得到 o 812 -A 平面波的波 &x2 u2 812 动微分方程 江觉不返回退球
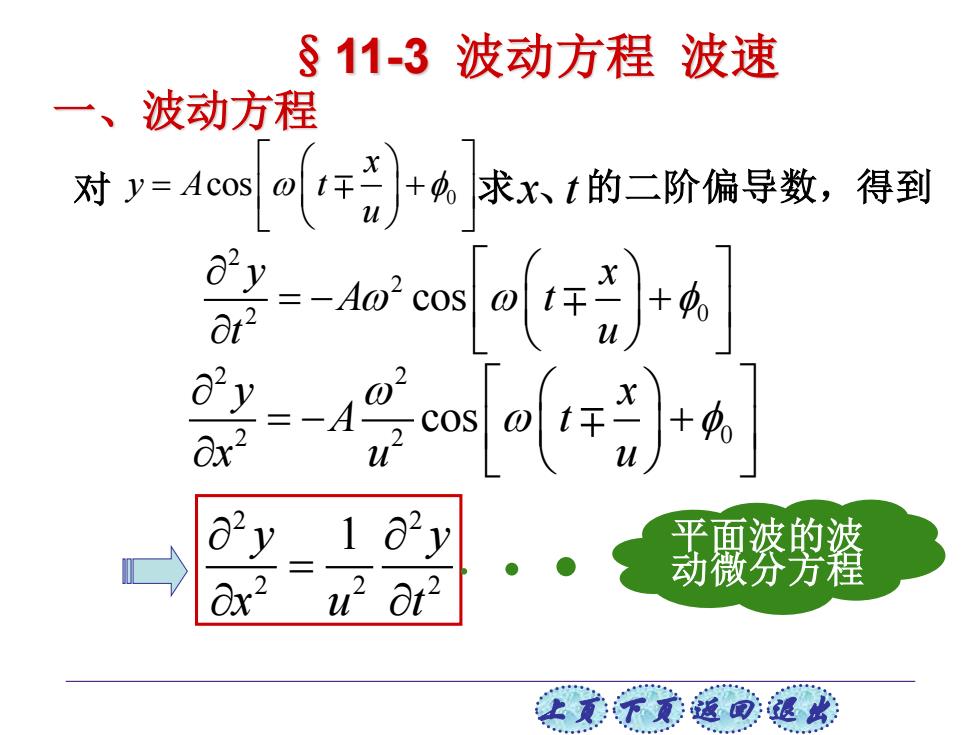
上页 下页 返回 退出 2 2 2 0 cos y x A t t u = − + 2 2 2 2 2 y y 1 x u t = 平面波的波 动微分方程 2 2 2 2 0 cos y x A t x u u = − + §11-3 波动方程 波速 一、波动方程 0 cos x y A t u = + 对 求 x t 、 的二阶偏导数,得到
*二、波动方程的建立 在张力为张紧的无限长弦上施加横向扰动,产生横波 张力不变 F F=F=F 合力 ∑F=Fsine。-Fsine。=F(sine。-sine.) 让意了京适可:退此
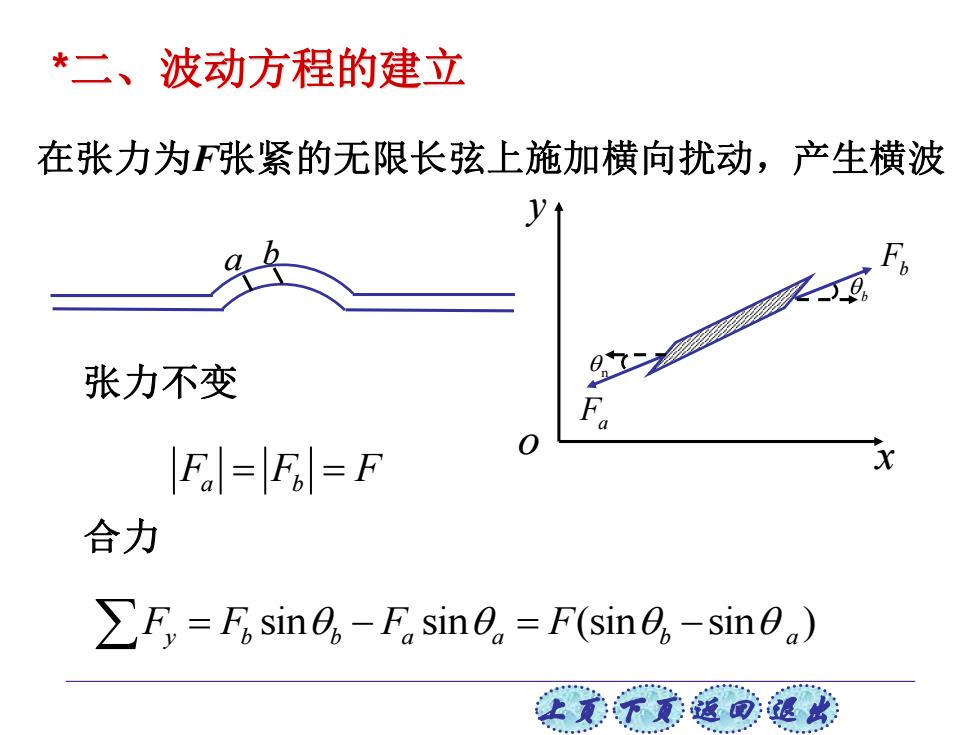
上页 下页 返回 退出 *二、波动方程的建立 b n Fb F a x y o 在张力为F张紧的无限长弦上施加横向扰动,产生横波 a b F F F a b = = 张力不变 合力 sin sin (sin sin ) F F F F y b b a a b a = − = −

对于微小扰动sin0,=tanB,sin0,=tan8 而且tan0= 可得 r2 由牛顿定律,可得 0"y ∑E,=mia,=DA oyeo'y F 〉波速 u= Ox2 F8t2 P 让意下式返回:退
上页 下页 返回 退出 对于微小扰动 sin tan sin tan a a b b = = , 而且 tan y x = 可得 2 y 2 b a y y y F F F x x x x = − = 由牛顿定律,可得 2 y y l 2 y F ma x x = = 2 2 2 2 l y y x F t = 波速 l F u =

三、波速 柔软细绳和弦中横波 u E 固体内纵波 u 固体内横波 E固体杨氏模量,G剪切模量,P密度
上页 下页 返回 退出 柔软细绳和弦中横波 三、波速 l F u = 固体内纵波 E u = 固体内横波 G u = E 固体杨氏模量,G 剪切模量, 密度
*四、介质的形变及其模量 1.线变 截面积S,正应力了,线应变 实验表明,在弹性范围内 E为杨氏模量 让文不美蕴回蕴以
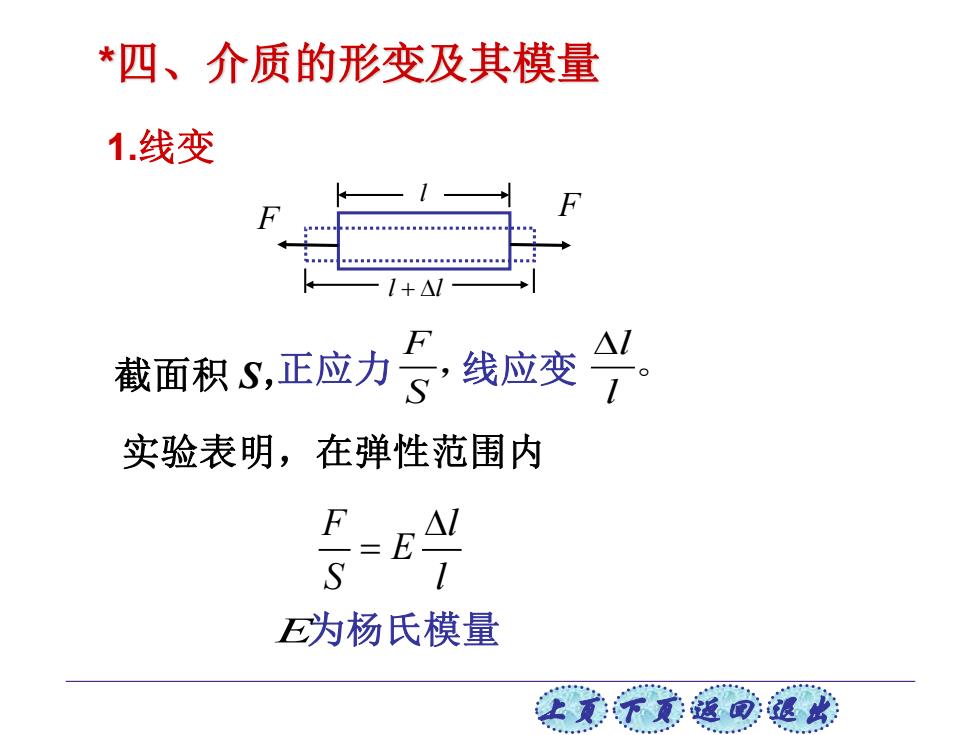
上页 下页 返回 退出 *四、介质的形变及其模量 1.线变 F l l + l F 截面积 S,正应力 F S , 线应变 l l 。 实验表明,在弹性范围内 F l E S l = E 为杨氏模量
2.体变 压强增量与体积增量成正比 为体积模量 上美不返可退此
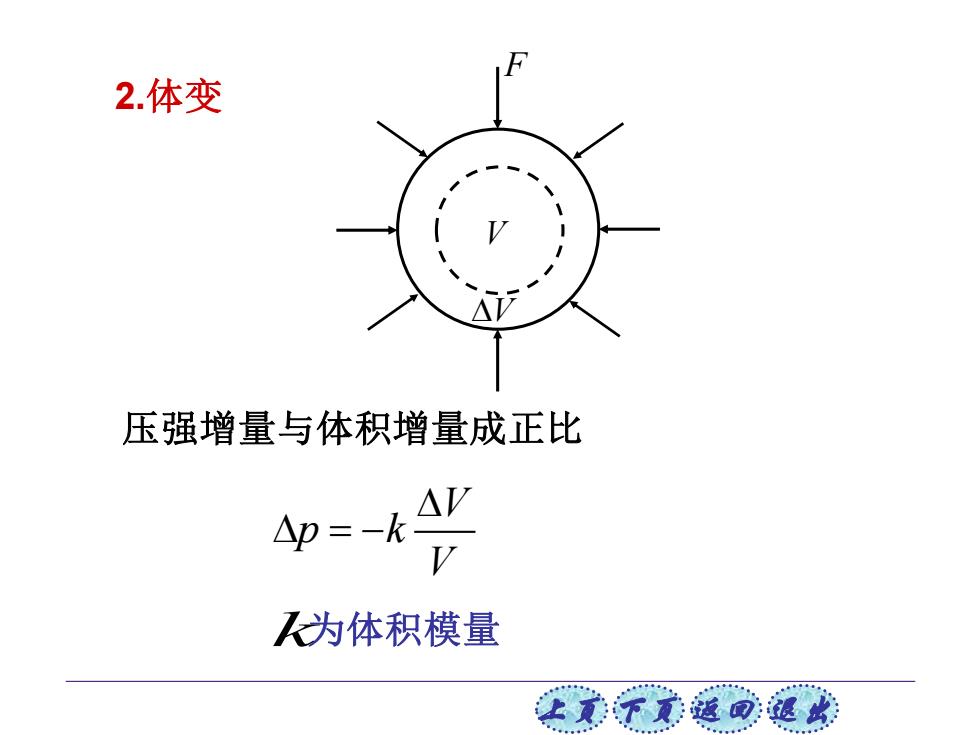
上页 下页 返回 退出 2.体变 F V V 压强增量与体积增量成正比 V p k V = − k 为体积模量
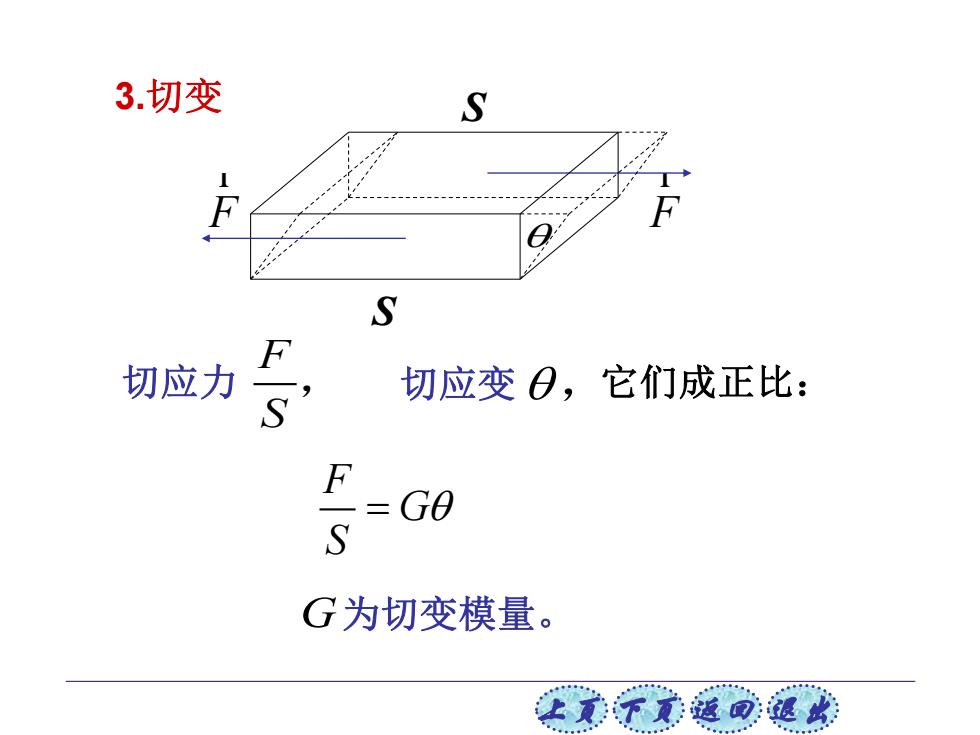
3.切变 S 切应力 切应变0,它们成正比: F =G0 S G为切变模量。 让美觉返司退
上页 下页 返回 退出 3.切变 F r F r S S 切应力 F S , 切应变 , 它们成正比: F G S = G 为切变模量

选择进入下一节 §11-0 教学基本要求 §11-1机械波的产生和传播 §11-2 平面简谐波的波函数 §11-3 波动方程波速 §11-4 波的能量 波的强度 *§11-5 声波 超声波 次声波 §11-6 电磁波 §11-7 惠更斯原理 波的衍射反射和折射 §11-8 波的叠加原理 波的干涉! 驻波 §11-9 多普勒效应 让意不意适回退块
上页 下页 返回 退出 选择进入下一节 §11-0 教学基本要求 §11-1 机械波的产生和传播 §11-2 平面简谐波的波函数 §11-3 波动方程 波速 §11-4 波的能量 波的强度 *§11-5 声波 超声波 次声波 §11-6 电磁波 §11-7 惠更斯原理 波的衍射 反射和折射 §11-8 波的叠加原理 波的干涉 驻波 §11-9 多普勒效应