
§10-3 受迫振动 共振 一、受迫振动 物体在周期性外力的持续作用下发生的振动 称为受迫振动。 物体所受驱动力:F=Fc0Sot 运动方程: x=-a-ydt d2 dxFcost 令 k2 ,Y=26 m d2x +26 dx dt2 +0x= dt m 让贰不元通回退欢
上页 下页 返回 退出 物体在周期性外力的持续作用下发生的振动 称为受迫振动。 一、受迫振动 §10-3 受迫振动 共振 物体所受驱动力: 运动方程: 令 2 m = 0 d F F t = cos 2 2 0 d d cos d d x x m kx F t t t = − − + 2 0 k m = , 2 2 0 2 0 d d d 2 cos d d x x F x t t t m + + =
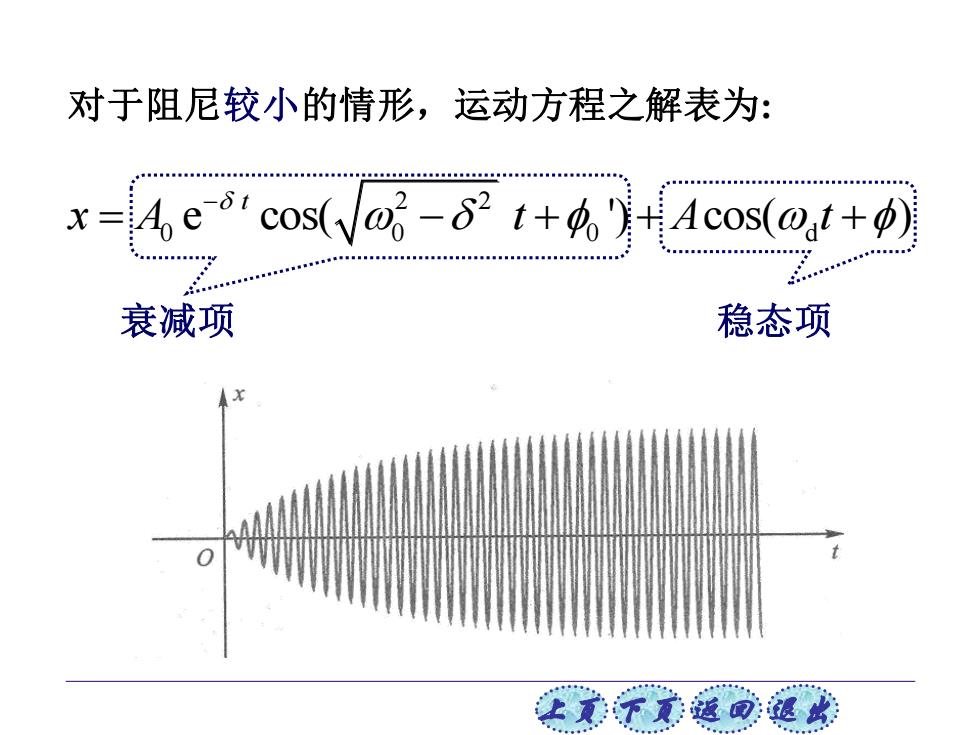
对于阻尼较小的情形,运动方程之解表为: x=ecos(-2Acos(t+ 衰减项 稳态项 让美觉返司退
上页 下页 返回 退出 对于阻尼较小的情形,运动方程之解表为: 衰减项 稳态项 2 2 0 0 0 d e cos( ') cos( ) t x A t A t − = − + + +

经过一段时间后,衰减项忽略不计,仅考虑稳态项: x=Acos(@t+) F →= 260: m√o-o2+4o2a tanΦ= 稳态时振动物体速度: V= =cos((@,+p+2) dx dt @F 式中 Vm= mV(@-o)2+482o好 在受迫振动中,周期性的驱动力对振动系统提供 能量,另一方面系统又因阻尼而消耗能量,若二者相 等,则系统达到稳定振动状态
上页 下页 返回 退出 0 2 2 2 2 2 0 d d , ( ) 4 F A m = − + d 2 2 0 d 2 tan = − − 稳态时振动物体速度: 在受迫振动中,周期性的驱动力对振动系统提供 能量,另一方面系统又因阻尼而消耗能量,若二者相 等,则系统达到稳定振动状态。 m d d π cos( ) d 2 x v v t t = = + + 式中 0 m 2 2 2 2 2 0 d d ( ) 4 F v m = − + 经过一段时间后,衰减项忽略不计,仅考虑稳态项: d x A t = + cos( )
二、共振 对于受迫振动,当外力幅值恒定时,稳定态 振幅随驱动力的频率而变化。当驱动力的角频率 等于某个特定值时,位移振幅达到最大值的现象 称为位移共振。 共振现象 让美下觉返司速此
上页 下页 返回 退出 对于受迫振动,当外力幅值恒定时,稳定态 振幅随驱动力的频率而变化。当驱动力的角频率 等于某个特定值时,位移振幅达到最大值的现象 称为位移共振。 二、共 振
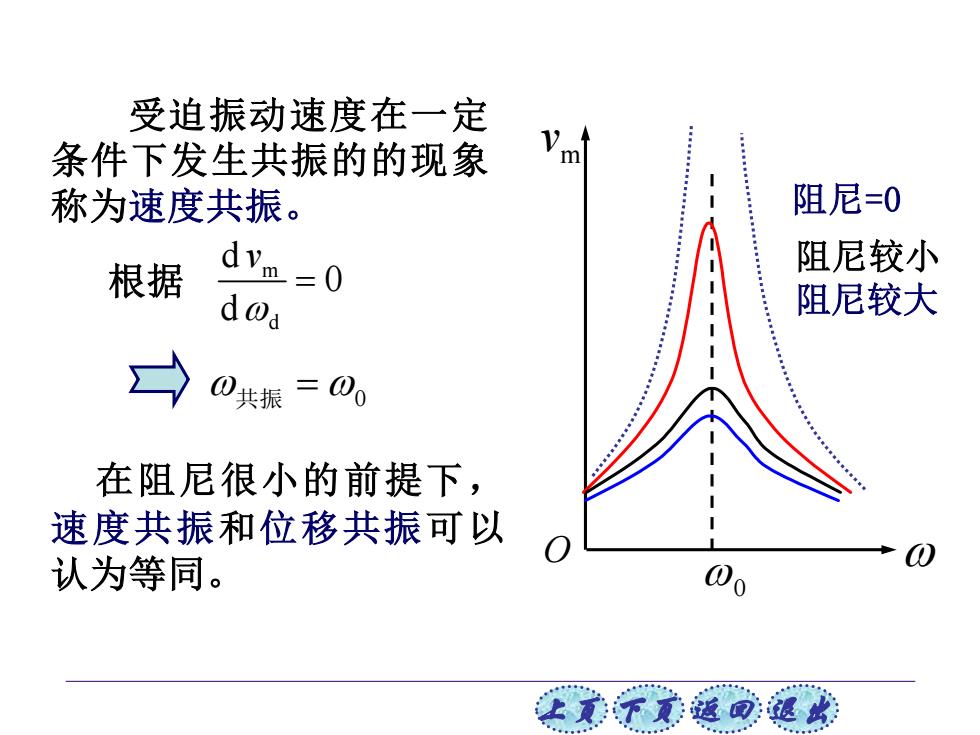
受迫振动速度在一定 条件下发生共振的的现象 Vm 称为速度共振。 阻尼=0 根据 dvm二0 阻尼较小 d@s 阻尼较大 〉 0共振=00 在阻尼很小的前提下, 速度共振和位移共振可以 认为等同。 00 上意不家返可退此
上页 下页 返回 退出 受迫振动速度在一定 条件下发生共振的的现象 称为速度共振。 根据 在阻尼很小的前提下, 速度共振和位移共振可以 认为等同。 m v O 0 阻尼=0 阻尼较小 阻尼较大 m d d 0 d v = 共振 = 0

共振的应用和防止 应用 共振筛 共鸣箱 防止 1.队列或火车过桥时要便步走或放慢速度 2.在振动物体底座加防振垫 3.装修剧场、房屋时使用吸声材料等 上文不美返回退球
上页 下页 返回 退出 共振的应用和防止 共振筛 共鸣箱 应用 防止 1.队列或火车过桥时要便步走或放慢速度 2.在振动物体底座加防振垫 3.装修剧场、房屋时使用吸声材料等

选择进入下一节 §10-0 教学基本要求 §10-1 谐振动 §10-2 阻尼振动 §10-3 受迫振动 共振 §10-4 电磁振荡 §10-5 一维谐振动的合成 *§10-6 二维谐振动的合成 *§10-7 振动的分解频谱 *§10-8 非线性振动与混沌 正意子元道回退此
上页 下页 返回 退出 选择进入下一节 §10-0 教学基本要求 §10-1 谐振动 §10-2 阻尼振动 §10-3 受迫振动 共振 §10-4 电磁振荡 §10-5 一维谐振动的合成 *§10-6 二维谐振动的合成 *§10-7 振动的分解 频谱 *§10-8 非线性振动与混沌