
§11-8波的叠加原理波的干涉驻波 一、波的叠加原理 波传播的独立性:几个波源产生的波,同时在一 介质中传播,如果这几列波在空间某点处相遇,那么 每一列波都将独立地保持自己原有的特性(频率、波 长、振动方向等)传播。 让美觉返司退
上页 下页 返回 退出 波传播的独立性: 几个波源产生的波,同时在一 介质中传播,如果这几列波在空间某点处相遇,那么 每一列波都将独立地保持自己原有的特性(频率、波 长、振动方向等)传播。 §11-8 波的叠加原理 波的干涉 驻波 一、波的叠加原理
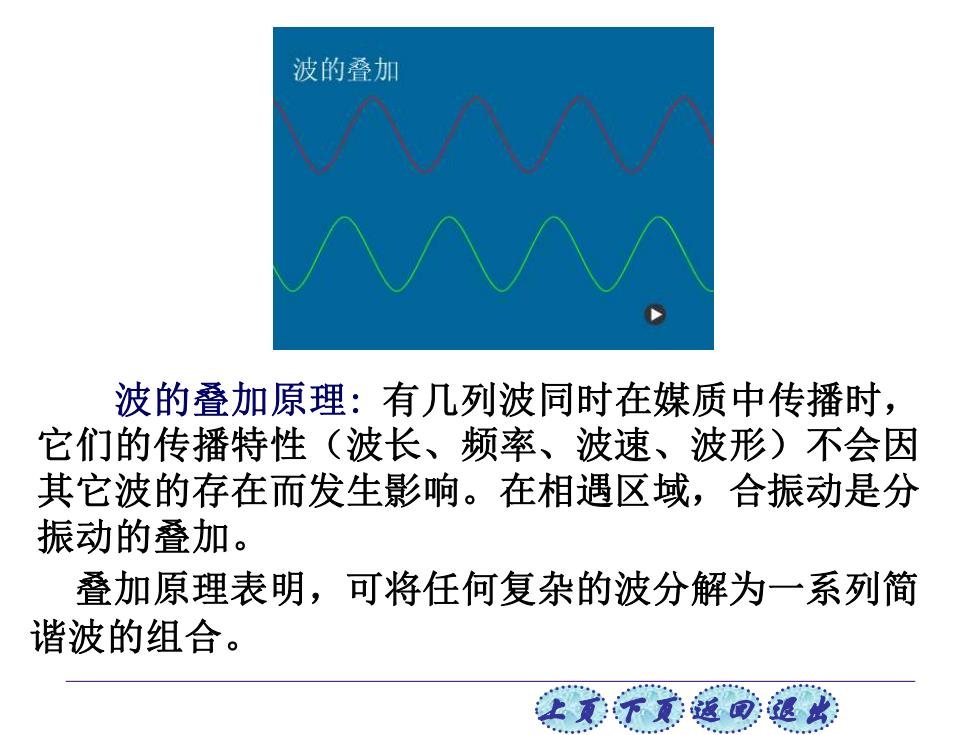
波的叠加 波的叠加原理:有几列波同时在煤质中传播时, 它们的传播特性(波长、频率、波速、波形)不会因 其它波的存在而发生影响。在相遇区域,合振动是分 振动的叠加。 叠加原理表明,可将任何复杂的波分解为一系列简 谐波的组合
上页 下页 返回 退出 波的叠加原理: 有几列波同时在媒质中传播时, 它们的传播特性(波长、频率、波速、波形)不会因 其它波的存在而发生影响。在相遇区域,合振动是分 振动的叠加。 叠加原理表明,可将任何复杂的波分解为一系列简 谐波的组合

二、波的干涉 相干波 相干条件:。振动方向相同 。频率相同 。相位相同或相位差恒定 相干波:满足相干条件的几列波称为相干波。 相干波源:能发出相干波的波源称为相干波源。 让美下觉返司速此
上页 下页 返回 退出 相干波 相干条件: 振动方向相同 频率相同 相位相同或相位差恒定 相干波:满足相干条件的几列波称为相干波。 相干波源:能发出相干波的波源称为相干波源。 二、波的干涉
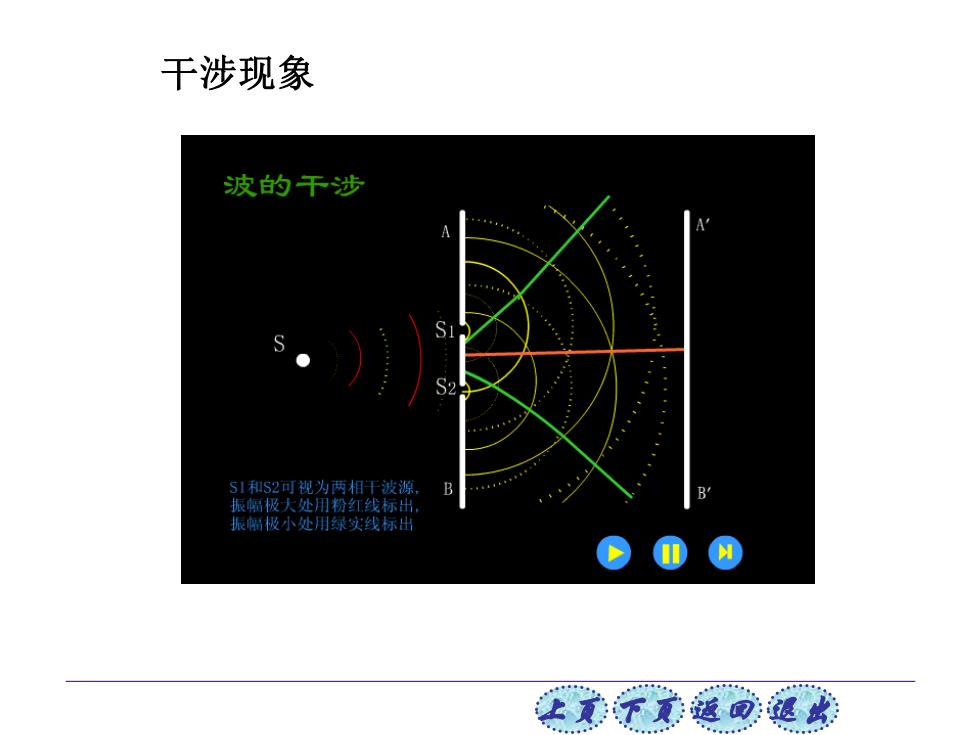
干涉现象 波的干涉 51和S2可视为两相干波源 振幅极大处用粉红线标出 振幅极小处用绿实线标出 让意不家返可退此
上页 下页 返回 退出 干涉现象

强弱分布规律 两个相干波源波源S, 和S,的振动方程分别为 S SP=n s1=A0c0s(0t+40) s2=A20C0s(0t+0) S29 S2P=3 S,和S,单独存在时,在P点引起的振动的方程为 乃=月c0s(o1+4。-2) 片=4c0s(or+4,2 让美下觉返同速
上页 下页 返回 退出 强弱分布规律 1 S 2 S P 1 1 S P = r 2 2 S P = r 两个相干波源波源S1 和 S2的振动方程分别为 1 10 10 cos( ) S y A t = + 2 20 20 cos( ) S y A t = + S1和S2单独存在时,在P点引起的振动的方程为 1 1 1 10 2 cos( ) r y A t = + − π 2 2 2 20 2 cos( ) r y A t = + − π

P点的合方程为 y=+y2=Acos(at+) 振幅A和相位, A=V4+A6+2A4c0s[4o-4。-2π(2-5)/] πr2 +4sin-元 tan d 2 对于P点△中=40-40-2π(-)/九为常量, 因此A也是常量,并与P点空间位置密切相关。 上元子元返回退
上页 下页 返回 退出 P 点的合方程为 cos( ) = 1 + 2 = +0 y y y A t 2 2 1 2 1 2 20 10 2 1 A A A A A r r = + + − − − 2 cos 2 π( ) 振幅A和相位0 1 2 1 10 2 20 0 1 2 1 10 2 20 2π 2π sin sin tan 2π 2π cos cos r r A A r r A A − + − = − + − 对于P点 = − − − 20 10 2 1 2π( ) r r 为常量, 因此A 也是常量,并与P点空间位置密切相关

△0=中20-40 2r(=D=2kk=0,±1,±2,. λ A=A+A,(合振幅最大) △0=40-40 2-2=2k+10mk=0,±1,±2, 4=4-4 (合振幅最小) ○当△为其他值时,合振幅介于 A=A+A和A=41-A2之间 若4040'上述条件简化为 δ=片-3=k九,k=0,±1,±2,.(合振幅最大) ò=行-专-(+月2,k=0+1,+2(合振橱及小) 让美下元返回:退欢
上页 下页 返回 退出 A = A1 + A2 (合振幅最大) A = A1 − A2 (合振幅最小) 当 为其他值时,合振幅介于 若10 =20,上述条件简化为 1 2 = − r r k = , 0, 1, 2, k = 1 2 , 0, 1 1 2 r r k k , 2, = − = + = (合振幅最大) (合振幅最小) 2 1 20 10 2 ( ) 2 r r k − = − − = π π k = 0, 1 2 , , 2 1 20 10 2 ( ) 2( 1) r r k − = − − = + π π k = 0, 1 2 , , A = A1 + A2 和 A = A1 − A2 之间

波程差6=了-乃 两列相干波源为同相位时,在两列波的叠加的区域 内,在波程差于零或等于波长的整数倍的各点,振幅 最大;在波程差等于半波长的奇数倍的各点,振幅最 小。 因I0A2=A+A+2AAc0S△p →I=I1+I2+2II2cos△0 若L=L,叠加后波的强度: 1=2I,[l+c0s(△0】=4Lcos2 2 △中=2kπ,I=4;△φ=(2k+1)π,I=0
上页 下页 返回 退出 1 2 波程差 = r − r 两列相干波源为同相位时,在两列波的叠加的区域 内,在波程差于零或等于波长的整数倍的各点,振幅 最大;在波程差等于半波长的奇数倍的各点,振幅最 小。 因 2 2 2 1 2 1 2 I A A A A A = + + 2 cos I = I 1 + I 2 + 2 I 1 I 2 cos 若I1 =I2,叠加后波的强度: 2 1 1 2 [1 cos( )] 4 cos 2 I I I = + = = 2k, I = 4I; = (2k +1) , I = 0
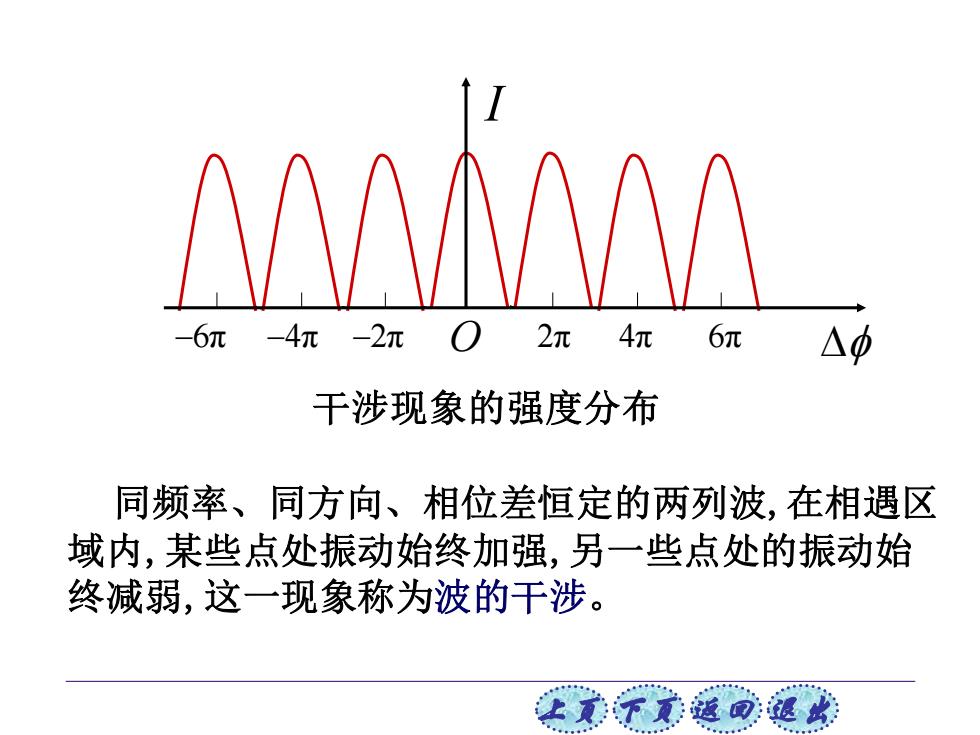
6π -4元-2π0 2π4π 6元 △功 干涉现象的强度分布 同频率、同方向、相位差恒定的两列波,在相遇区 域内,某些点处振动始终加强,另一些点处的振动始 终减弱,这一现象称为波的干涉。 让美下觉返司速此
上页 下页 返回 退出 同频率、同方向、相位差恒定的两列波,在相遇区 域内,某些点处振动始终加强,另一些点处的振动始 终减弱,这一现象称为波的干涉。 −6π −4π −2π O 2π 4π 6π I 干涉现象的强度分布
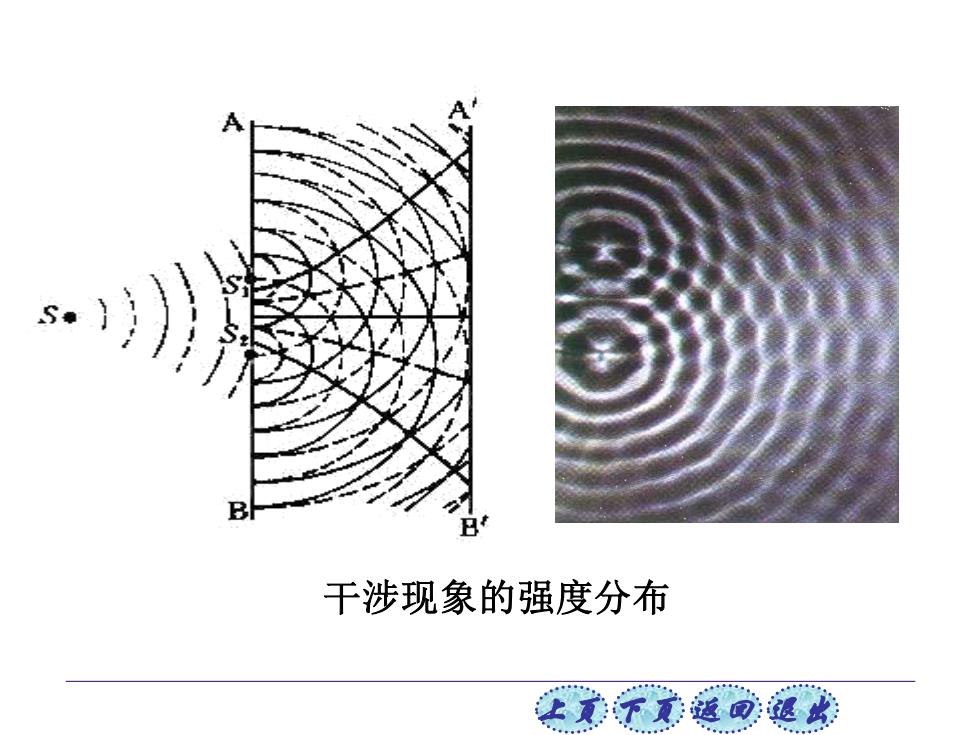
干涉现象的强度分布 让意了意通回蕴
上页 下页 返回 退出 干涉现象的强度分布