*§9-7电磁场的统一性和电磁场量的相对性 一、运动的相对性和电磁场的统一性 相对参考系静 电荷周围只 观察结 止的观察者考 有静电场 果的不 某参 察该电荷 同反映 了电磁 场的统 电荷 相对参考系匀 电荷周围有 一性和 直运动的观察 电场和磁场 相对性 者考察该电荷 让美下觉返司速此
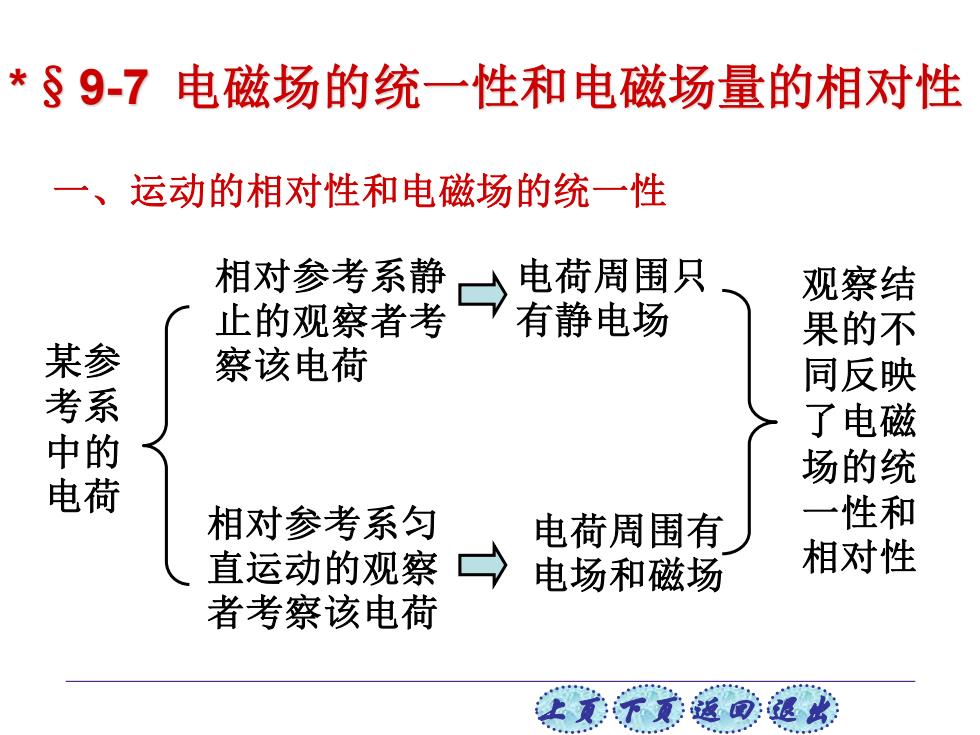
上页 下页 返回 退出 *§9-7 电磁场的统一性和电磁场量的相对性 一、运动的相对性和电磁场的统一性 某参 考系 中的 电荷 相对参考系静 止的观察者考 察该电荷 相对参考系匀 直运动的观察 者考察该电荷 电荷周围只 有静电场 电荷周围有 电场和磁场 观察结 果的不 同反映 了电磁 场的统 一性和 相对性
二、电磁场量的相对性 如图,设有两惯性系, K'相对于K以匀速v沿防 K V. 向运动。 电荷静止于K'系, K系中观察,产生了电 场E',更一般的情况下还 有B。 K系中观察,q产生了电场E 和磁场B。 上意不家返可退此
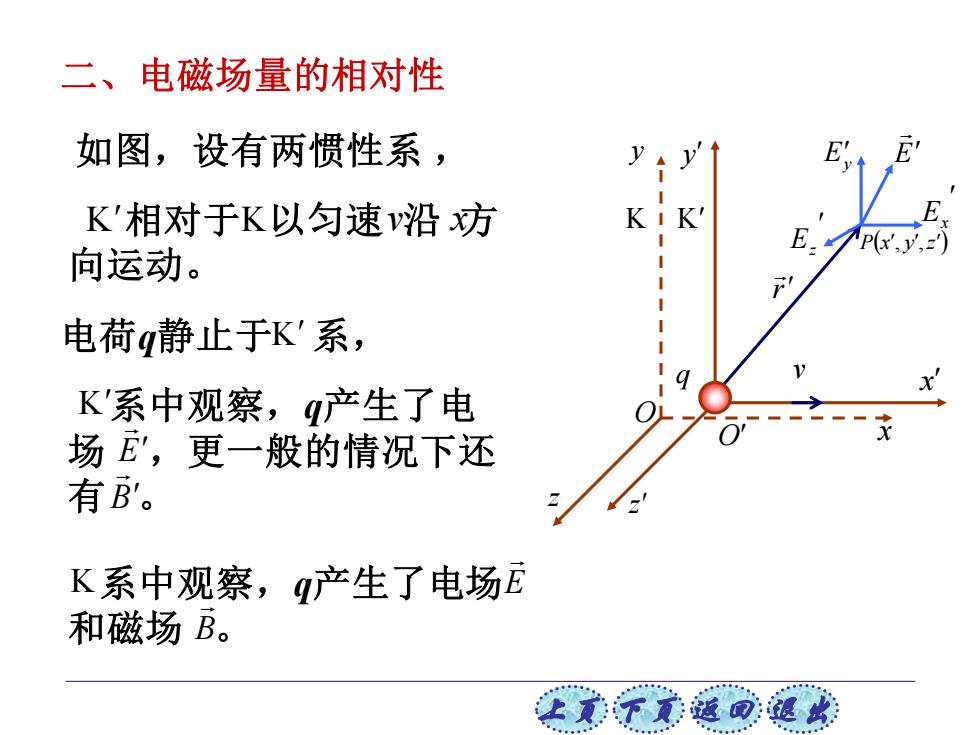
上页 下页 返回 退出 二、电磁场量的相对性 K K y y z z O q O v x x r E z Ey E Ex P(x , y ,z ) 如图,设有两惯性系 , 相对于 以匀速 沿 方 向运动。 K K v x 电荷q静止于 K 系, 系中观察,q产生了电场 和磁场 。 K E B 系中观察,q产生了电 场 ,更一般的情况下还 有 。 K E B

按洛伦兹变换可以证明,在不同的惯性参考系中 电磁场各场量的关系是 E.=E.E,=1E +vB.E.=E.-vB 其中 2 上式中速度V变为一V即得逆变换 让美觉返司退
上页 下页 返回 退出 按洛伦兹变换可以证明,在不同的惯性参考系中 电磁场各场量的关系是 + = − = = − = + = = 2 2 , , , , c v E B B c v E B B B B E E E E v B E E v B y z z z x x y y x x y y x z z y 其中 2 2 1 1 c v − = 上式中速度 v 变为 −v 即得逆变换
在不同惯性系中采用各自的时间、空间、场量 来描述电磁现象,即描述电磁现象的量在不同惯性 系内有不同的量值,说明电磁场量是相对的;但每 一惯性系中电磁场量之间的关系都有相同的麦克斯 韦方程组形式,说明电磁规律是绝对的。 电磁场量变换关系的应用 y 图示电荷静止于K'系原点 KIK' 某时刻测得某点处的电磁场为 P(x,y,z' E= 写成分量形式 让贰下觉返回退此
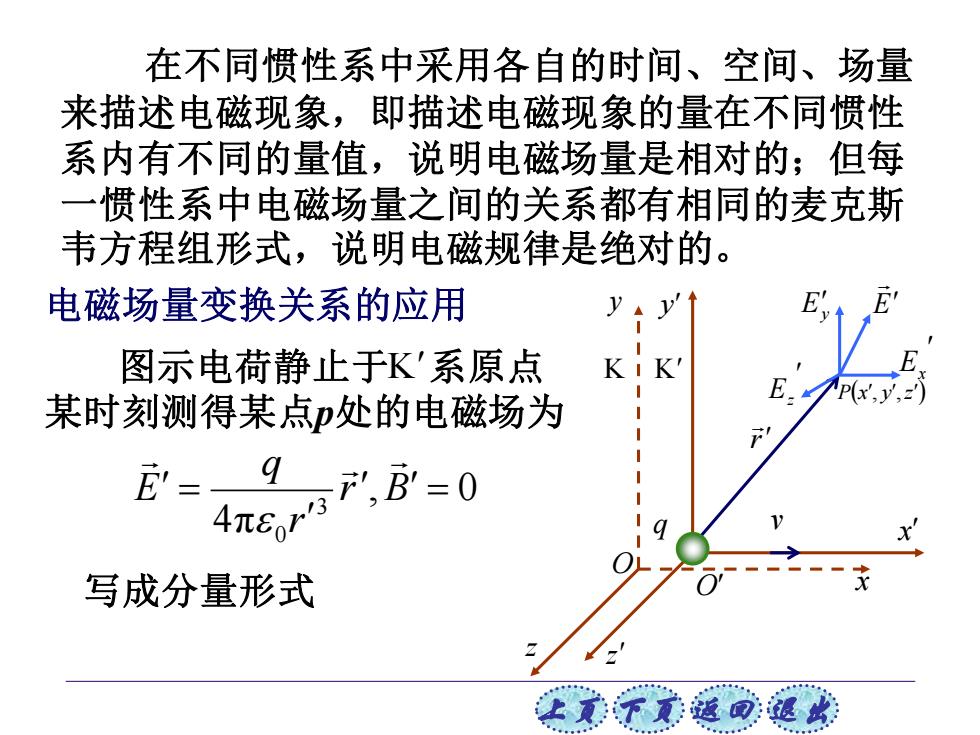
上页 下页 返回 退出 在不同惯性系中采用各自的时间、空间、场量 来描述电磁现象,即描述电磁现象的量在不同惯性 系内有不同的量值,说明电磁场量是相对的;但每 一惯性系中电磁场量之间的关系都有相同的麦克斯 韦方程组形式,说明电磁规律是绝对的。 电磁场量变换关系的应用 K K y y z z O q O v x x r E z Ey E Ex 图示电荷静止于 系原点 P(x , y ,z ) 某时刻测得某点p处的电磁场为 K , 0 4π 3 0 = = r B r q E 写成分量形式
gx" = 4π8r B=0 qv' ,=4E5 =0 (1) E.= 92' 4πr8 B:=0 其电场线以点电荷为中 心,向各个方向均匀分 布。图示为在K'系中电 场线的分布。K系内观 察除电场外还有磁场。 点电荷静止或低速下的电场线分布 王觉不元菠面:退收
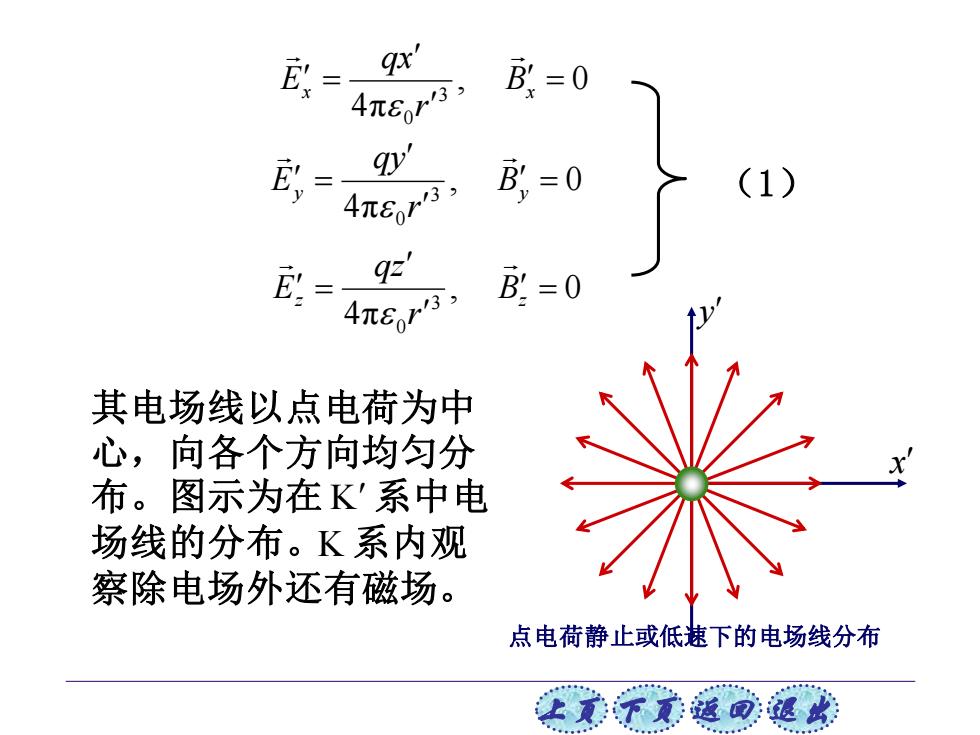
上页 下页 返回 退出 , 0 4π 3 0 = x = Bx r qx E , 0 4π 3 0 = y = By r qy E , 0 4π 3 0 = z = Bz r qz E 其电场线以点电荷为中 心,向各个方向均匀分 布。图示为在 系中电 场线的分布。 系内观 察除电场外还有磁场。 K K (1) y x 点电荷静止或低速下的电场线分布

在K系内观察,点电荷以速度下沿x轴方向运动, 除电场外还观察到磁场。由上述场量的变换关系,可得 时刻在P(x,y,z点处的电磁场为 E,=Ex,Ey=yEy,E:=yE: (2) B=0B,=-yg,=y x'=y(x-vt),y'=y,z'=2, 又 r'=vx2+y2+=2=vr(x-vt+y2+=2 将方程组(1)、(3)代入(2)得
上页 下页 返回 退出 2 2 0 , , , c v E B c v E B B E E E E E E y z z x y x x y y z z = = = − = = = 又 ( ) ( ) 2 2 2 2 2 2 , , , r x y z x v t y z x x v t y y z z = + + = − + + = − = = 在 系内观察,点电荷 以速度 沿 轴方向运动, 除电场外还观察到磁场。由上述场量的变换关系,可得 时刻在 点处的电磁场为 K q v x t P(x, y,z) (2) (3) 将方程组(1) 、(3) 代入(2)得

Ex= ng(x-vt) 4π26-}+y2+z2 B.=0 rqy E,4(-时+y+可 B =- E:( (4) E. Yqz 4e6-+y+丽 B.= 由上式可见,在K系内电场分布已不再是球对称,平 行于电荷运动方向的场强量小于电荷静止时的场强, 而垂直于场强方向的平面内的场强分量则大于电荷静 止时的场强(见下图)。 让美下觉返同速
上页 下页 返回 退出 ( ) ( ) ( ) ( ) z z y y y z x x E c v B x v t y z qz E E c v B x v t y z qy E B x v t y z q x v t E 3/ 2 2 2 2 2 2 0 3/ 2 2 2 2 2 2 0 3/ 2 2 2 2 2 0 , 4π , 4π , 0 4π = − + + = = − − + + = = − + + − = 由上式可见,在K系内电场分布已不再是球对称,平 行于电荷运动方向的场强量小于电荷静止时的场强, 而垂直于场强方向的平面内的场强分量则大于电荷静 止时的场强(见下图)。 (4)

磁场的空间分布情况,磁 点电 感应线分布在垂直于运动方向 荷高 的平面内,是以电荷运动方向 速下 的电 为中心线的同心圆。磁感应线 场线 分布 方向和正电荷的运动方向仍服 从右手螺旋定则。 洛伦兹变换和上面的例 子说明不同惯性系中电场和 磁场的相对性和电场和磁场 的不可分割性。 电荷在K系内的场强
上页 下页 返回 退出 磁场的空间分布情况,磁 感应线分布在垂直于运动方向 的平面内,是以电荷运动方向 为中心线的同心圆。磁感应线 方向和正电荷的运动方向仍服 从右手螺旋定则。 洛伦兹变换和上面的例 子说明不同惯性系中电场和 磁场的相对性和电场和磁场 的不可分割性。 y x 点电 荷高 速下 的电 场线 分布 v x y z r r E(x, y,z) B o q 电荷在K系内的场强

Ex=E,Ey=yEy E:=E B=0,B=-yEg,=7 2 vE ,B= 合写成矢量式 c2 ×E B= B= vEsin 0 c 、2 (4) B+E+E=AnSo r sin20 据前述 方程组 让文下觉返司退此
上页 下页 返回 退出 2 2 0, , , , c v E B c v E B B E E E E E E y z z x y x x y y z z = = = − = = = 0 2 2 , , c v E B c v E B B y z z x= y = − = 2 c v E B = 合写成矢量式 2 sin c v E B = 据前述 方程组 (4) 3 2 2 2 2 2 0 2 2 2 1 sin 1 4π 1 − − = + + = c v c v r q E Ex Ey Ez

sin 0 B=Ho qv 4πr2 3/2 - sin20 当运动电荷的速度很小时(v<c),略去前式中的(v/c) 项,则在K系中观测的场强为 i=_ g r (1) 4π80r1 B=×E=么x (2) 4π r3 即当运动电荷的速度很小时,它所激发的电磁 场就接近于恒定流动情况所激发的电磁场。 王元不元返可退华
上页 下页 返回 退出 3 2 2 2 2 2 0 1 sin 1 sin 4π − − = c v c v r qv B (2) 4π (1) 4π 3 0 2 3 0 r qv r E c v B r q r E = = = 当运动电荷的速度很小时 ,略去前式中的 项,则在 系中观测的场强为: (v c) ( ) 2 v / c K 即当运动电荷的速度很小时,它所激发的电磁 场就接近于恒定流动情况所激发的电磁场