
§,7-7.电容器的电容 一、 孤立导体的电容 真空中孤立导体球 R V= 19 4π80R =4元8R V 任何孤立导体,q/V与q、均无关,定义为孤立导 体的电容。 电容单位:F(法拉) 1F=106uF=109nF=1012pF 电容是表征导体储电能力的物理量,其物理意义是 使导体升高单位电势所需的电荷量。 让文不美蕴回蕴以
上页 下页 返回 退出 §7-7 电容器的电容 一、孤立导体的电容 真空中孤立导体球 R R q V 4π 0 1 = 任何孤立导体,q/V与q、V均无关,定义为孤立导 体的电容。 R V q 4π 0 = V q C = 电容单位: F(法拉) 1F 10 μF 10 nF 10 pF 6 9 12 = = = 电容是表征导体储电能力的物理量,其物理意义是 使导体升高单位电势所需的电荷量

二、 电容器的电容 电容器:两相互绝缘的导体组成的系统。 电容器的两极板常带等量异号电荷。 几种常见电容器及其符号: 让贰子元道同退此
上页 下页 返回 退出 二、 电容器的电容 电容器:两相互绝缘的导体组成的系统。 电容器的两极板常带等量异号电荷。 几种常见电容器及其符号:
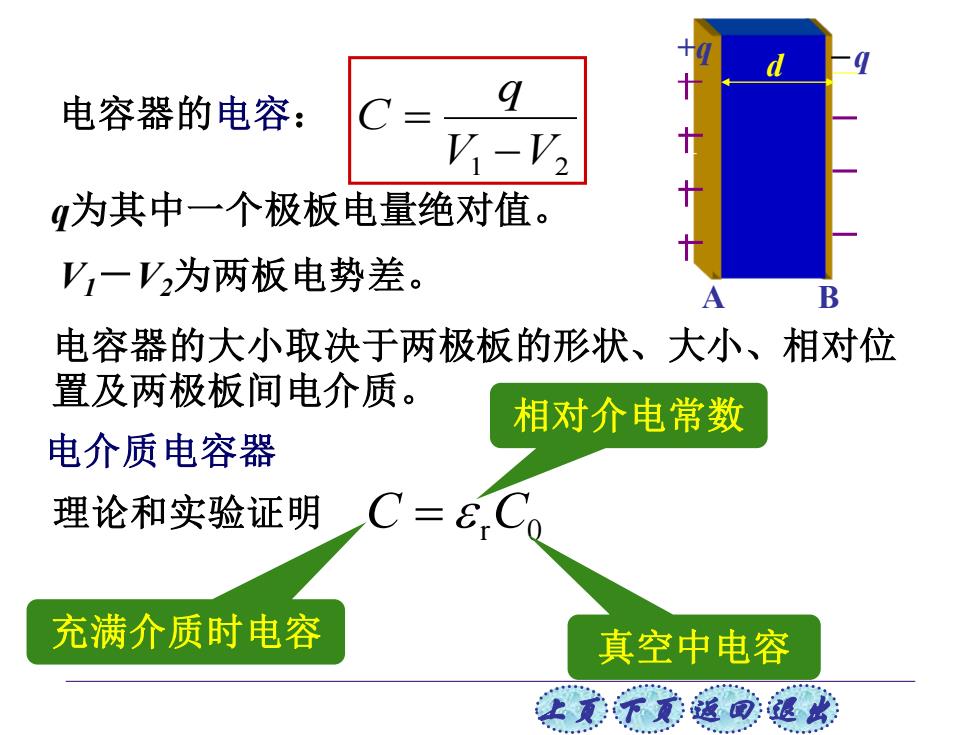
电容器的电容: V-V2 为其中一个极板电量绝对值。 V,一V,为两板电势差。 A B 电容器的大小取决于两极板的形状、大小、相对位 置及两极板间电介质。 相对介电常数 电介质电容器 理论和实验证明 C=8( 充满介质时电容 真空中电容 让美不觉返司退
上页 下页 返回 退出 V1 V2 q C − = q为其中一个极板电量绝对值。 V1-V2为两板电势差。 电容器的电容: 电容器的大小取决于两极板的形状、大小、相对位 置及两极板间电介质。 A B d +q -q 电介质电容器 理论和实验证明 C r C0 = 充满介质时电容 相对介电常数 真空中电容

计算电容的一般方法: 先假设电容器的两极板带等量异号电荷,再计算 出电势差,最后代入定义式。 几种常见真空电容器及其电容 例题7-23平板电容器 因为 E=0 Eo 所以 U.-U.=[E-di=d oS 所以 Co=U.-U. od 8o d 电容与极板面积成正比,与间距成反比。 让贰下觉返回退
上页 下页 返回 退出 例题7-23 平板电容器 几种常见真空电容器及其电容 S + 0 − E = − + + − U −U = E l d d 0 = d + − − = U U q C0 d S d S 0 0 / = = 电容与极板面积成正比,与间距成反比。 计算电容的一般方法: 先假设电容器的两极板带等量异号电荷,再计算 出电势差,最后代入定义式。 因为 所以 所以
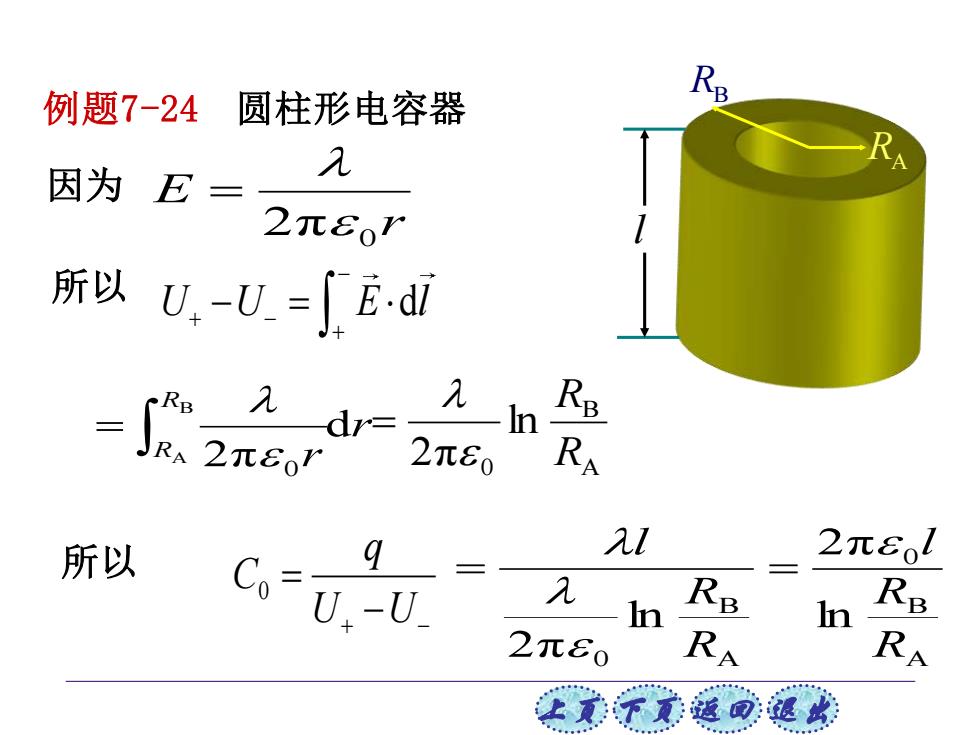
例题7-24 圆柱形电容器 Q 因为E= 几 2元80r 所以U,-U.=E.dl Re 2元80 几l 所以 2元8o1 U.-U. 兄 Re In Re 2元80 RA RA 让美觉返司退此
上页 下页 返回 退出 例题7-24 圆柱形电容器 r E 2π 0 = U U E l d − + − + − = r r R R d 2π B A 0 = + − − = U U q C0 A B 0 A B 0 ln 2π ln 2π R R l R R l = = A B 0 ln 2π R R = RB RA l 因为 所以 所以
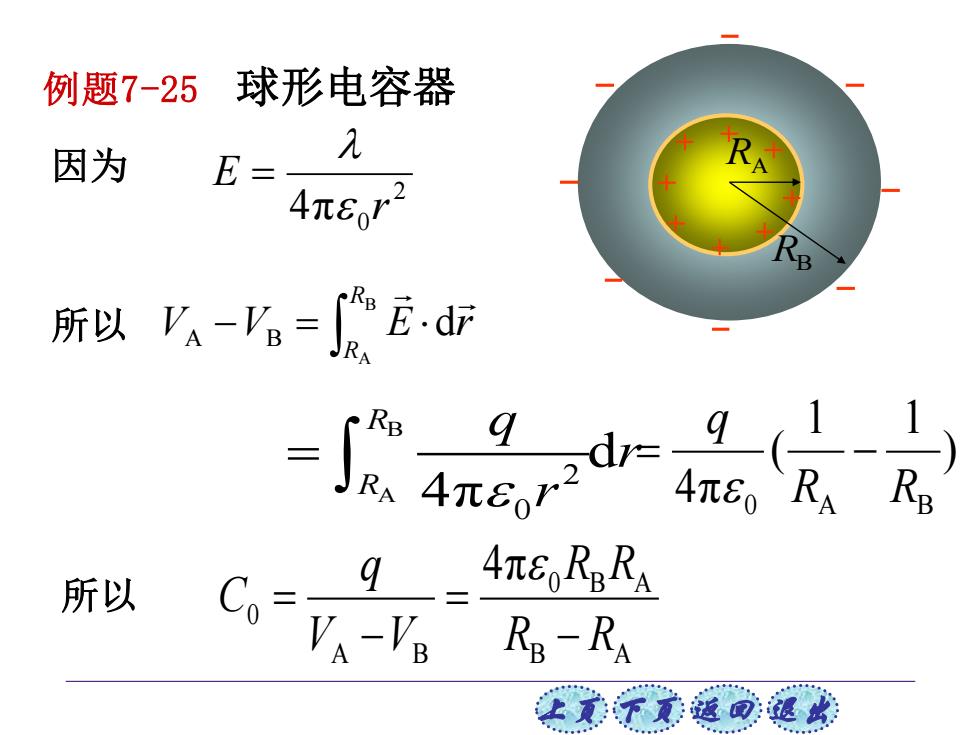
例题7-25 球形电容器 因为 几 E= 4π82 B 所以-。=心万.d C RB 所以 Co= 9_4πGRRA A-'gR常-RA 上美不元返回退
上页 下页 返回 退出 例题7-25 球形电容器 B A 0 B A A B 0 4π R R R R V V q C − = − = B A 2 0 d 4π R R q r r = ) 1 1 ( 4π 0 RA RB q = − RA RB 2 4π 0 r E 因为 = − = B A A B d R R V V E r 所以 所以

电容器两极板间如果充满某种相对电容率为8,的电介 质,则上面三种电容器的电容分别为 平行板电容器:C ErE0S d 圆柱形电容器: C 2π8,80l n Re RA 球形电容器: RARB C=4πE,B0RB-RA 电容器的重要性能指标:电容、耐压值。 让美下元返回:退欢
上页 下页 返回 退出 电容器两极板间如果充满某种相对电容率为 的电介 质,则上面三种电容器的电容分别为 r 平行板电容器: 圆柱形电容器: 球形电容器: d S C r 0 = A B r 0 ln 2π R R l C = B A A B 4π r 0 R R R R C − = 电容器的重要性能指标:电容、耐压值

三、电容器的串联和并联 1.串联: C 2 C. 所以 串联等效电容器的电容倒数等于每个电容器电容倒 数之和。电容器串联后总的耐压值为每个的耐压值 之和,提高了耐压
上页 下页 返回 退出 三、电容器的串联和并联 1.串联: . C1 C2 CN +q -q +q -q +q -q U Q C = = i Ui q = i Ci q q C C C CN 1 1 1 1 1 2 所以 = + ++ 串联等效电容器的电容倒数等于每个电容器电容倒 数之和。电容器串联后总的耐压值为每个的耐压值 之和,提高了耐压
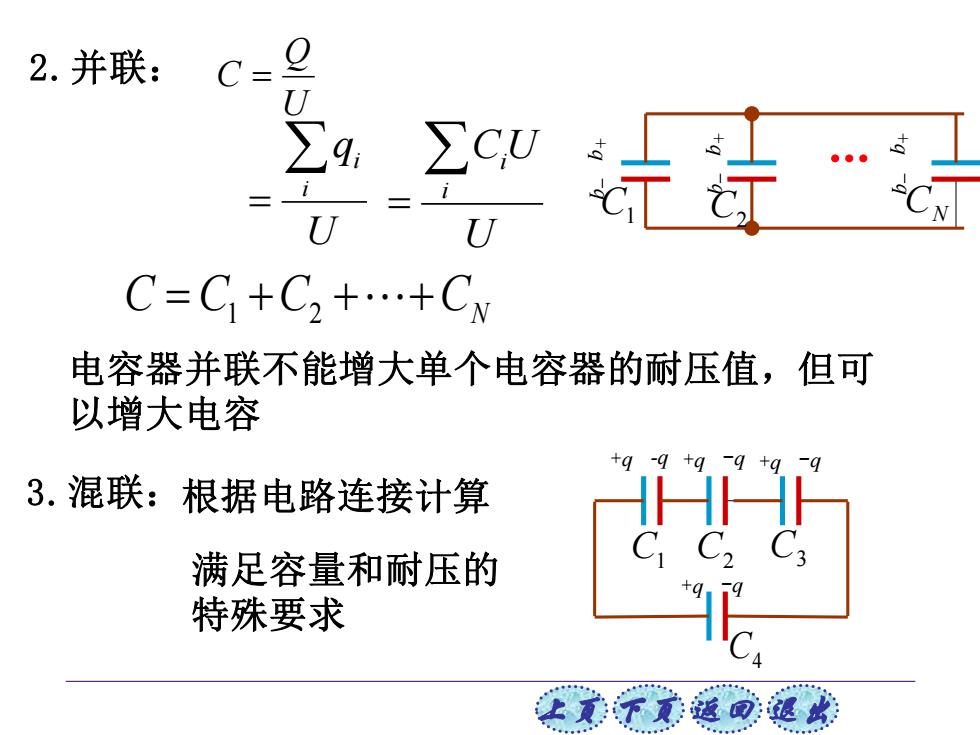
2.并联: C= C=C+C2++C 电容器并联不能增大单个电容器的耐压值,但可 以增大电容 3.混联:根据电路连接计算 满足容量和耐压的 特殊要求 让美不觉返同速
上页 下页 返回 退出 3.混联:根据电路连接计算 满足容量和耐压的 特殊要求 2.并联: C = C1 +C2 ++CN 电容器并联不能增大单个电容器的耐压值,但可 以增大电容 . C1 C2 CN + q - q + q - q + q - q C1 C2 C3 C4 +q -q +q -q +q -q +q -q U Q C = U q i i = U CU i i =
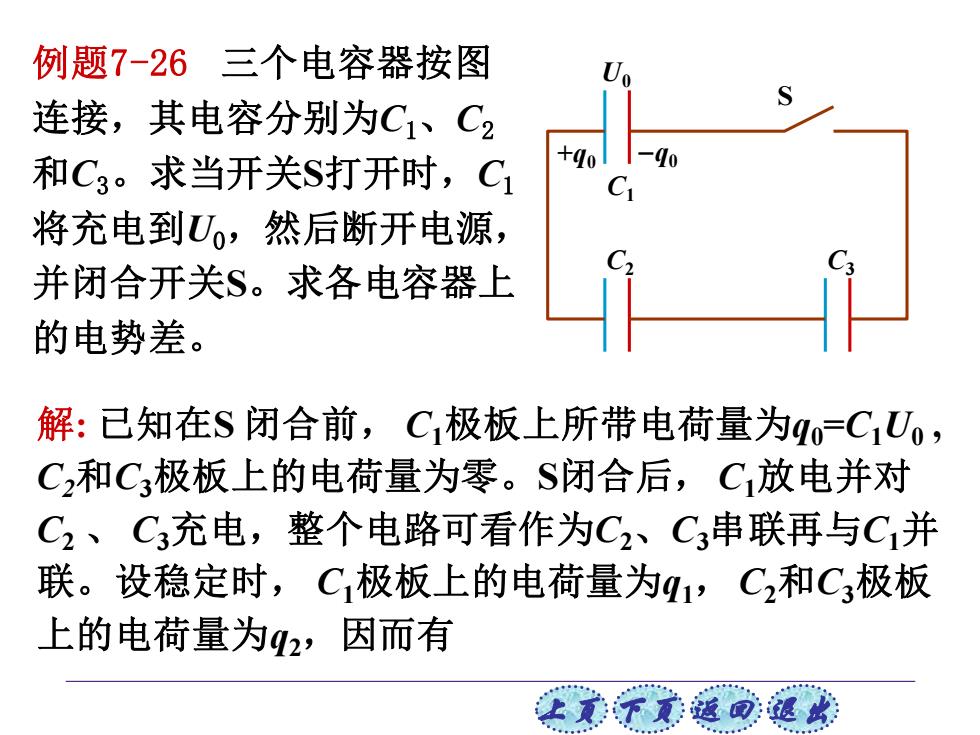
例题7-26三个电容器按图 连接,其电容分别为C1、C2 和C3。求当开关S打开时,C1 -0 将充电到Uo,然后断开电源, 并闭合开关S。求各电容器上 的电势差。 解:已知在S闭合前,C1极板上所带电荷量为q0=C1U, C,和C3极板上的电荷量为零。S闭合后,C放电并对 C2、C3充电,整个电路可看作为C2、C串联再与C1并 联。设稳定时,C1极板上的电荷量为q1,C2和C3极板 上的电荷量为q2,因而有
上页 下页 返回 退出 例题7-26 三个电容器按图 连接,其电容分别为C1、C2 和C3。求当开关S打开时,C1 将充电到U0,然后断开电源, 并闭合开关S。求各电容器上 的电势差。 解: 已知在S 闭合前, C1极板上所带电荷量为q0=C1U0 , C2和C3极板上的电荷量为零。S闭合后, C1放电并对 C2 、 C3充电,整个电路可看作为C2、C3串联再与C1并 联。设稳定时, C1极板上的电荷量为q1, C2和C3极板 上的电荷量为q2,因而有 S U0 +q0 −q0 C1 C2 C3