§7-2i 静电场 电场强度 一、 电场 作用 超距作用 电荷1 电荷2 作用 两种观点 产生电场1作用 电场 电荷1 电荷2 作用电场2江生 电场力:电场对处于其中的其他电荷的作用力,电荷 间的相互作用力本质上是各自的电场作用于对方的电 场力。 静电场:相对于观察者静止的电荷在周围空间激发的 电场。 让美下觉返司速此
上页 下页 返回 退出 §7-2 静电场 电场强度 一、 电场 两种观点{ 超距作用 作用 作用 电场 电荷1 电荷2 电场1 电场2 电荷1 电荷2 静电场:相对于观察者静止的电荷在周围空间激发的 电场。 电场力:电场对处于其中的其他电荷的作用力,电荷 间的相互作用力本质上是各自的电场作用于对方的电 场力
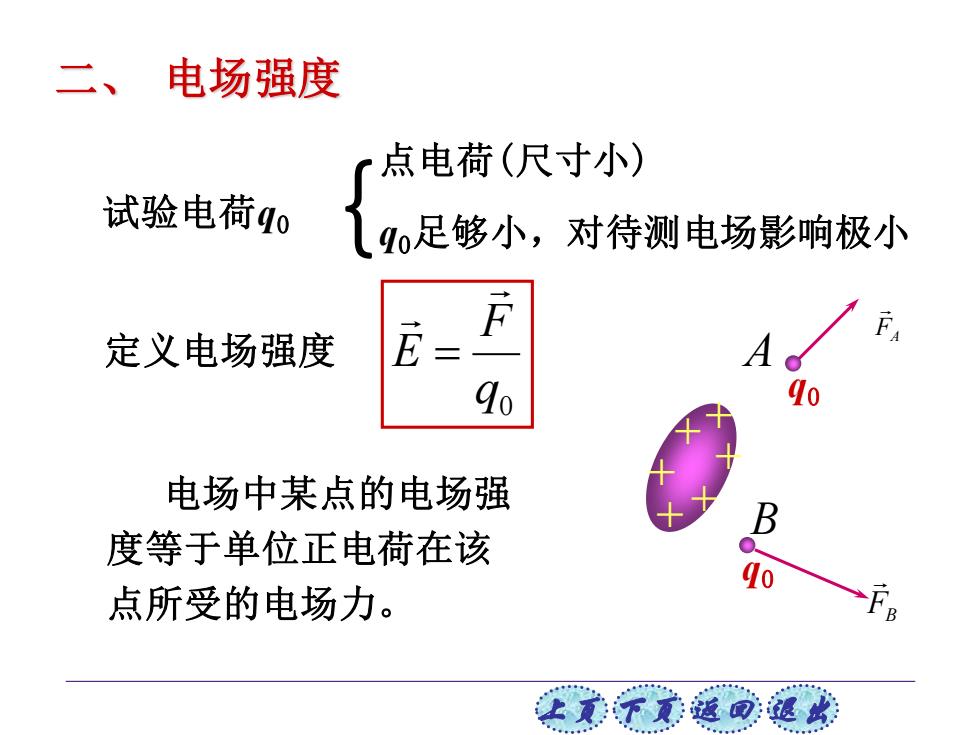
二、 电场强度 点电荷(尺寸小) 试验电荷qo qo足够小,对待测电场影响极小 定义电场强度 A 90 0 电场中某点的电场强 B 度等于单位正电荷在该 90 点所受的电场力。 B 上意订意返回退
上页 下页 返回 退出 二、 电场强度 试验电荷q0 { 点电荷(尺寸小) q0足够小,对待测电场影响极小 定义电场强度 + + + + + + q0 FB B 电场中某点的电场强 度等于单位正电荷在该 点所受的电场力。 q0 F E = A FA q0
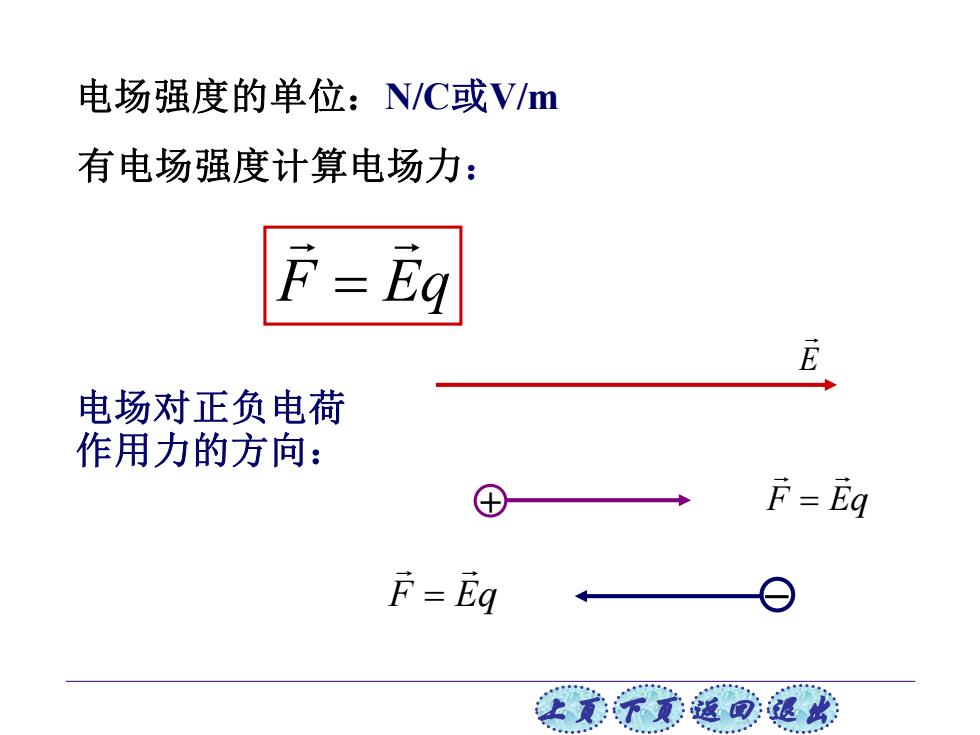
电场强度的单位:N/C或Vm 有电场强度计算电场力: F=Eq 电场对正负电荷 作用力的方向: F=Eq F=Eq 让意文滋可退攻
上页 下页 返回 退出 电场强度的单位:N/C或V/m 有电场强度计算电场力: F Eq = E 电场对正负电荷 作用力的方向: + F Eq = F Eq =

例题7-3试求电偶极子在均匀外电场中所受的作, 并分析电偶极子在非均匀外电场中的运动。 电偶极子定义:一对相距为1带电量相同,电性相反的 点电荷系。 电偶极子的电偶极矩:p=ql,1为由负电荷指向正电荷 解:如图所示,在均匀外电场 中,电偶极子的正负电荷上的 电场力的大小为 F=F=F=gE 大小相等、方向相反,合力为零; 由于五和 产生的合力矩大小为 让意不意通可退欢
上页 下页 返回 退出 例题7-3 试求电偶极子在均匀外电场中所受的作, 并分析电偶极子在非均匀外电场中的运动。 p +q E F1 F2 − q M 解:如图所示,在均匀外电场 中,电偶极子的正负电荷上的 电场力的大小为 F = F1 = F2 = qE 由于 F1 和 F1 大小相等、方向相反,合力为零; 产生的合力矩大小为 电偶极子定义:一对相距为l 带电量相同,电性相反的 点电荷系。 电偶极子的电偶极矩: p ql , = l 为由负电荷指向正电荷

M=FIsin=qElsin0=pEsin0矢量式为M=pxE 在此力矩作用下电偶极矩将转向外电场方向直到电矩 与外电场方向一致。 在非均匀外电场中,电偶极子一方面受力矩作用,另 一方面,所受合力不为零,场强较强一端电荷受力较 大,促使偶极子向场强较强方向移动,如图所示: 让美觉返司退
上页 下页 返回 退出 M p E M = Flsin = qElsin = pEsin 矢量式为 = 在此力矩作用下电偶极矩将转向外电场方向直到电矩 与外电场方向一致。 在非均匀外电场中,电偶极子一方面受力矩作用,另 一方面,所受合力不为零,场强较强一端电荷受力较 大,促使偶极子向场强较强方向移动,如图所示: F1 F2 − q F1 +q F2 +q − q F2 − q +q F1

三、电场强度的计算 1.点电荷的电场 疗= 1 9o9 4元B0 7.2 e 龙 京 场点 e 90 E 源点 让贰下觉返回退
上页 下页 返回 退出 场点 源点 1. 点电荷的电场 q 0 2 0 1 4π r q q F e r = E = q0 F 2 0 1 4π r q e r = F E + E r E r r 0 q 三、电场强度的计算
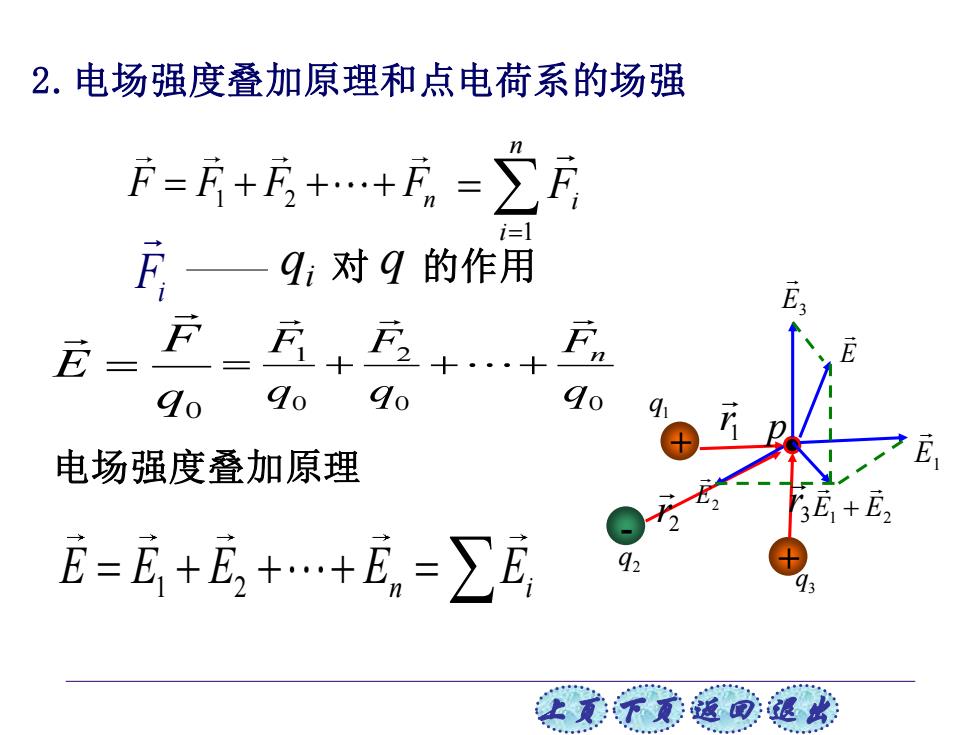
2.电场强度叠加原理和点电荷系的场强 F=耳+月++E=∑F F—9:对9的作用 E 龙= F go go 90 9o 电场强度叠加原理 E=E+E+.+E。=∑E 让美下觉返司速此
上页 下页 返回 退出 2.电场强度叠加原理和点电荷系的场强 F F F F = + + + 1 2 n q q i 对 的作用 Fi q0 F E = 0 0 2 0 1 q F q F q F n = + + + E E E E E 1 2 n i = + + + = = = n i Fi 1 电场强度叠加原理 + + - E3 E1 E1 E2 + E E2 r1 p 2 r 3 r 3 q 2 q 1 q

点电荷系的电场 E,= 4π80r1 E=E,+E2++E 8- 1 2 4元80 91 可见,点电荷系在空间任一点所激发的总场强 等于各个点电荷单独存在时在该点各自所激发的场 强的矢量和。 上美不意道可退欢
上页 下页 返回 退出 点电荷系的电场 E E E En = 1 + 2 + + = = n i ri i i e r q E 1 2 4π 0 1 q2 qn q1 qi P rn r2 r1 ri 可见,点电荷系在空间任一点所激发的总场强 等于各个点电荷单独存在时在该点各自所激发的场 强的矢量和。 1 q n q 2 q i q p n r 2 r 1 r i r ri i i i e r q E 2 4π 0 1 =
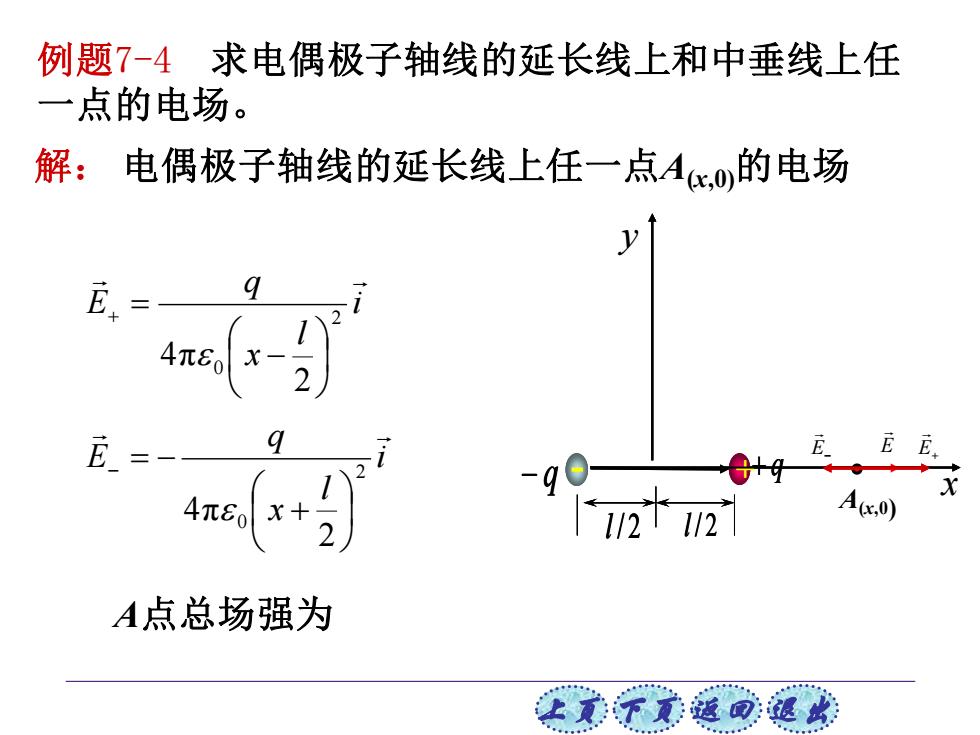
例题7-4求电偶极子轴线的延长线上和中垂线上任 一点的电场。 解:电偶极子轴线的延长线上任一点Ax,0的电场 480 x- EEE 4e刘x+2 9 112T12 Aix.) A点总场强为 让美觉返司退
上页 下页 返回 退出 y x A(x,0) E− E E+ + + q − q l / 2 l / 2 例题7-4 求电偶极子轴线的延长线上和中垂线上任 一点的电场。 解: 电偶极子轴线的延长线上任一点A(x,0)的电场 + + q − q l / 2 l / 2 i l x q E 2 0 2 4π − + = i l x q E 2 0 2 4π + − = − A点总场强为 + q − q l / 2 l / 2

E=E.+E 1-1- 因为x>>l =i-a2 让意了贰道回退此
上页 下页 返回 退出 EA = E+ + E− 2 2 0 1 1 4 2 2 q i l l x x = − − + i x l x l x qxl 2 2 0 2 1 2 4π 1 2 + − = i x ql EA 3 0 2 4π 1 = i x p 3 0 2 4π 1 = 因为x>>l