
§5-3理想气体的压强和温度公式 一、 理想气体的微观模型 力学假设 (1)气体分子当作质点,不占体积,体现气态的特性; (2)气体分子的运动遵从牛顿力学的规律; (3)分子之间除碰撞的瞬间外,无相互作用力,碰撞为 弹性碰撞;一般情况下,忽略重力。 统计假设: (1)分子的速度各不相同,而且通过碰撞不断变化着; (2) 平衡态时分子按位置的分布是均匀的,即分子数密 度到处一样,不受重力影响; (3)平衡态时分子的速度按方向的分布是各向均匀的。 ===v213 王觉下元菠面:退此
上页 下页 返回 退出 力学假设 (1)气体分子当作质点,不占体积,体现气态的特性; (2)气体分子的运动遵从牛顿力学的规律; (3)分子之间除碰撞的瞬间外,无相互作用力,碰撞为 弹性碰撞;一般情况下,忽略重力。 一、理想气体的微观模型 统计假设: (3)平衡态时分子的速度按方向的分布是各向均匀的。 (1)分子的速度各不相同,而且通过碰撞不断变化着; (2)平衡态时分子按位置的分布是均匀的,即分子数密 度到处一样,不受重力影响; 2222 / 3 x y z vvvv === §5-3 理想气体的压强和温度公式
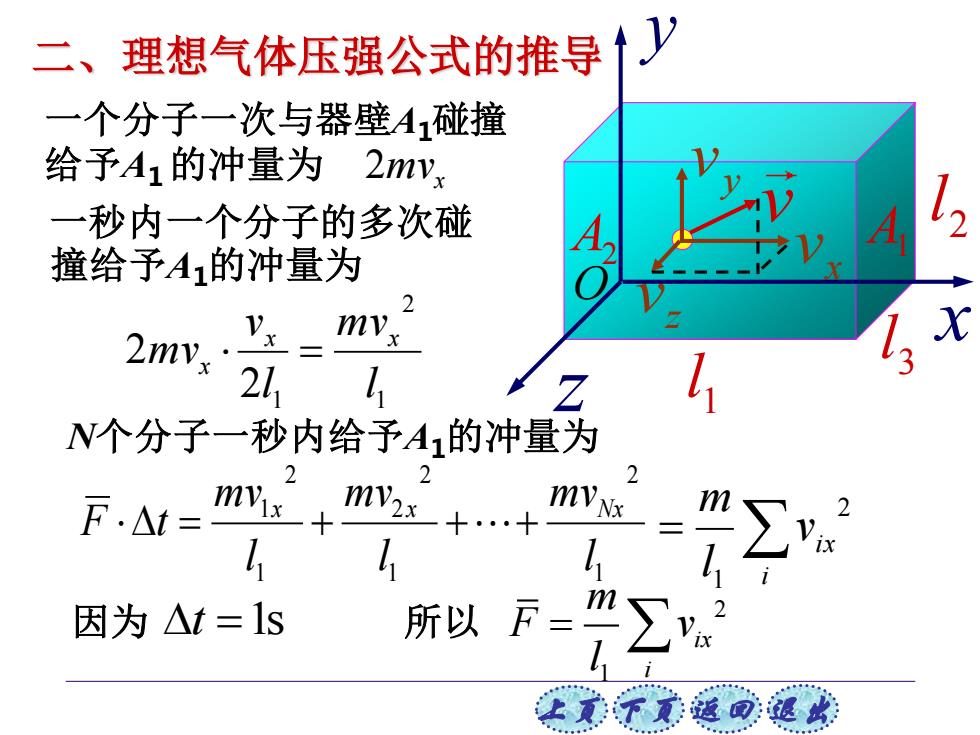
二、 理想气体压强公式的推导↑y 一个分子一次与器壁A1碰撞 给予A1的冲量为2mv 一秒内一个分子的多次碰 撞给予A1的冲量为 2mvx mv 21 N个分子一秒内给予A的冲量为 2 F.△t= mv2x 因为△t=ls 所以F=
上页 下页 返回 退出 1 l 2 l 3 l A2 A1 一秒内一个分子的多次碰 撞给予A1的冲量为 1 2 1 2 2 l mv l v mv x x x = 二、理想气体压强公式的推导 v x v y v z v 一个分子一次与器壁A1碰撞 给予A1 的冲量为 mvx 2 N个分子一秒内给予A1的冲量为 1 2 1 2 2 1 2 1 l m v l m v l m v F t x x Nx = + ++ = i ix v l m 2 1 =t 1s 2 1 ix i m F v l = y x z O 因为 所以

A1上的压强 F p= v.2 Nm.2+22++2 113 N =nm·V 因 2=2= 故 p 定义分子的平均平动动能为 -mv 压强 则 nEx 公式 王觉下元菠面:退收
上页 下页 返回 退出 A1上的压强 2 3 l l F p = N v v v V Nm x x Nx 2 2 2 2 1 + + + = 2 x = nmv = i i x v l l l m 2 1 2 3 2 2 2 x y z v v v = = 2 3 1 = v 1 2 3 p nmv = 定义分子的平均平动动能为 2 k 1 2 = mv 则 = 2 2 1 3 2 p n mv k 2 3 p n = 压强 公式 因 故

讨论: pocn p ock (1)对容器其他面的推算结果相同; (2)对一般形状的容器可证有相同结果; (3)这是一个统计结果,只有对大量的分子才有意义。 三、温度的本质和统计意义 根据理想气体的压强公式和状态方程可导出 宏观量温度T与有关微观量的关系,从而揭示温 度的微观实质。 质量为m的理想气体,分子数为N,分子 质量为m,则有:m=Nm 1mol气体的分子数为N,则有Mn=Nm 上意不意返回:退
上页 下页 返回 退出 (1)对容器其他面的推算结果相同; (2)对一般形状的容器可证有相同结果; (3)这是一个统计结果,只有对大量的分子才有意义。 p n k p 三、温度的本质和统计意义 根据理想气体的压强公式和状态方程可导出 宏观量温度 T 与有关微观量的关系,从而揭示温 度的微观实质。 质量为 m 的理想气体,分子数为 N ,分子 质量为 m0 ,则有: m Nm = 0 1 mol 气体的分子数为N0 ,则有 M N m mol 0 0 = 讨论:
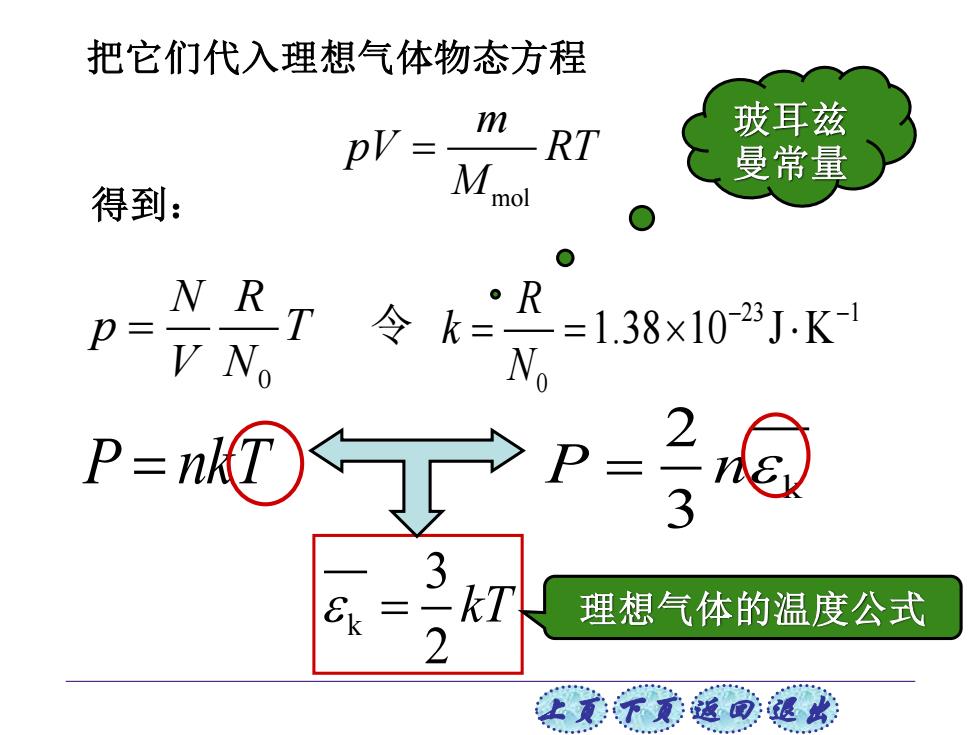
把它们代入理想气体物态方程 pV= m 玻耳兹 RT M mol 曼常量 得到: 卫= 令k= V No =1.38x1025J-K No P=n①> P= 2@ 3 kT 理想气体的温度公式 2 让美下觉返司速此
上页 下页 返回 退出 23 1 0 1.38 10 J K R k N − − = = P = nkT k 2 3 P n = k 3 2 = kT 0 N R p T V N = 令 把它们代入理想气体物态方程 理想气体的温度公式 mol m pV RT M = 得到: 玻耳兹 曼常量

温度的统计意义 a.温度实质(统计概念) 统计平均值 3 6=T 宏观量温度 微观量平均平动动能 2 反映大量分子 热运动剧烈程度 b.温度反映大量分子热运动的剧烈程度。 上美不意通可退
上页 下页 返回 退出 温度的统计意义 k 3 2 = kT 宏观量温度 微观量平均平动动能 统计平均值 a. 温度实质(统计概念) b. 温度反映大量分子热运动的剧烈程度。 热运动剧烈程度

四、气体分子的方均根速率 -1 Ek=mv= 2 2 大量分子速率的平方平均值的平方根 voT 3kT 3RT m Fx1l、Ma 气体分子的方均根速率与气体的热力学温度的平 方根成正比,与气体的摩尔质量的平方根成反比。 王文下美菠面:退收
上页 下页 返回 退出 四、气体分子的方均根速率 2 v 大量分子速率的平方平均值的平方根 2 0 mol 3 3 kT RT v m M = = 2 k 1 3 2 2 = = mv kT 气体分子的方均根速率与气体的热力学温度的平 方根成正比,与气体的摩尔质量的平方根成反比。 v T 2 2 mol v M 1 /

例题5-3一容器内贮有气体,温度27℃。问(1)压 强为1.013×105Pa时,在1m3中有多少个分子; (2)在高真空时,压强为1.33×105Pa,在1m3中有 多少个分子? 解:由p=nkT可得到单位体积内的分子数为 (1) n= =2.45×1025m3 kT (2) n= =3.21x105m3 kT 上意不家返可退此
上页 下页 返回 退出 (1) (2) 25 3 2.45 10 m p n kT − = = 15 3 3.21 10 m p n kT − = = 例题5-3 一容器内贮有气体,温度27℃。问(1)压 强为 1.013×105Pa时,在1m3中有多少个分子; (2)在高真空时,压强为1.33×10-5Pa,在1m3中有 多少个分子? 解:由p=nkT可得到单位体积内的分子数为

例题5-4试求氮气分子的平均平动动能和方均根速 率,设(1)在温度仁100°℃时,(2)在温度仁0°℃ 时,(3)在温度仁-150°C时? 解:(1)在温度仁100C时 。3 6k=。kT=7.71×10-21J 2 3RT =5.74×10m/s (2)同理在温度t=0°C时 3 Ek= kT=5.65×10-21J 2 让美下觉返司速此
上页 下页 返回 退出 例题5-4 试求氮气分子的平均平动动能和方均根速 率,设(1)在温度 t=100°C 时,(2)在温度 t=0 °C 时,(3)在温度t=-150°C 时? 2 2 mol 3 5.74 10 m/s RT v M = = 21 k 3 7.71 10 J 2 kT − = = (2)同理在温度t=0°C 时 21 k 3 5.65 10 J 2 kT − = = 解:(1)在温度 t=100°C 时

3RT =493m/s (3)在温度-150°C时 a-27=255×102叮町 2 3RT =331m/s 让美不家返可退此
上页 下页 返回 退出 (3)在温度t=-150°C时 2 mol 3 331m/s RT v M = = 21 k 3 2.55 10 J 2 kT − = = 2 mol 3 493m/s RT v M = =