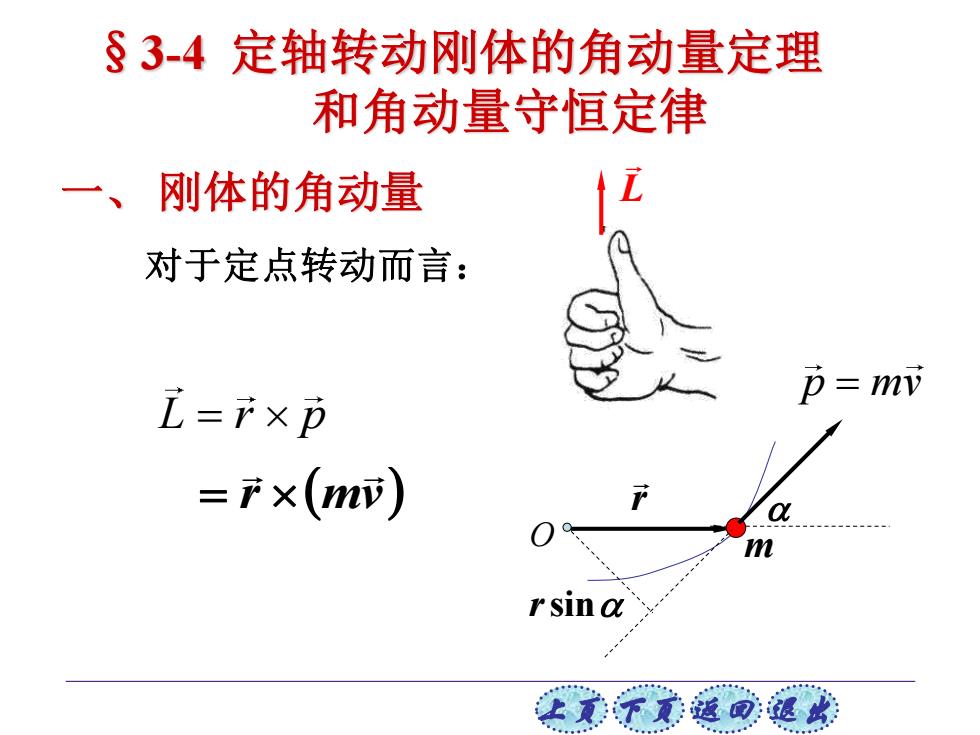
§3-4定轴转动刚体的角动量定理 和角动量守恒定律 一、 刚体的角动量 对于定点转动而言: 瓦=F×p p=mv =产×(m) rsina 上贰不觉返退此
上页 下页 返回 退出 一、 刚体的角动量 对于定点转动而言: L L r p = r m p mv = rsin O r (mv ) = §3-4 定轴转动刚体的角动量定理 和角动量守恒定律
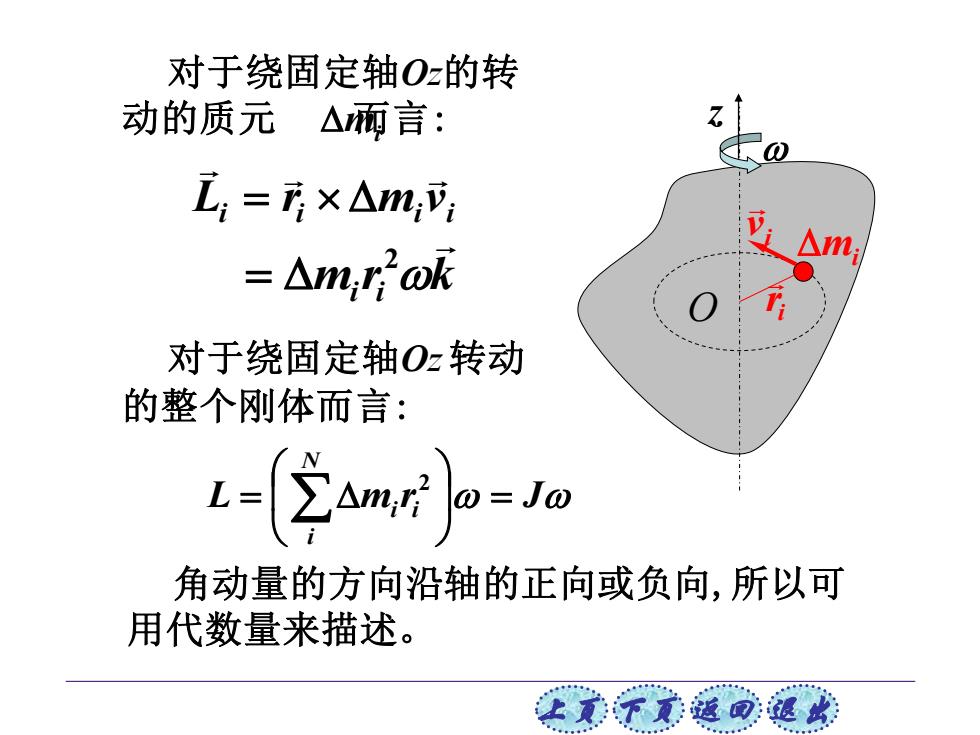
对于绕固定轴Oz的转 动的质元 △而言: Z:=i×△m;: =△,of 对于绕固定轴Oz转动 的整个刚体而言: u-2a加=n 角动量的方向沿轴的正向或负向,所以可 用代数量来描述。 让美下觉返司速此
上页 下页 返回 退出 L i i i i L r m v = mi ri k 2 = 对于绕固定轴Oz转动 的整个刚体而言: 对于绕固定轴Oz的转 动的质元 而言: mi L m r J N i i i = = 2 角动量的方向沿轴的正向或负向,所以可 用代数量来描述。 i r mi i v z O

二、定轴转动刚体的角动量定理 do M= d(Jo)dL dt dr 微分形式:Mdt=d(Jo)=dL 积分形式:Mt=Jw-Jo 或:∫Mdt=L-L 上意不家返可退此
上页 下页 返回 退出 d d M J t = d ( ) d J t = d d L t = 微分形式:M t J L d d d = = ( ) 0 0 d t t M t J J = − 积分形式: 0 0 d t t M t L L = − 或 : 二、 定轴转动刚体的角动量定理

三、定轴转动刚体的角动量守恒定律 由定轴转动定理:M= d(Jo) dt 当M=0时 d(J@)=0 dr 即 J0=J00=常量 刚体在定轴转动中,当对转轴的合外力矩为 零时,刚体对转轴的角动量保持不变,这一规律 就是定轴转动的角动量守恒定律。 让美觉返司退
上页 下页 返回 退出 d( ) d J M t = 当 M=0 时 刚体在定轴转动中,当对转轴的合外力矩为 零时,刚体对转轴的角动量保持不变, 这一规律 就是定轴转动的角动量守恒定律。 由定轴转动定理: d( ) 0 d J t = 即 J = J0 0 =常量 三、 定轴转动刚体的角动量守恒定律

讨论: a.对于绕固定转轴转动的刚体,因J保持不变, 当合外力矩为零时,其角速度恒定。 当M.=0时,J=常 0=常量 量 b.若系统由若干个刚体构成,当合外力矩为零时,系 统的角动量依然守恒。J大→小,J小→ 当M。=0时,L=J1@,+J2@2=常量
上页 下页 返回 退出 a.对于绕固定转轴转动的刚体,因J保持不变, 当合外力矩为零时,其角速度恒定。 J =常 量 =常量 b.若系统由若干个刚体构成,当合外力矩为零时,系 统的角动量依然守恒。J 大→ 小,J 小→ 大 。 L J J z = + = 1 1 2 2 常量 讨论: 0 当 M z = 时, 0 当 M z = 时
例如:花样滑冰运动员 的“旋”动作 再如:跳水运动员的“团 身一展体”动作 让美觉返司退
上页 下页 返回 退出 再如:跳水运动员的“团 身-展体”动作 例如:花样滑冰运动员 的“旋”动作
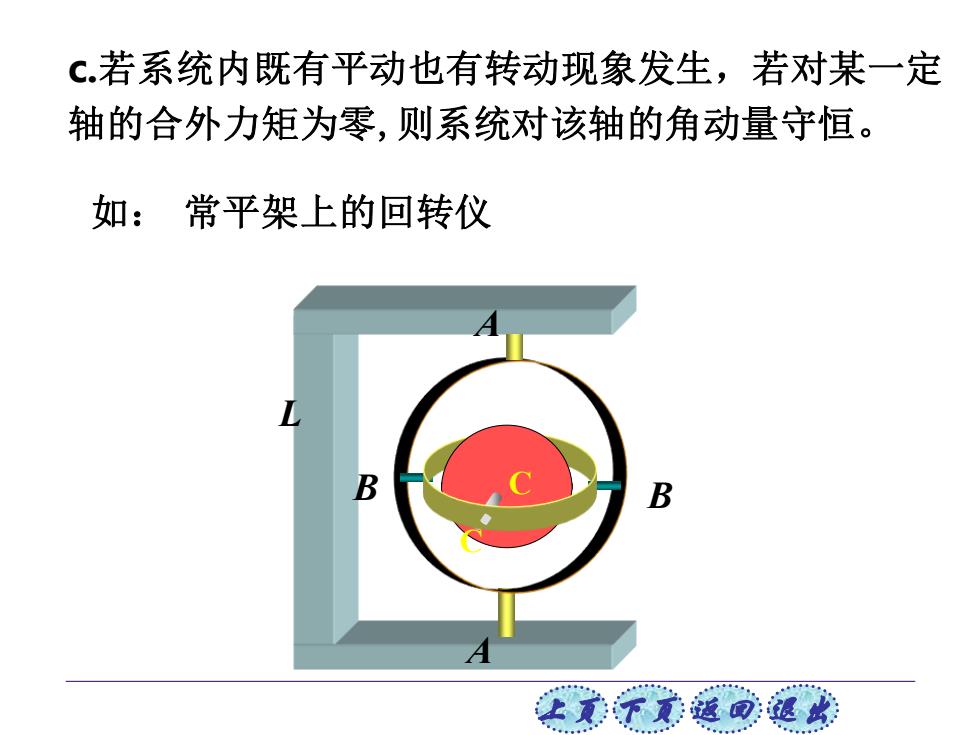
c若系统内既有平动也有转动现象发生,若对某一定 轴的合外力矩为零,则系统对该轴的角动量守恒。 如:常平架上的回转仪 B 让无子文道回退此
上页 下页 返回 退出 L A B A B C C 如: 常平架上的回转仪 c.若系统内既有平动也有转动现象发生,若对某一定 轴的合外力矩为零,则系统对该轴的角动量守恒

刚体的平动和定轴转动中的一些重要公式 刚体的平动 刚体的定轴转动 v=dx a= do do de 0= Q= di dt dt2 dt dt dt2 p=mv =m2 1 L=Jo Ex=-J02 F m M dA=Fdx Fdt dA=Md0 Mdt F=ma M=Ja Fdt=p-Po [Mdt=L-Lo ∫Fdx=mm2 m哈 ∫Md0=Jo2 王觉下元菠面:退收
上页 下页 返回 退出 刚体的平动和定轴转动中的一些重要公式 刚体的平动 刚体的定轴转动 t x v d d = 2 2 d d d d t x t v a = = d t d = 2 2 d d d d t t = = p mv = 2 k 1 2 E mv = L = J 2 k 1 2 E J = F m M J d A = F d x F dt d A = M d M dt F = ma M J = 0 F t p p d = − = − 0 M dt L L = − 2 0 2 2 1 2 1 F d x mv mv = − 2 0 2 2 1 2 1 M d J J

例题3-7一匀质细棒长为l,质量为,可绕通过其 端点O的水平轴转动,如图所示。当棒从水平位置 自由释放后,它在竖直位置上与放在地面上的物体 相撞。该物体的质量也为m,它与地面的摩擦因数 为4。相撞后物体沿地面滑行一距离s而停止。求相 撞后棒的质心C离地面的最大高度,并说明棒在 碰撞后将向左摆或向右摆的条件。 解:这个问题可分为三个阶段 进行分析。第一阶段是棒自由 摆落的过程。这时除重力外, C 其余内力与外力都不作功,所 以机械能守恒。我们把棒在竖 直位置时质心所在处取为势能
上页 下页 返回 退出 例题3-7 一匀质细棒长为l,质量为m,可绕通过其 端点O的水平轴转动,如图所示。当棒从水平位置 自由释放后,它在竖直位置上与放在地面上的物体 相撞。该物体的质量也为m,它与地面的摩擦因数 为。相撞后物体沿地面滑行一距离s而停止。求相 撞后棒的质心C离地面的最大高度h,并说明棒在 碰撞后将向左摆或向右摆的条件。 解:这个问题可分为三个阶段 进行分析。第一阶段是棒自由 摆落的过程。这时除重力外, 其余内力与外力都不作功,所 以机械能守恒。我们把棒在竖 直位置时质心所在处取为势能 C O

零点,用o表示棒这时的角速度,则 me35o-3mr。 (1) 第二阶段是碰撞过程。因碰撞时间极短,自由的 冲力极大,物体虽然受到地面的摩擦力,但可以忽 略。这样,棒与物体相撞时,它们组成的系统所受 的对转轴O的外力矩为零,所以,这个系统的对O轴 的角动量守恒。我们用表示物体碰撞后的速度,则 3 m2 o-mtmt2 jeo (2)〉 式中o'为棒在碰撞后的角速度,它可正可负。o 取正值,表示碰后棒向左摆;反之,表示向右摆。 让美觉返司退
上页 下页 返回 退出 零点,用表示棒这时的角速度,则 2 2 2 3 1 2 1 2 1 2 = J ml l mg = (1) 第二阶段是碰撞过程。因碰撞时间极短,自由的 冲力极大,物体虽然受到地面的摩擦力,但可以忽 略。这样,棒与物体相撞时,它们组成的系统所受 的对转轴O的外力矩为零,所以,这个系统的对O轴 的角动量守恒。我们用v表示物体碰撞后的速度,则 (2) = + 2 2 3 1 3 1 ml mvl ml 式中 ’为棒在碰撞后的角速度,它可正可负。′ 取正值,表示碰后棒向左摆;反之,表示向右摆