
§2-2动量定理 动量守恒定律 一、动量定理 重写牛顿第二定律的微分形式 Fdt-dp 考虑一过程,时间从到2,两端积分 Fdt=∫d方=p2-p 左侧积分表示力对时间的累积量,叫做冲量。 于是得到积分形式 亚=币2-p 江觉子觉返司退欢
上页 下页 返回 退出 重写牛顿第二定律的微分形式 = 2 1 2 1 d d p p F p t t t 考虑一过程,时间从t1到t2,两端积分 F p dt = d p2 p1 = − 一、 动量定理 左侧积分表示力对时间的累积量,叫做冲量。 = 2 1 d t t I F t 于是得到积分形式 2 1 I p p = − §2-2 动量定理 动量守恒定律

这就是质点的动量定理:物体在运动过程中所受 到的合外力的冲量,等于该物体动量的增量。 动量定理的几点说明: (1)冲量的方向: 冲量的方向一般不是某一瞬时力的方向,而是 所有元冲量F的合矢量∫疗d的方向。 (2)在直角坐标系中将矢量方程改为标量方程 (Is =Sh Fx dt=mvzx -mvis I,=∫F,dt=y2y-my I.=5 F:dt=mv2:-mvi: 让意了意返可退收
上页 下页 返回 退出 这就是质点的动量定理:物体在运动过程中所受 到的合外力的冲量,等于该物体动量的增量。 动量定理的几点说明: (1)冲量的方向: 冲量 的方向一般不是某一瞬时力 的方向,而是 所有元冲量 的合矢量 的方向。 I Fi F dt 2 1 d t t F t (2)在直角坐标系中将矢量方程改为标量方程 x x t I x t Fx t mv2 mv1 2 1 = d = − y y t I y t Fy t mv2 mv1 2 1 = d = − z z t I z t F z t mv2 mv1 2 1 = d = −

(3)动量定理在打击或碰撞问题中用来求平均力。 打击或碰撞,力的方向保持 不变,曲线与轴所包围的面积就 是t到t2这段时间内力雨冲量的 大小,根据改变动量的等效性, 得到平均力。 将积分用平 均力代替 FasF 动量定 理写为 FAI=AP 平均力写为 斥-炉 △t 平均力大小:F= t-t 江美觉返司退
上页 下页 返回 退出 (3)动量定理在打击或碰撞问题中用来求平均力。 t 2 t 1 t − F 打击或碰撞,力 的方向保持 F 不变,曲线与t轴所包围的面积就 是t1到t2这段时间内力 的冲量的 大小,根据改变动量的等效性, 得到平均力。 F F F t p = 2 1 t t F t F t d p F t = 将积分用平 均力代替 动量定 理写为 平均力写为 2 1 2 1 d t t F t F t t = − 平均力大小:
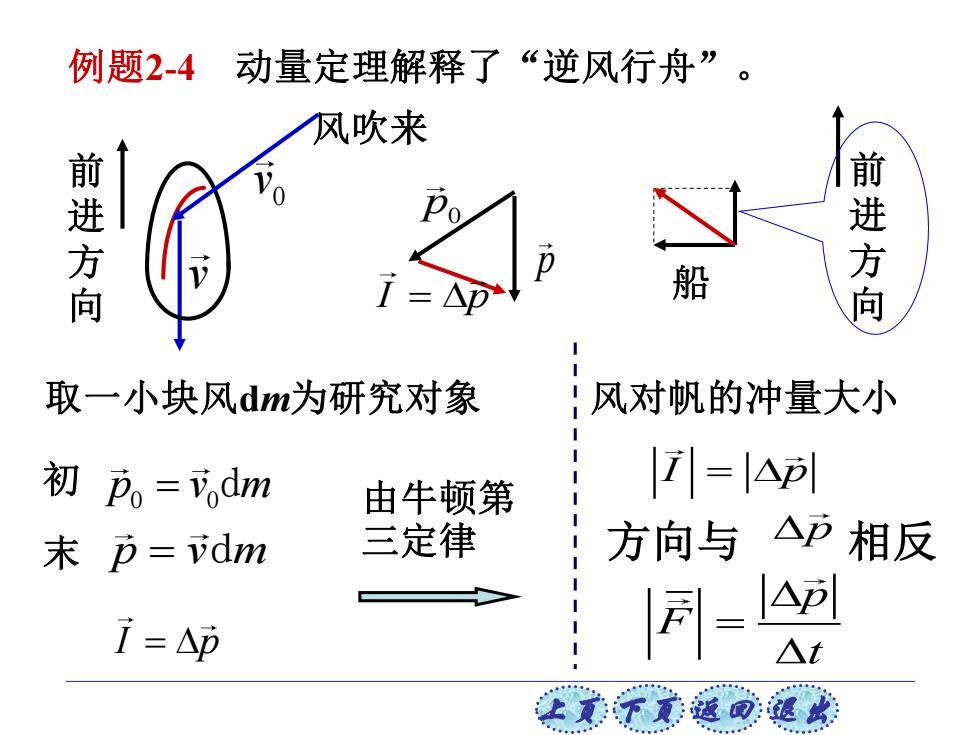
例题2-4动量定理解释了“逆风行舟”。 风吹来 进方 前进方 船 取一小块风dm为研究对象 !风对帆的冲量大小 初p。=d山m 由牛顿第 |=lA列 末币=dm 三定律 方向与 △p相反 AP 1=Ap △t
上页 下页 返回 退出 例题2-4 动量定理解释了“逆风行舟”。 船 前 进 方 向 风吹来 取一小块风dm为研究对象 0 v v p0 p I p = I p = 0 0 初 p v m = d 末 p v m = d 由牛顿第 三定律 前 进 方 向 风对帆的冲量大小 I p = 方向与 p 相反 p F t =

例题2-5质量=3t的重锤,从高度h=1.5m处自由落 到受锻压的工件上,工件发生形变。如果作用的时间 (1)=0.1s,(2)=0.01s。试求锤对工件的平均冲力。 解:以重锤为研究对象,分析受力,作受力图: 解法一锤对工件的冲力变化范 围很大,采用平均冲力计算,其反 作用力用平均支持力代替。 在竖直方向利用动量定理,取竖直 向上为正。 (F-mg)t =mv-mvo 初状态动量为m√2gh 末状态动量为0 美子元道回:退来
上页 下页 返回 退出 例题2-5 质量m=3t的重锤,从高度h=1.5m处自由落 到受锻压的工件上,工件发生形变。如果作用的时间 (1)t=0.1s, (2)t=0.01s。试求锤对工件的平均冲力。 解:以重锤为研究对象,分析受力,作受力图: 解法一 锤对工件的冲力变化范 围很大,采用平均冲力计算,其反 作用力用平均支持力代替。 在竖直方向利用动量定理,取竖直 向上为正。 N 0 ( ) F mg t mv mv − = − 初状态动量为 m gh 2 末状态动量为0 FN mg

得到(瓦-mg)t=-mV2gh 解得元=mg+m√2gh/t 代入m、h、的值,求得 (1)F=1.92×105N (2)F=1.9×10N 让美子意通回退此
上页 下页 返回 退出 N 得到 ( ) 2 F mg t m gh − = − N 解得 F mg m gh t = + 2 / 代入m、h、t的值,求得 (1) 5 N F = 1.92 10 N 6 N (2) F = 1.9 10 N

解法二考虑从锤自由下落到静止的整个过 程,动量变化为零。 重力作用时间为t+√2h/g 支持力的作用时间为t 根据动量定理,整个过程合外力的冲量为零, 即 Ft-mg(t+√2h/g)=0 得到解法一相同的结果 Fs mg+m2gh/t 江觉子觉返司退欢
上页 下页 返回 退出 解法二 考虑从锤自由下落到静止的整个过 程,动量变化为零。 重力作用时间为 t h g + 2 / 支持力的作用时间为 t 根据动量定理,整个过程合外力的冲量为零, N F t mg t h g − + = ( 2 / ) 0 得到解法一相同的结果 N F mg m gh t = + 2 / 即
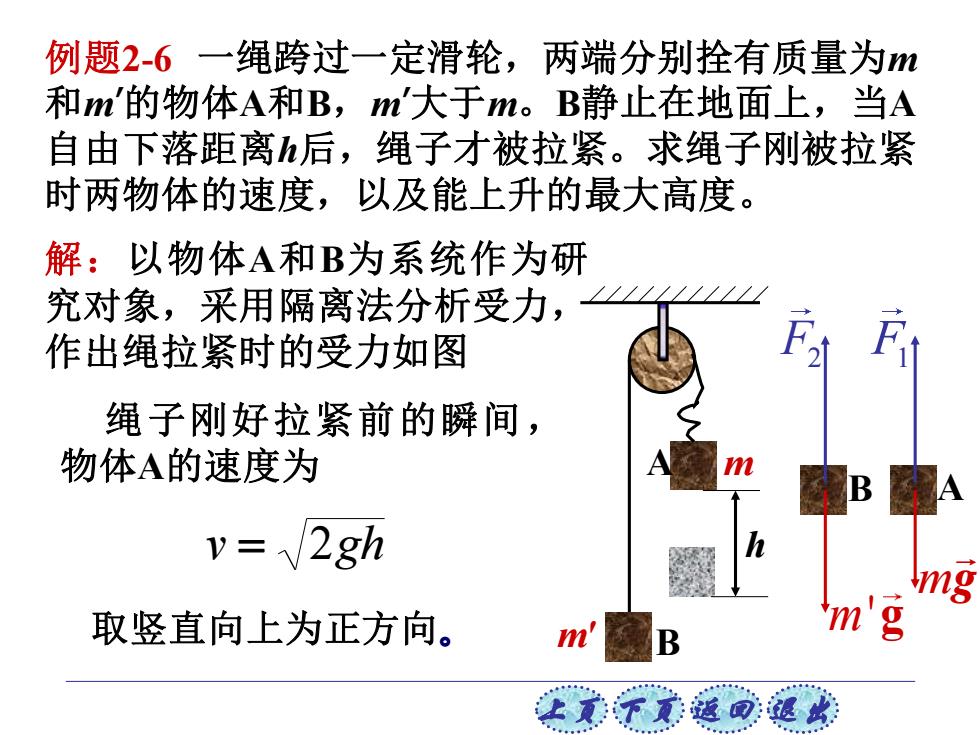
例题2-6一绳跨过一定滑轮,两端分别拴有质量为m 和m'的物体A和B,m'大于m。B静止在地面上,当A 自由下落距离后,绳子才被拉紧。求绳子刚被拉紧 时两物体的速度,以及能上升的最大高度。 解:以物体A和B为系统作为研 究对象,采用隔离法分析受力, 作出绳拉紧时的受力如图 绳子刚好拉紧前的瞬间, 物体A的速度为 y=2gh 取竖直向上为正方向。 m' 'm'g 上下返回退此
上页 下页 返回 退出 例题2-6 一绳跨过一定滑轮,两端分别拴有质量为m 和m ’的物体A和B,m ’大于m。B静止在地面上,当A 自由下落距离h后,绳子才被拉紧。求绳子刚被拉紧 时两物体的速度,以及能上升的最大高度。 m′ m B A h 解:以物体A和B为系统作为研 究对象,采用隔离法分析受力, 作出绳拉紧时的受力如图 A g m F1 B m'g F2 绳子刚好拉紧前的瞬间, 物体A的速度为 v = 2gh 取竖直向上为正方向

绳子拉紧后,经过短暂时间的作用,两物体速率 相等,对两个物体分别应用动量定理,得到 (E-ng)△t=-u-(-mv) (F,-m'g)△t=m'u-0 忽略重力,考虑到绳不可伸长,有 F=E 解得 m√2gh u= m'+m 当物体B上升速度为零时,达到最大高度 2aH=u2-0 m'-m m2h H= a= 8— m'+m m2-m2 王美不美菠回:退收
上页 下页 返回 退出 绳子拉紧后,经过短暂时间的作用,两物体速率 相等,对两个物体分别应用动量定理,得到 1 ( ) ( ) F mg t mu mv − = − − − 2 ( ' ) ' 0 F m g t m u − = − 忽略重力,考虑到绳不可伸长,有 F F 1 2 = 解得 m gh 2 u m m = + 当物体B上升速度为零时,达到最大高度 2 2 0 aH u = − m m a g m m − = + 2 2 2 m h H m m = −
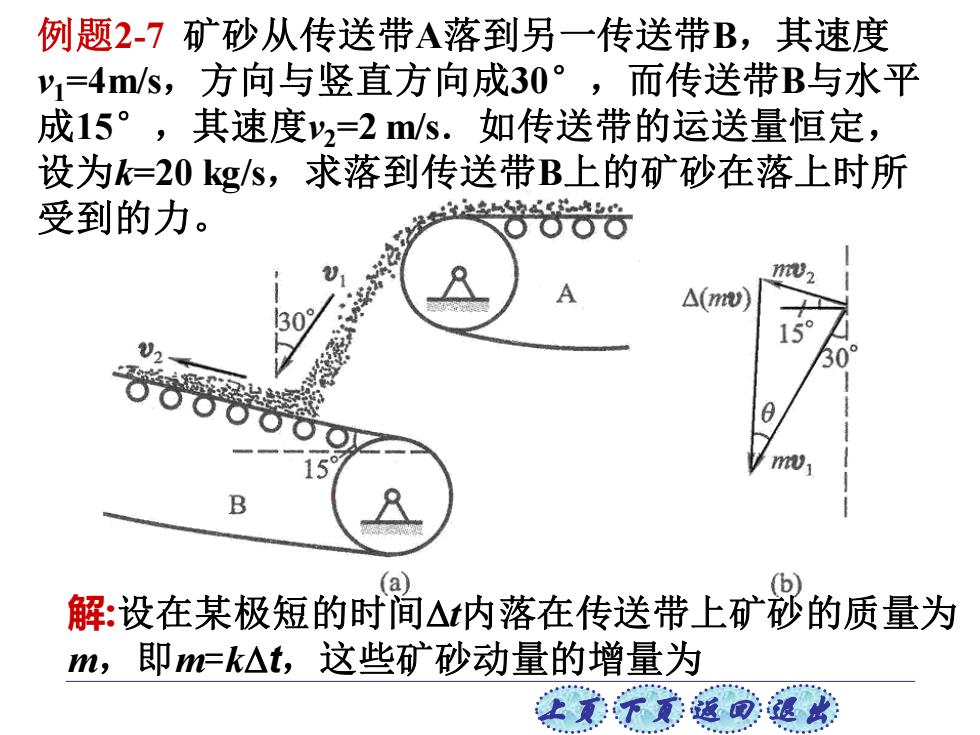
例题2-7矿砂从传送带A落到另一传送带B,其速度 1=4m/s,方向与竖直方向成30°,而传送带B与水平 成15°,其速度y2=2m/s.如传送带的运送量恒定, 设为=20kgs,求落到传送带B上的矿砂在落上时所 受到的力。 102 △(w) 15 309 B a b 解:设在某极短的时间△内落在传送带上矿秘的质量为 m,即m=k公t,这些矿砂动量的增量为 让文子意返回退此
上页 下页 返回 退出 例题2-7 矿砂从传送带A落到另一传送带B,其速度 v1=4m/s,方向与竖直方向成30°,而传送带B与水平 成15°,其速度v2=2 m/s.如传送带的运送量恒定, 设为k=20 kg/s,求落到传送带B上的矿砂在落上时所 受到的力。 解:设在某极短的时间t内落在传送带上矿砂的质量为 m,即m=kt,这些矿砂动量的增量为