
§1-2圆周运动和一般曲线运动 一、切向加速度和法向加速度 1.自然坐标系 设质点绕圆心在作变速圆周运动, 在其上任意选一点可建立如下坐标系, 其中一根坐标轴沿轨迹在该点P的切 . 线方向,该方向单位矢量用e表录; 0 另一坐标轴沿该点轨迹的法线并指向 e 曲线凹侧,相应单位矢量用e表录, 这就叫自然坐标系。 显然,沿轨迹上各点,自然坐标轴的方位是不断变 化着的
上页 下页 返回 退出 设质点绕圆心在作变速圆周运动, 在其上任意选一点可建立如下坐标系, 其中一根坐标轴沿轨迹在该点P 的切 线方向,该方向单位矢量用et 表示; 另一坐标轴沿该点轨迹的法线并指向 曲线凹侧,相应单位矢量用en表示, 这就叫自然坐标系。 → → t e n e t e n e 一、切向加速度和法向加速度 显然,沿轨迹上各点,自然坐标轴的方位是不断变 化着的。 1.自然坐标系 P §1-2 圆周运动和一般曲线运动

2.切向加速度和法向加速度 v+d 时刻:A点 t什d时刻:B点立+d) dt时间内经过弧长ds ds对应圆心角角度d0 dr=dse= dr ds 因为 dt dt 所以a= dv d dt e为单位矢量,大小不变,但方向改变 让文下元道回退此
上页 下页 返回 退出 B R d A v v v +d et 为单位矢量, 大小不变,但方向改变 2.切向加速度和法向加速度 t t d d d d r s v e ve t t = = = d d t 因为 r se = t d d ( ) d d v a v t e t t 所以 = = t时刻:A点 t+dt时刻:B点 dt时间内经过弧长ds ds对应圆心角角度d v v +d v
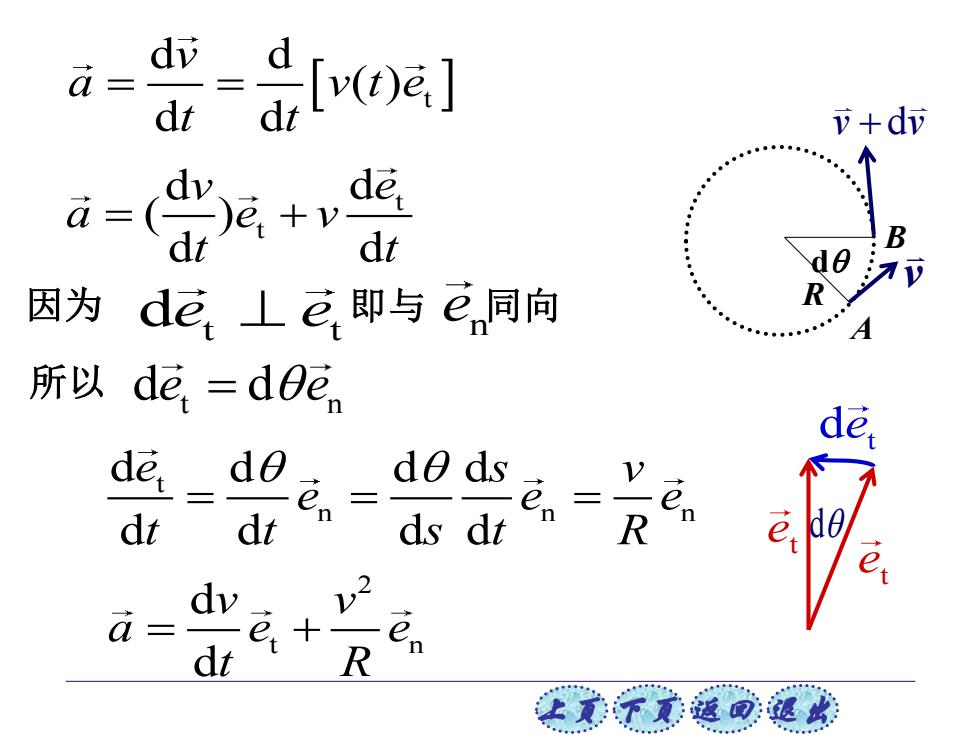
d d a= dt d [(t)e] v+dv dv a= d + de, dt 因为 de⊥e即与en同向 所以de=dde。 de de, do dθds dt dt en= ds dt en= R e dv e dt R 让意了意适回退块
上页 下页 返回 退出 t d d ( ) d d v a v t e t t = = t n n n d d d d d d d d e s v e e e t t s t R = = = 2 t n d d v v a e e t R = + d t e t e t e d t t d d ( ) d d v e a e v t t = + 即与 en 同向 B R d A v v v +d 因为 de e t t ⊥ t n 所以 d d e e =

圆周运动中的 切向加速度4和 D 法向加速度4n dv dv e, dt 力 &,=ad +a e,a=ya"ta 切向加速度改变速度的大小,法向加速度改变速 度的方向。 让美觉返司退
上页 下页 返回 退出 圆周运动中的 切向加速度at和 法向加速度an 2 t n d d v v a e e t R = + t d d v a t = 2 n v a R = 2 2 t n , a a a = + 切向加速度改变速度的大小,法向加速度改变速 度的方向。 2 t n t t n n d d v v a e e a e a e t R = + = +
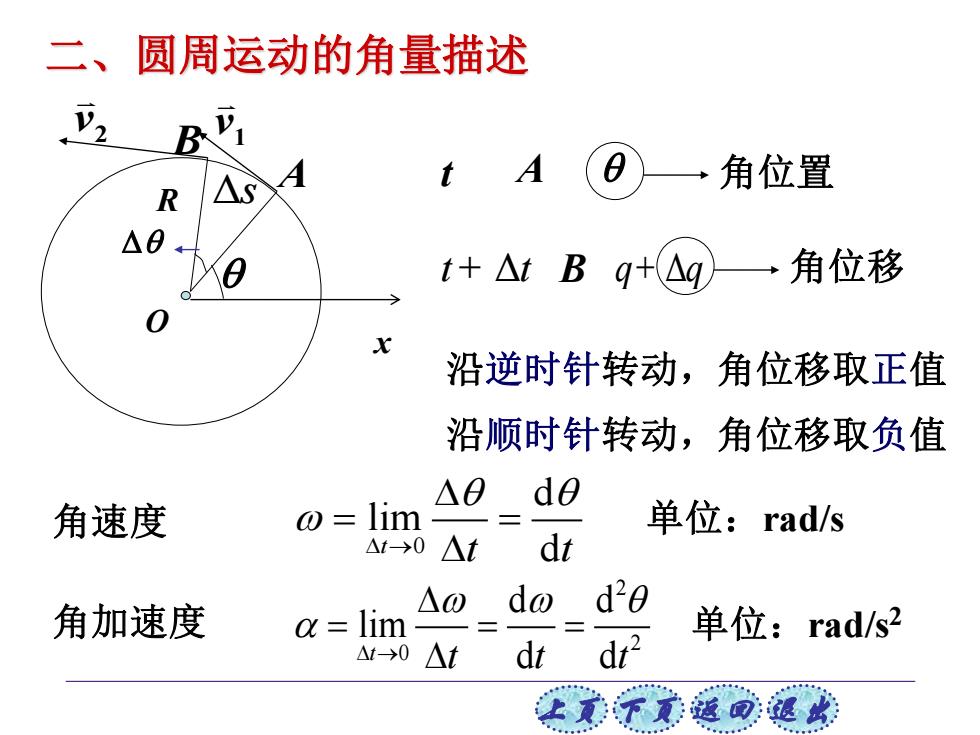
二、 圆周运动的角量描述 A →角位置 t+△tBq+△g →角位移 沿逆时针转动,角位移取正值 沿顺时针转动,角位移取负值 △0d0 角速度 @lim 单位:rad/s △f-→0△t dt 角加速度 △0 do d20 a lim 单位:rad/s2 △10△t dt dr2
上页 下页 返回 退出 O x R 1 v 2 v Δs A B t A t t + Δ B q q + Δ 角位移 沿逆时针转动,角位移取正值 沿顺时针转动,角位移取负值 角位置 角速度 角加速度 0 d lim t t t d → = = 单位:rad/s 2 2 0 d d lim t t t t d d → = = = 单位:rad/s2 二、圆周运动的角量描述

讨论: 匀速圆周运动 o是恒量 d6=odt一d6=odt一8=8,+o 匀角加速圆周运动 O是恒量 0=o,+0t 02 -o=2ax(0-0。) 一般圆周运动 d0=odt一 =8+∫0od 让美觉返司退
上页 下页 返回 退出 匀角加速圆周运动 是恒量 0 = + t 2 0 0 1 2 = + +t t 0 0 d d t t = 0 0 d t = + t 一般圆周运动 2 2 − = − 0 0 2 ( ) 匀速圆周运动 是恒量 d d = t 0 0 d d t t = = +t 0 讨论:
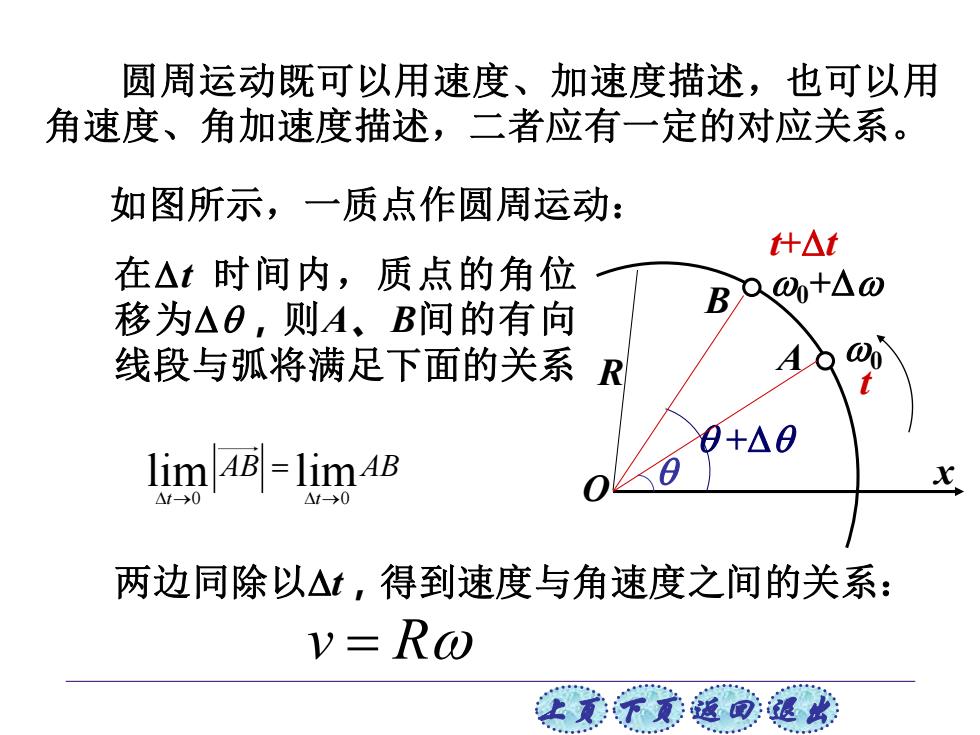
圆周运动既可以用速度、加速度描述,也可以用 角速度、角加速度描述,二者应有一定的对应关系。 如图所示,一质点作圆周运动: 什△t 在△t时间内,质点的角位 B0@+△0 移为△O,则A、B间的有向 线段与弧将满足下面的关系R 8+△0 limB =lim 48 △t-0 两边同除以△,得到速度与角速度之间的关系: v=Ro
上页 下页 返回 退出 R O x 圆周运动既可以用速度、加速度描述,也可以用 角速度、角加速度描述,二者应有一定的对应关系。 + 0 0+ t+t B t A 如图所示,一质点作圆周运动: 在t 时间内,质点的角位 移为,则A、B间的有向 线段与弧将满足下面的关系 两边同除以t,得到速度与角速度之间的关系: v = R 0 0 lim lim t t AB AB → → =

将上式两端对时间求导,得到切向加速度与角 加速度之间的关系:☑=RC 将速度与角速度的关系代入法向加速度的定义 式,得到法向加速度与角速度之间的关系: an Ro R y Ro 线量→速度、加速度 a,Ra 角量→角速度、角加速度 a。= R@2 让意子元道回退此
上页 下页 返回 退出 将上式两端对时间求导,得到切向加速度与角 加速度之间的关系: t a R = 将速度与角速度的关系代入法向加速度的定义 式,得到法向加速度与角速度之间的关系: 2 n v a R = 2 = R 线量 速度、加速度 角量 角速度、角加速度 t 2 n v R a R a R = = =

讨论 1.a,=0,an=0 匀速直线运动 2.4,=c,an=0匀变速直线运动 3.a,=0,a=c 匀速率圆周运动 4.a≠0,an≠0 变速曲线运动 让贰了意通回
上页 下页 返回 退出 t n 1. 0 , 0 a a = = 匀速直线运动 匀变速直线运动 匀速率圆周运动 变速曲线运动 t n 2 . , 0 a c a = = t n 3. 0 , a a c = = t n 4 . 0 , 0 a a 讨论:
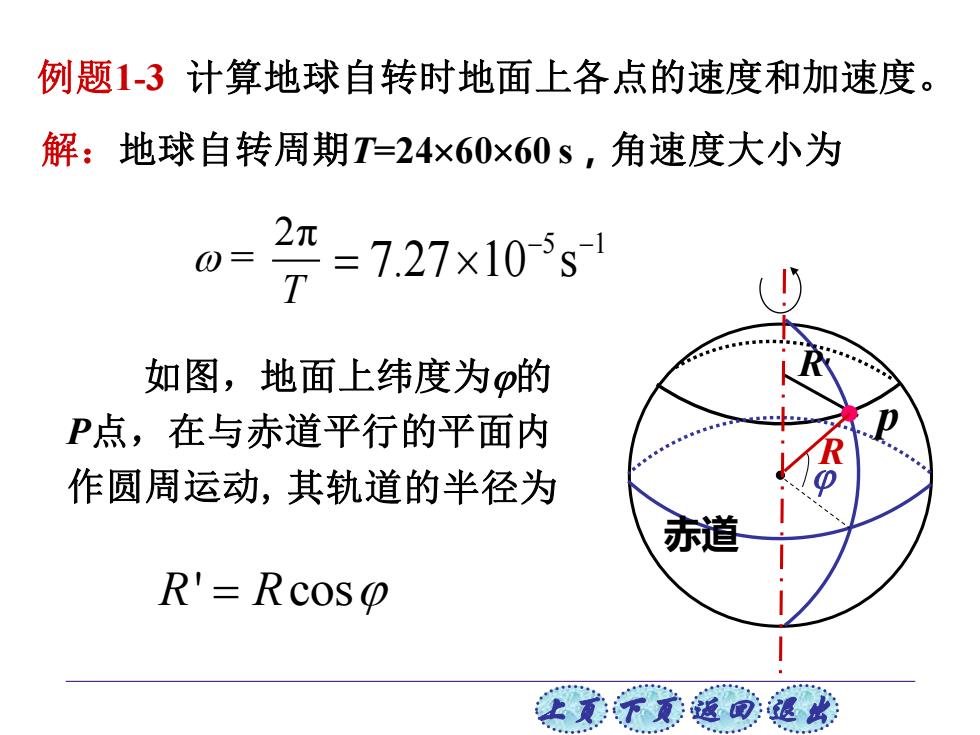
例题1-3计算地球自转时地面上各点的速度和加速度。 解:地球自转周期T-=24×60×60s,角速度大小为 2π=7.27×105s 如图,地面上纬度为p的 P点,在与赤道平行的平面内 作圆周运动,其轨道的半径为 赤道 R'=RcoSo 让美觉返司退
上页 下页 返回 退出 例题1-3 计算地球自转时地面上各点的速度和加速度。 解:地球自转周期T=246060 s,角速度大小为 2π T = 5 1 7.27 10 s − − = 如图,地面上纬度为的 P点,在与赤道平行的平面内 作圆周运动, R R ' cos = R 赤道 R′ p 其轨道的半径为