§2-7质点的角动量与角动量守恒定律 一、角动量 质点对圆心的角动量 L=pr=mvr 士美子道道意退埃
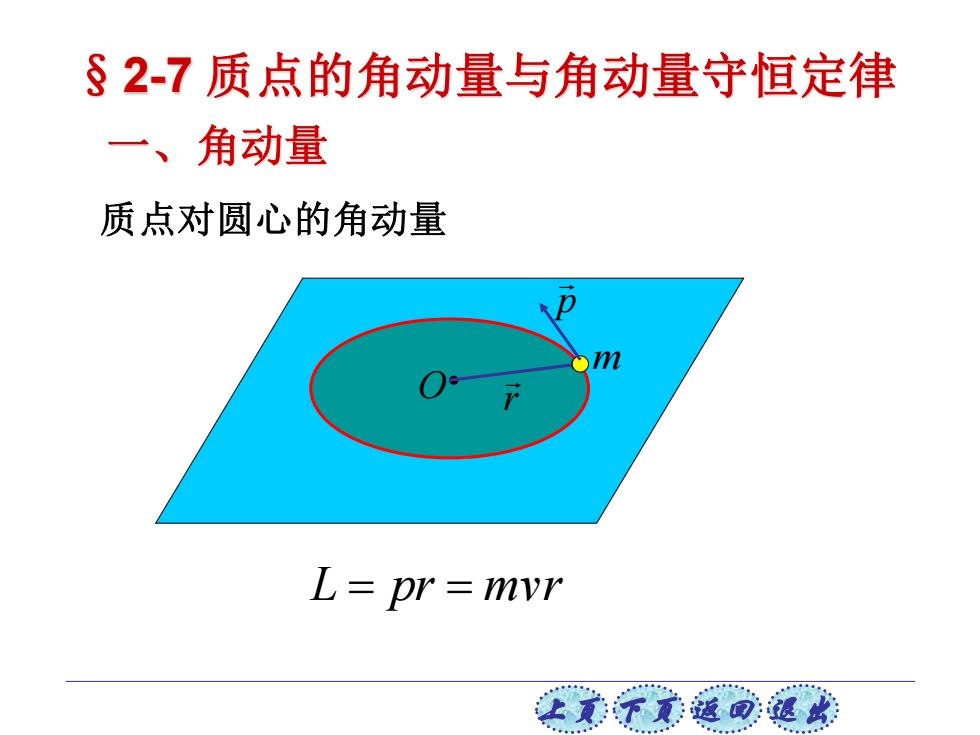
上页 下页 返回 退出 r p m O 质点对圆心的角动量 L = pr = mvr 一、角动量 §2-7 质点的角动量与角动量守恒定律
行星在公转轨道上的角动量 L=pd=prsin 让无子文道回退此
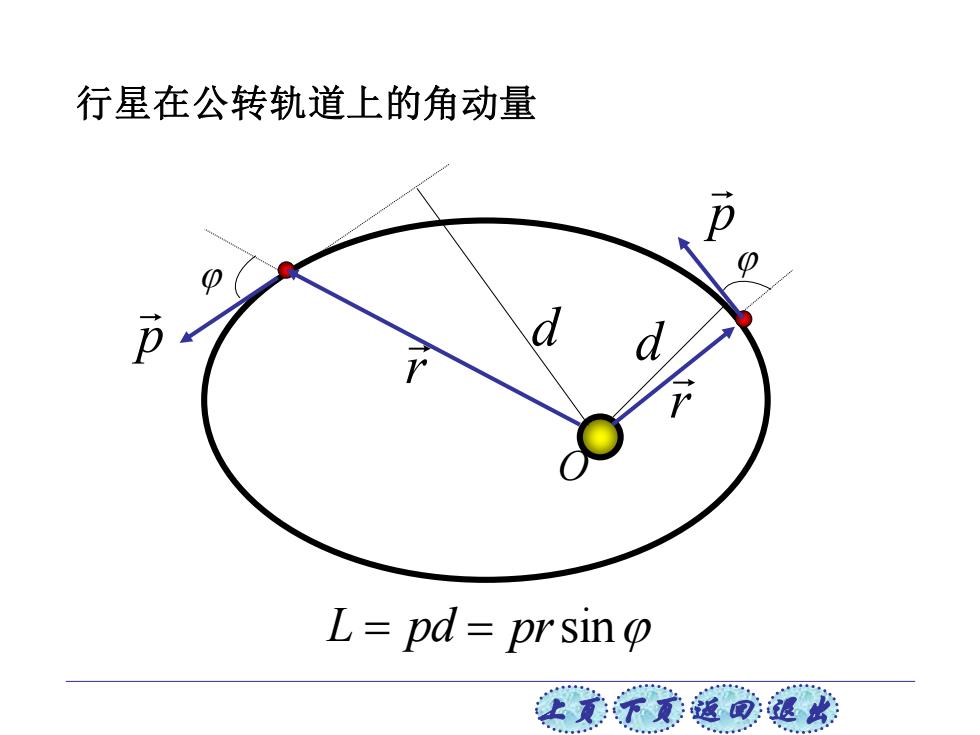
上页 下页 返回 退出 O 行星在公转轨道上的角动量 p p r r d d L = pd = prsin
定义:质点对点的角动量为 i=F×p=r×(mw) 角动量大小L=wsin ·(面积) 角动量方向 让觉不美蕴面蕴此
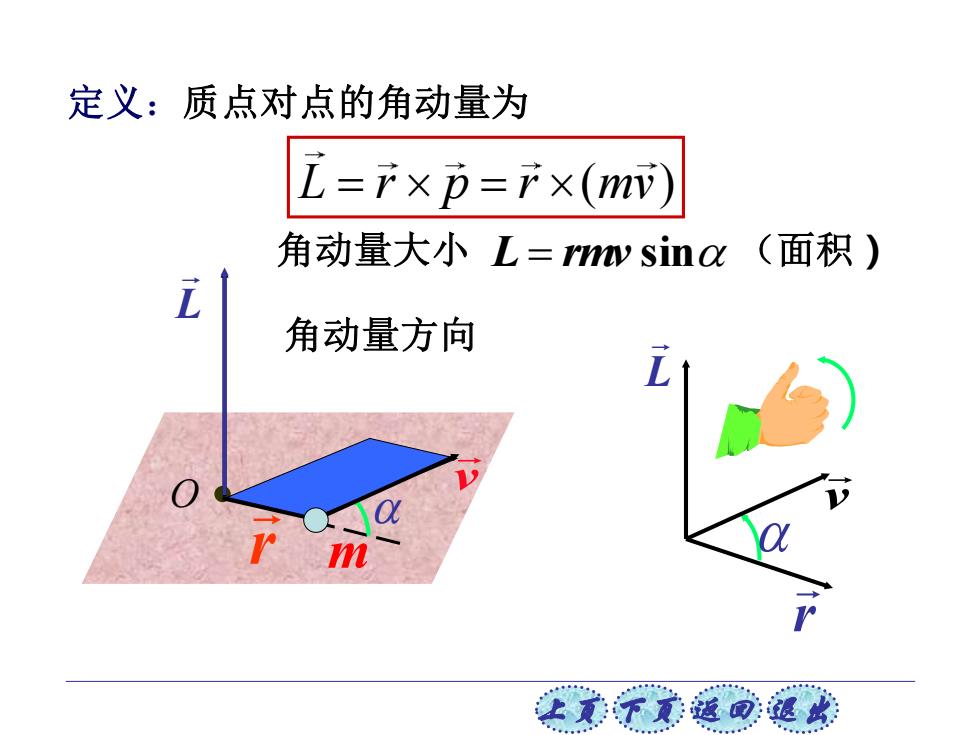
上页 下页 返回 退出 r 定义:质点对点的角动量为 O r L r p r mv = = ( ) 角动量大小 L = rmv sin (面积) L v L v m 角动量方向

讨论 (1)质点对点的角动量,不但与质点运动 有关,且与参考点位置有关。 (2)L方向的确定 上美订示返可退欢
上页 下页 返回 退出 (1)质点对点的角动量,不但与质点运动 有关,且与参考点位置有关。 (2) L 方向的确定 L v r L v r 讨论:
(3)作圆周运动时,由于下⊥卫,质点对圆心 的角动量大小为 =rmy 大小不 方向不变 质点对圆心O的角动量为恒量 让意子元返觉退此
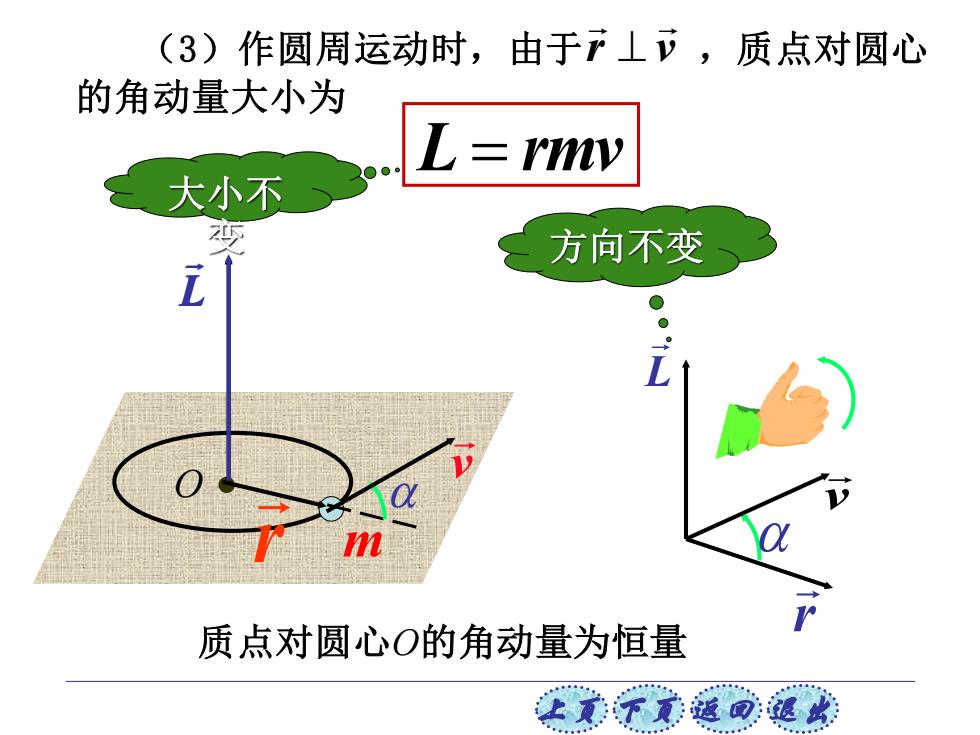
上页 下页 返回 退出 大小不 变 方向不变 r O m r v L (3)作圆周运动时,由于 ,质点对圆心 的角动量大小为 r v ⊥ L = rmv L L 质点对圆心O的角动量为恒量 v

例题2-23按经典原子理论,认为氢原子中的电子在圆 形轨道上绕核运动。电子与氢原子核之间的静电力为 F=ker2,其中e为电子或氢原子核的电荷量,r为轨道 半径,k为常量。因为电子的角动量具有量子化的特 征,所以电子绕核运动的角动量只能等于/2π的整数 (n)倍。问电子运动容许的轨道半径等于多少? 解:由牛顿第二定律得 F=k 3 =ma =m- (1) 由于电子绕核运动时,角动量具有量子化的特征,即 h L=mvr=n n=1,2,3,. (2) 2元
上页 下页 返回 退出 例题2-23 按经典原子理论,认为氢原子中的电子在圆 形轨道上绕核运动。电子与氢原子核之间的静电力为 F=ke2 /r 2,其中e为电子或氢原子核的电荷量,r为轨道 半径,k 为常量。因为电子的角动量具有量子化的特 征,所以电子绕核运动的角动量只能等于h/2的整数 (n)倍。 问电子运动容许的轨道半径等于多少? 2 2 2 n e v F k ma m r r = = = 解:由牛顿第二定律得 1, 2,3, 2π h L mvr n n = = = 由于电子绕核运动时,角动量具有量子化的特征,即 (1) (2)

由式(1)和式(2)两式,得 n2h2 4π2me2 (3) 由上式可知,电子绕核运动容许的轨道半径与平 方成正比。这就是说,只有半径等于一些特定值的 轨道才是容许的,轨道半径的量值是不连续的。 将各常量的值代人式(3),并取n=1,得最小的r值: 5=0.530×1010m 从近代物理学中知道,这一量值与用其他方法估计 得到的量值符合得很好。 让美子觉返司退此
上页 下页 返回 退出 2 2 2 2 4π n h r kme = 由式(1)和式(2)两式,得 10 1 r 0.530 10 m − = 由上式可知,电子绕核运动容许的轨道半径与n平 方成正比。这就是说,只有半径等于一些特定值的 轨道才是容许的,轨道半径的量值是不连续的。 将各常量的值代人式(3),并取n=1,得最小的r值: 从近代物理学中知道,这一量值与用其他方法估计 得到的量值符合得很好。 (3)
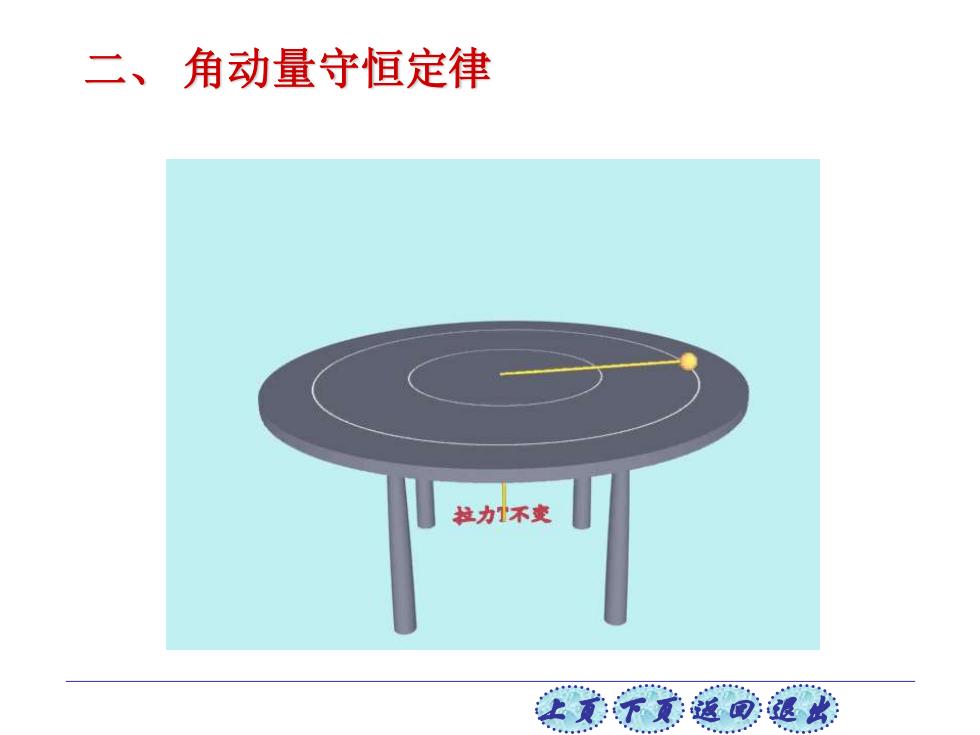
二、角动量守恒定律 拉力不变 让意子元道回退此
上页 下页 返回 退出 二、 角动量守恒定律

V2 实验中发现 V22= mvr =mv r 表明小球对圆心的角动量保持不变。 江美不觉返回退成
上页 下页 返回 退出 F 1 v 2 v 2 r 1 r o 2 2 1 1 m v r = v r 2 2 1 1 mv r = mv r 表明小球对圆心的角动量保持不变。 实验中发现

行星绕太阳的运动 pd=常量 产×币=常矢量 表明行星在运动过程中,对太阳的角动量保持不变。 让美不家返回退
上页 下页 返回 退出 行星绕太阳的运动 pd =常量 r p =常矢量 表明行星在运动过程中,对太阳的角动量保持不变。 O p p r r d d