§3-3定轴转动中的功能关系 一、力矩的功 力矩的功:当刚体在外力矩作用下绕定轴转 动而发生角位移时,就称力矩对刚体作功。 力F对P点作功: dA-F.dr =Fds cos(π/2-p) =Fdssin o ds=rdo 让美下觉返司速此
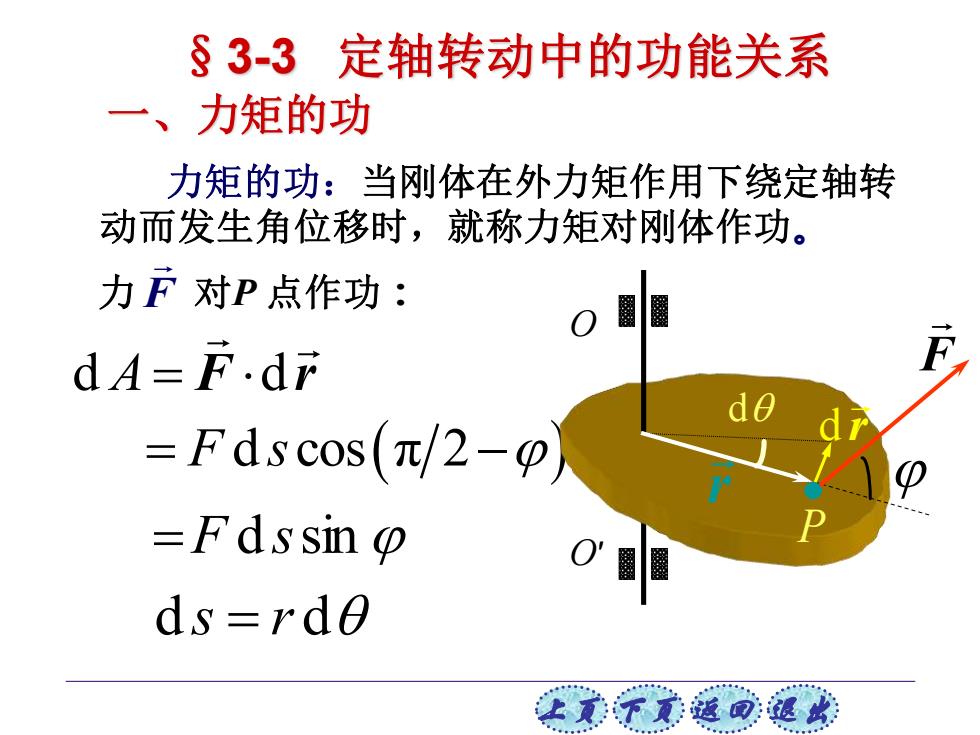
上页 下页 返回 退出 力矩的功:当刚体在外力矩作用下绕定轴转 动而发生角位移时,就称力矩对刚体作功。 力 F 对P 点作功: F r d A = d =F d ssin = − F s d cos(π 2 ) d s = r d O′ O d r F r d P §3-3 定轴转动中的功能关系 一、力矩的功
因Frsin o=M 故dA=MdO 力矩作功: A=∫Md6=心Md0 对于刚体定轴转动 情形,因质点间无相对 位移,任何一对内力作 功为零。 正贰子元道同退此
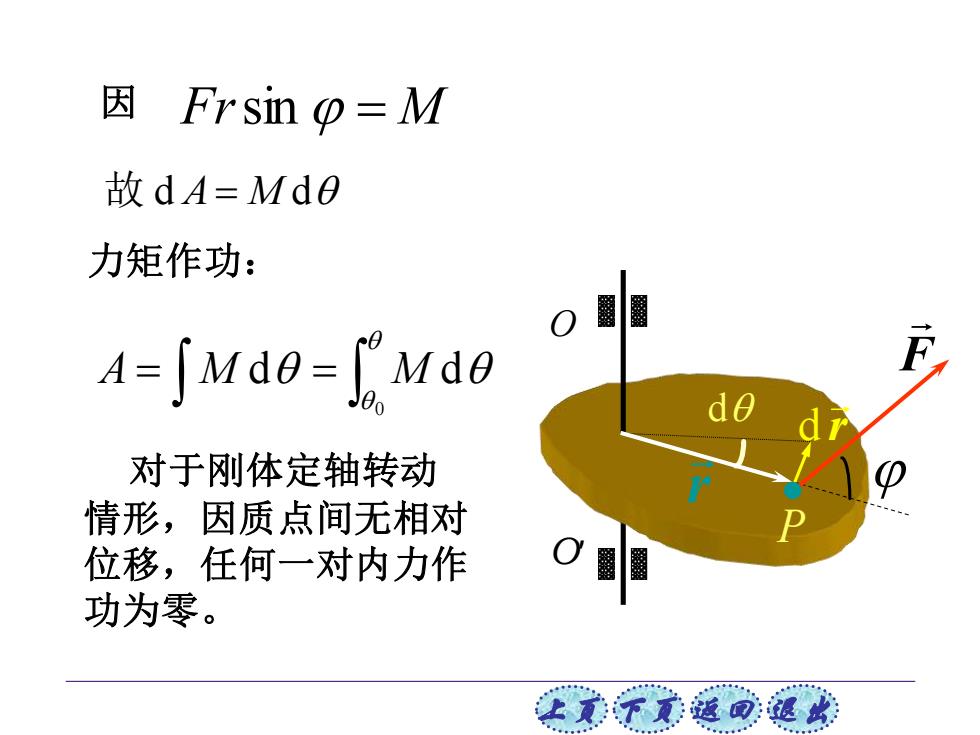
上页 下页 返回 退出 因 Frsin = M 故 d d A M= = = 0 A M d M d 力矩作功: 对于刚体定轴转动 情形,因质点间无相对 位移,任何一对内力作 功为零。 O′ O d r F r d P

二、刚体的转动动能 刚体的转动动能应该是组成刚体的各个质点 的动能之和。设刚体中第个质点的质量为△m, 速度为y,则该质点的动能为 1 △m, 2 刚体做定轴转动时,各质点的角速度相同。 设质点△m离轴的垂直距离为y,则它的线速度 v:=ar 因此整个刚体的动能为 E=∑4mg=)(∑am)o 上觉子觉道司退欢
上页 下页 返回 退出 2 2 1 i i m v 因此整个刚体的动能为 刚体的转动动能应该是组成刚体的各个质点 的动能之和。设刚体中第i个质点的质量为 , 速度为 ,则该质点的动能为 mi i v 刚体做定轴转动时,各质点的角速度相同。 设质点 mi 离轴的垂直距离为 ri ,则它的线速度 ( ) 2 2 2 k 1 1 2 2 E m v m r = = i i i i i i v =r 二、 刚体的转动动能

式中∑△m,是刚体对转轴的转动惯量2所以 上式写为 1 上式中的动能是刚体因转动而具有的动能,因 此叫刚体的转动动能。 三、定轴转动的动能定理 总外力矩对刚体所作的功为A=M0 与此对应的动能增量为 b-jJa AE=2J,2 转动的动能定理 =0=J,2-Jm
上页 下页 返回 退出 2 k 1 2 E J = 上式中的动能是刚体因转动而具有的动能,因 此叫刚体的转动动能。 式中 是刚体对转轴的转动惯量 ,所以 上式写为 2 miri J 总外力矩对刚体所作的功为 2 1 A Md = 2 1 2 2 2 1 1 1 d 2 2 A M J J = = − 2 2 k 2 1 1 1 2 2 与此对应的动能增量为 = − E J J 三、定轴转动的动能定理 转动的动能定理

四、刚体的重力势能 对于一个不太大的质量为m的物体,它的重力 势能应是组成刚体的各个质点的重力势能之和 即 E。=∑Amgh=g∑△m,h 质心高度为 2=∑4mh n 可得 E。=mghc 若只有保守力作功 E=mgh+Jo2=常量 2 让美下觉返司速此
上页 下页 返回 退出 E mgh p = C 即 质心高度为 i i C m h h m = 对于一个不太大的质量为 的物体,它的重力 势能应是组成刚体的各个质点的重力势能之和 m 1 2 2 若只有保守力作功 E mgh J = + = C 常量 四、刚体的重力势能 可得

例题3-5如图,冲床上配置一质量为5000kg的飞轮, 1=0.3m,2=0.2m。今用转速为900r/min的电动机借 皮带传动来驱动飞轮,已知电动机的传动轴直径为 d=0.1m。(1)求飞轮的转动动能。(2)若冲床冲 断0.5mm厚的薄钢 片需用冲力9.80×104N, 所消耗的能量全部由飞 2f12r2 轮提供,问冲断钢片后 飞轮的转速变为多大? 让贰不贰返可退晚
上页 下页 返回 退出 例题3-5 如图,冲床上配置一质量为5000kg的飞轮, r1=0.3m, r2=0.2m。今用转速为900r/min的电动机借 皮带传动来驱动飞轮,已知电动机的传动轴直径为 d=0.1m。(1)求飞轮的转动动能。(2)若冲床冲 断0.5 mm厚的薄钢 片需用冲力9.80104N , 所消耗的能量全部由飞 轮提供,问冲断钢片后 飞轮的转速变为多大? 2r1 2r2 d

解:(1)为了求飞轮的转动动能,需先求出它的转 动惯量和转速。因飞轮质量大部分分布在轮缘上, 由图示尺寸并近似用圆筒的转动惯量公式,得 1-g+)=325gm 皮带传动机构中,电动机的传动轴是主动轮, 飞轮是从动轮。两轮的转速与轮的直径成反比,即 飞轮的转速为 d电 飞电d飞o 2元n电 d电 由此得飞轮的角速度 60 60 d 让美下觉返同速
上页 下页 返回 退出 解:(1)为了求飞轮的转动动能,需先求出它的转 动惯量和转速。因飞轮质量大部分分布在轮缘上, 由图示尺寸并近似用圆筒的转动惯量公式,得 ( ) 2 2 2 1 2 325kg m 2 m J r r = + = 皮带传动机构中,电动机的传动轴是主动轮, 飞轮是从动轮。两轮的转速与轮的直径成反比,即 飞轮的转速为 飞 电 飞 电 d d n = n 由此得飞轮的角速度 2π 2π 60 60 n d n d = = 飞 飞 电 电

这样飞轮的转动动能是 02=405 (2)在冲断钢片过程中,冲力F所作的功为 A=Fd=49J 这就是飞轮消耗的能量,此后飞轮的能量变为 E=(40055-49)J=40006J 由-o求得此时间的角速度。为'=V 而飞轮的转速变为 o'=149.8r/min 2元
上页 下页 返回 退出 这样飞轮的转动动能是 2 k 1 40055J 2 E J = = (2)在冲断钢片过程中,冲力F所作的功为 A Fd = = 49J 这就是飞轮消耗的能量,此后飞轮的能量变为 Ek = − = (40055 49 J 40006J ) 由 k 2 求得此时间的角速度 ’为 1 2 E J = 2Ek J = 而飞轮的转速变为 1 149.8r / min 2π n 飞= =
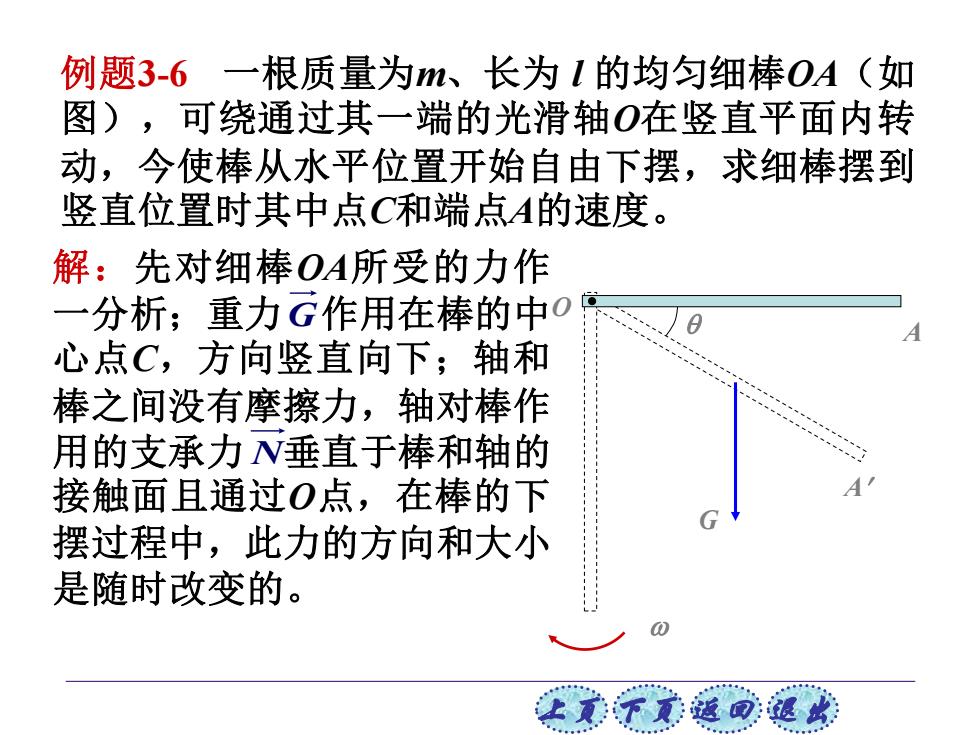
例题3-6一根质量为m、长为1的均匀细棒OA(如 图),可绕通过其一端的光滑轴O在竖直平面内转 动,今使棒从水平位置开始自由下摆,求细棒摆到 竖直位置时其中点C和端点A的速度。 解:先对细棒OA所受的力作 一分析;重力G作用在棒的中0 心点C,方向竖直向下;轴和 棒之间没有摩擦力,轴对棒作 用的支承力N垂直于棒和轴的 接触面且通过O点,在棒的下 摆过程中,此力的方向和大小 是随时改变的。 让美下元返回:退欢
上页 下页 返回 退出 解:先对细棒OA所受的力作 一分析;重力 作用在棒的中 心点C,方向竖直向下;轴和 棒之间没有摩擦力,轴对棒作 用的支承力 垂直于棒和轴的 接触面且通过O点,在棒的下 摆过程中,此力的方向和大小 是随时改变的。 N G 例题3-6 一根质量为m、长为 l 的均匀细棒OA(如 图),可绕通过其一端的光滑轴O在竖直平面内转 动,今使棒从水平位置开始自由下摆,求细棒摆到 竖直位置时其中点C和端点A的速度。 G A A O

在棒的下摆过程中,对转轴0而言,支撑力通 过0点,所以支撑力的力矩等于零,重力的力 矩则是变力矩,大小等于mg(U/2)cos0,棒转过一 极小的角位移d0时,重力矩所作的元功是 d4-mgcos 在使棒从水平位置下摆到竖直位置过程中,重力 矩所作的功是 A=∫dA=mg2cosd=mg 应该指出:重力矩作的功就是重力作的功,也可 用重力势能的差值来表示。棒在水平位置时的角 速度o=0,下摆到竖直位置时的角速度为o,按 力矩的功和转动动能增量的关系式得
上页 下页 返回 退出 d cos d 2 l A mg = 在使棒从水平位置下摆到竖直位置过程中,重力 矩所作的功是 π 2 0 d cos d 2 2 l l A A mg mg = = = 应该指出:重力矩作的功就是重力作的功,也可 用重力势能的差值来表示。棒在水平位置时的角 速度0=0,下摆到竖直位置时的角速度为,按 力矩的功和转动动能增量的关系式得 在棒的下摆过程中,对转轴O而言,支撑力 通 过O点,所以支撑力 的力矩等于零,重力 的力 矩则是变力矩,大小等于mg(l/2) cos ,棒转过一 极小的角位移d 时,重力矩所作的元功是 N G N