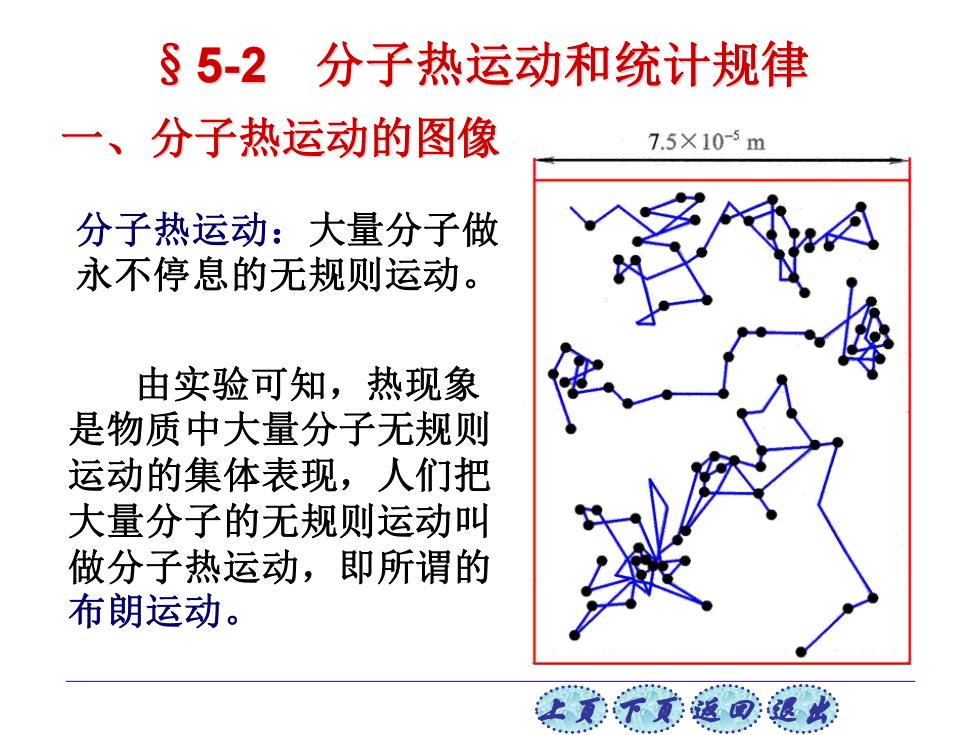
§5-2 分子热运动和统计规律 一、分子热运动的图像 7.5×10-5m 分子热运动:大量分子做 永不停息的无规则运动。 由实验可知,热现象 是物质中大量分子无规则 运动的集体表现,人们把 大量分子的无规则运动叫 做分子热运动,即所谓的 布朗运动。 让美下元返回:退欢
上页 下页 返回 退出 由实验可知,热现象 是物质中大量分子无规则 运动的集体表现,人们把 大量分子的无规则运动叫 做分子热运动,即所谓的 布朗运动。 分子热运动:大量分子做 永不停息的无规则运动。 一、分子热运动的图像 §5-2 分子热运动和统计规律

在标准状态下,对于同一物质气体的密度大约为 液体的1/1000。设液体分子是紧密排列的,则气体分 子之间的距离大约是分子本身线度(1010m)的 (1000)13倍,即10倍左右。所以把气体看作是彼此相 距很大间隔的分子集合。 在气体中,由于分子的分布相当稀疏,分子与分子 间的相互作用力,除了在碰撞的瞬间外,极其微小。 在连续两次碰撞之间分子所经历的路程平均为 10-7m,而分子的平均速率很大,约为500m/s。因此, 平均大约经过1010s,分子与分子碰撞一次,即在1s 内,一个分子将受到100次碰撞。分子碰撞的瞬间大 约是10-12s,这一时间远小于分子自由运动所经历的平 均时间(10-10s)。因此,在分子的连续两次碰撞之间, 分子的运动可看作由其惯性支配的自由运动。 让意了文道回退此
上页 下页 返回 退出 在标准状态下,对于同一物质气体的密度大约为 液体的1/1000。设液体分子是紧密排列的,则气体分 子之间的距离大约是分子本身线度(10-10 m) 的 (1000) 1/3倍,即10倍左右。所以把气体看作是彼此相 距很大间隔的分子集合。 在连续两次碰撞之间分子所经历的路程平均为 10-7 m,而分子的平均速率很大,约为500 m/s。因此, 平均大约经过10-10s,分子与分子碰撞一次,即在1s 内,一个分子将受到1010次碰撞。分子碰撞的瞬间大 约是10-12 s,这一时间远小于分子自由运动所经历的平 均时间(10-10s)。因此,在分子的连续两次碰撞之间, 分子的运动可看作由其惯性支配的自由运动。 在气体中,由于分子的分布相当稀疏,分子与分子 间的相互作用力,除了在碰撞的瞬间外,极其微小

二、分子热运动的基本特征 分子热运动的基本特征是永恒的运动与频繁 的相互碰撞。它与机械运动有本质的区别,故不 能简单应用力学定律来解决分子热运动问题。 1.无序性 某个分子的运动,是杂乱无章的,无序的; 各个分子之间的运动也不相同,即无序性;这正 是热运动与机械运动的本质区别。 让美下觉返司速此
上页 下页 返回 退出 分子热运动的基本特征是永恒的运动与频繁 的相互碰撞。它与机械运动有本质的区别,故不 能简单应用力学定律来解决分子热运动问题。 1.无序性 某个分子的运动,是杂乱无章的,无序的; 各个分子之间的运动也不相同,即无序性;这正 是热运动与机械运动的本质区别。 二、分子热运动的基本特征

2.统计性 但从大量分子的整体的角度看,存在一定 的统计规律,即统计性。 例如: 在平衡态下,气体分子的空间分布(密度) 是均匀的。(分子运动是永恒的) 可作假设:气体分子向各个方向运动的机会 是均等的,或者说沿各个方向运动的平均分子数 应相等且分子速度在各个方向的分量的统计平均 值也相等。 对大量分子体系的热平衡态,它是成立的
上页 下页 返回 退出 2.统计性 但从大量分子的整体的角度看,存在一定 的统计规律,即统计性。 例如: 在平衡态下,气体分子的空间分布(密度) 是均匀的。(分子运动是永恒的) 可作假设:气体分子向各个方向运动的机会 是均等的,或者说沿各个方向运动的平均分子数 应相等且分子速度在各个方向的分量的统计平均 值也相等。 对大量分子体系的热平衡态,它是成立的

3.统计方法 分子热运动具有无序性与统计性,与机械运动有 本质的区别,故不能简单应用力学定律来解决分子热 运动问题。必须兼顾两种特征,应用统计方法。 气体动理论中,求出大量分子的某些微观量的统 计平均值,用它来解释实验中测的宏观量,故可从实 测的宏观量了解个别分子的真实性质。 统计方法同时伴随着起伏现象。 如对气体中某体积内的质量密度的多次测量,各 次测量对平均值都有微小的偏差。当气体分子数很大 时,起伏极微小,完全可忽略;当气体分子数较小时, 起伏与平均值可比拟,不可忽略。故统计规律只适用 于大量分子的整体。 让美下元返回退欢
上页 下页 返回 退出 分子热运动具有无序性与统计性,与机械运动有 本质的区别,故不能简单应用力学定律来解决分子热 运动问题。必须兼顾两种特征,应用统计方法。 3.统计方法 气体动理论中,求出大量分子的某些微观量的统 计平均值,用它来解释实验中测的宏观量,故可从实 测的宏观量了解个别分子的真实性质。 统计方法同时伴随着起伏现象。 如对气体中某体积内的质量密度的多次测量,各 次测量对平均值都有微小的偏差。当气体分子数很大 时,起伏极微小,完全可忽略;当气体分子数较小时, 起伏与平均值可比拟,不可忽略。故统计规律只适用 于大量分子的整体
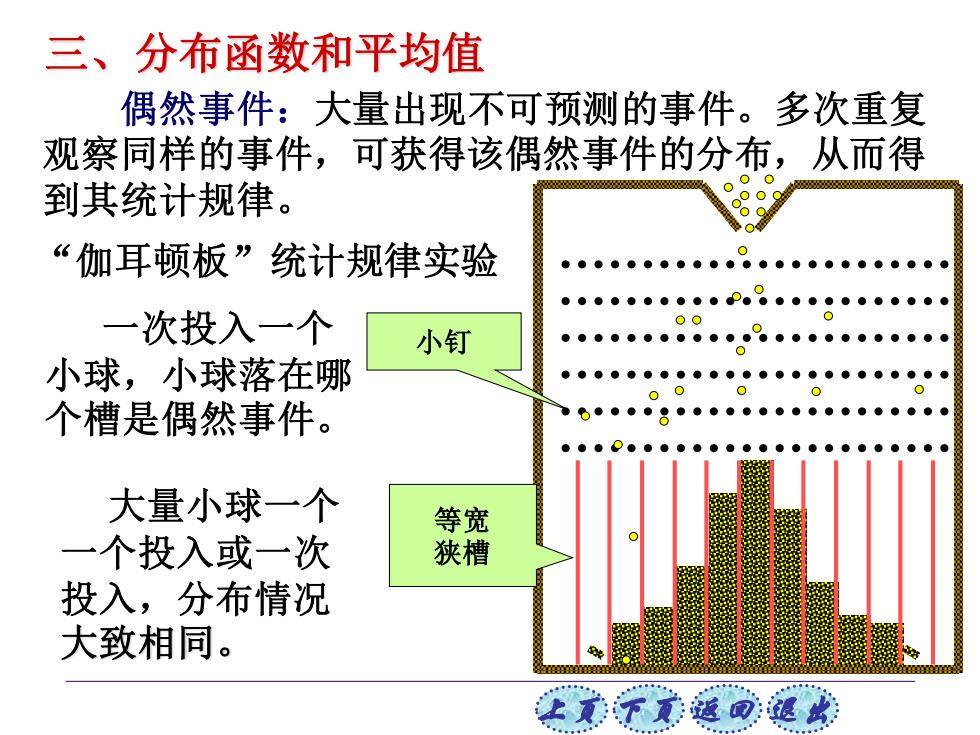
三、分布函数和平均值 偶然事件:大量出现不可预测的事件。多次重复 观察同样的事件,可获得该偶然事件的分布,从而得 到其统计规律。 89g “伽耳顿板”统计规律实验 一次投入一个 小钉 小球,小球落在哪 个槽是偶然事件。 ●● 大量小球一个 等宽 一个投入或一次 狭槽 投入,分布情况 大致相同
上页 下页 返回 退出 偶然事件:大量出现不可预测的事件。多次重复 观察同样的事件,可获得该偶然事件的分布,从而得 到其统计规律。 三、分布函数和平均值 “伽耳顿板”统计规律实验 小钉 等宽 狭槽 一次投入一个 小球,小球落在哪 个槽是偶然事件。 大量小球一个 一个投入或一次 投入,分布情况 大致相同

在一定的条件下,大量的偶然事件存在着一种必然 规律性-统计规律。 如何用数学函数来描述小球的分布呢? h 取横坐标x表示狭槽的水 平位置,纵坐标h为狭槽内 积累小球的高度。这样, 就可得到小球按狭槽分布 的一个直方图,如图(a)所 △x 示。 (a) 设第i个狭槽的宽度为△x,其中积累小球的高度为h, 则直方图中此狭槽内小球占据的面积为△A,此狭槽内小 球的数目△N,正比于此面积:△N=C△A=Ch:△x.令N为 小球总数: 让美下元返回退欢
上页 下页 返回 退出 在一定的条件下,大量的偶然事件存在着一种必然 规律性-统计规律。 如何用数学函数来描述小球的分布呢? 取横坐标x表示狭槽的水 平位置,纵坐标h为狭槽内 积累小球的高度。这样, 就可得到小球按狭槽分布 的一个直方图,如图(a)所 示。 设第i个狭槽的宽度为xi,其中积累小球的高度为hi, 则直方图中此狭槽内小球占据的面积为A,此狭槽内小 球的数目 Ni正比于此面积: N=C Ai=Chi xi .令N为 小球总数:
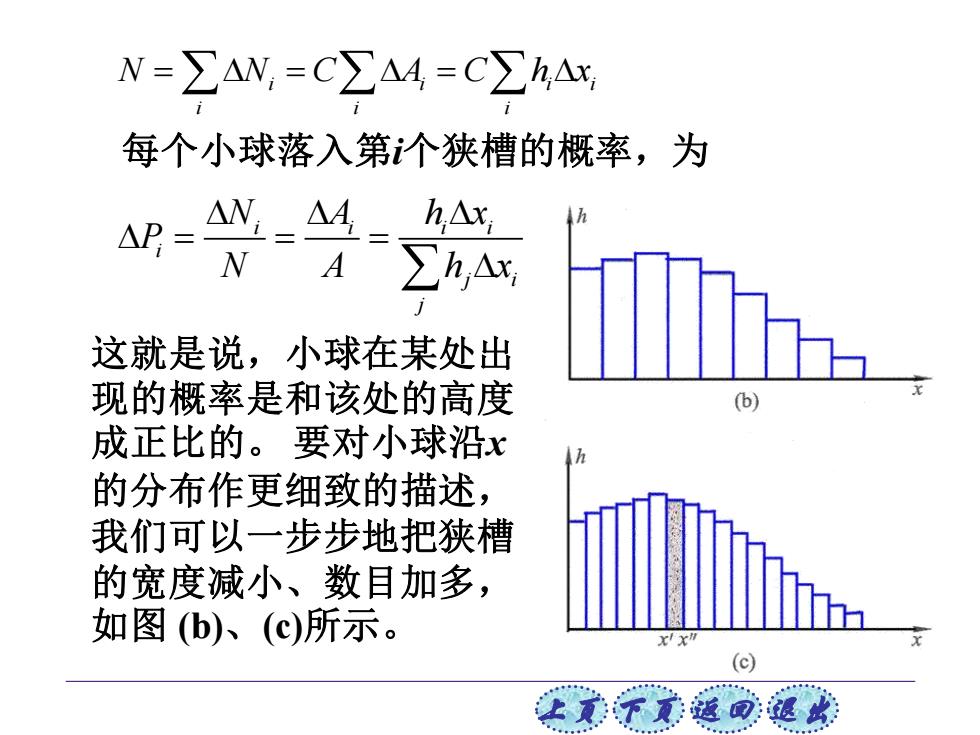
N=∑AN,=C∑A4=C∑hAx 每个小球落入第个狭槽的概率,为 △N-△4-h△x N A∑h,Ax 这就是说,小球在某处出 现的概率是和该处的高度 成正比的。要对小球沿x 的分布作更细致的描述, 我们可以一步步地把狭槽 的宽度减小、数目加多, 如图(b)、(c)所示。 (c
上页 下页 返回 退出 i i i i i i i N N C A C h x = = = i i i i i j i j N A h x P N A h x = = = 每个小球落入第i个狭槽的概率,为 这就是说,小球在某处出 现的概率是和该处的高度 成正比的。 要对小球沿x 的分布作更细致的描述, 我们可以一步步地把狭槽 的宽度减小、数目加多, 如图 (b)、(c)所示
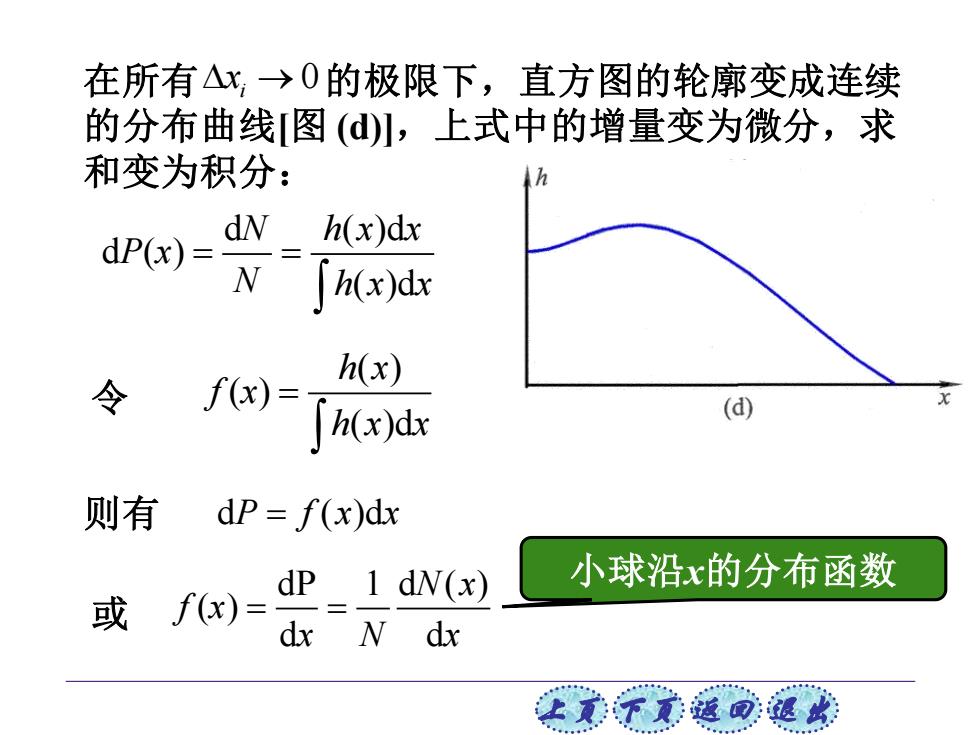
在所有△x,→0的极限下,直方图的轮廓变成连续 的分布曲线[图()川,上式中的增量变为微分,求 和变为积分: dP(x)= dN h(x)dx h(x)dx h(x) 令 f(x)= [h(x)dx (d) 则有 dP=f(x)dx dP 1 dN(x) 小球沿x的分布函数 或fx)= dx dx 让美下觉返司速此
上页 下页 返回 退出 在所有 的极限下,直方图的轮廓变成连续 的分布曲线[图 (d)],上式中的增量变为微分,求 和变为积分: 0 i →x d ( )d d ( ) ( )d N h x x P x N h x x = = 令 ( ) ( ) ( )d h x f x h x x = 则有 d ( )d P f x x = 或 dP 1 d ( ) ( ) d d N x f x x N x = = 小球沿x的分布函数

换句话来说,就是小球落在x附近dx区间的概率dP 正比于区间的大小dx,分布函数fx)代表小球落入x 附近单位区间的概率dPx)(dx),或者说,fx)是小 球落在x处的概率密度。 由此可知有 归一化条件 为了突出小球按狭槽位置x分布的情况,考虑到小 球在槽中的积累高度代表的其实就是小球在此出 现的概率,可用fx)代替h。 对某一个任意选定的球来说,x)dx也可理解为球 的位置在x与x+dx之间的概率
上页 下页 返回 退出 换句话来说,就是小球落在x附近dx区间的概率dP 正比于区间的大小dx,分布函数f(x)代表小球落入x 附近单位区间的概率dP(x)/(dx),或者说,f(x)是小 球落在x处的概率密度。 由此可知有 d ( ) ( )d 1 N x f x x N = = 归一化条件 为了突出小球按狭槽位置x分布的情况,考虑到小 球在槽中的积累高度h代表的其实就是小球在此出 现的概率,可用f(x)代替h。 对某一个任意选定的球来说,f(x)dx也可理解为球 的位置在x与x+dx之间的概率