
*§5-6麦克斯韦一玻耳兹曼能量分布律 重力场中粒子按高度分布 一、麦克斯韦一玻耳兹曼分布律 玻耳兹曼把麦克斯韦速率分布律推广到气体分 子在任意力场中运动的情形 当气体处于平衡状态时,在一定温度下,在速度 分布间隔 yx~Vx+△yx;yy~,+△yy;V:~y+△y 和坐标分布间隔 x~x+△x;y~y+△y;Z~Z+△z 让美子元返司退
上页 下页 返回 退出 一、 麦克斯韦—玻耳兹曼分布律 玻耳兹曼把麦克斯韦速率分布律推广到气体分 子在任意力场中运动的情形 。 当气体处于平衡状态时,在一定温度下,在速度 分布间隔 和坐标分布间隔 *§5-6 麦克斯韦—玻耳兹曼能量分布律 重力场中粒子按高度分布 ~ ; x x x v v v + ~ ; y y y v v v + v v v z z z ~ + x x x ~ ; + y y y ~ ; + z z z ~ +

内的分子数为 AN'=no m,e(+B,/r△y,△y,Ay.AYAYA 2πkT 麦克斯韦一玻耳兹曼分布律 式中Ek代表动能,E,代表势能,no代表在E。=0处单 位体积内具有各种速度值的总分子数
上页 下页 返回 退出 内的分子数为 3 2 k p ( )/ 0 0 ' ( ) e 2π E E kT x y z m N n v v v x y z kT − + = 麦克斯韦—玻耳兹曼分布律 式中Ek代表动能, Ep代表势能, n0代表在 Ep=0处单 位体积内具有各种速度值的总分子数

注意: ()在相同的速度间隔和空间间隔,分子数的多少取 决于分子能量E的大小,分子能量愈大,分子数愈少, 这表明,就统计的意义而言,气体分子将占据能量 较低的状态。 (2)玻耳兹曼分布律对实物微粒(气体分子、液体分子、 固体分子、布朗粒子等)在不同力场中运动的情形都 是成立的。 为eE+,/Ay,△y,Ay.AxAA正 AN'=no 3)将上式对速度积分,并考虑到分布函数的归一化, 则玻耳兹曼分布率也可以写成如下形式: △NB=n,e△x△yAE 让美觉返司退
上页 下页 返回 退出 注意: (1)在相同的速度间隔和空间间隔,分子数的多少取 决于分子能量E的大小,分子能量愈大,分子数愈少, 这表明,就统计的意义而言,气体分子将占据能量 较低的状态。 (2) 玻耳兹曼分布律对实物微粒(气体分子、液体分子、 固体分子、布朗粒子等)在不同力场中运动的情形都 是成立的 。 (3)将上式对速度积分,并考虑到分布函数的归一化, 则玻耳兹曼分布率也可以写成如下形式: 3 2 k p ( )/ 0 0 ' ( ) e 2π E E kT x y z m N n v v v x y z kT − + = p / B 0e E kT N n x y z − =

二、重力场中粒子按高度的分布 在重力场中,气体分子受到两种互相对立的作 用。无规则的热运动将使气体分子均匀分布于它们 所能到达的空间,而重力则要使气体分子聚拢在地 面上,当这两种作用达到平衡时,气体分子在空间 作非均匀的分布,分子数随高度减小。 设=0处势能为零,则分布在高度为z处的体 积元△V=△x△y△z内的分子数为 mogz △NB=nekr△x△y△z 让美不美返回退块
上页 下页 返回 退出 二、 重力场中粒子按高度的分布 在重力场中,气体分子受到两种互相对立的作 用。无规则的热运动将使气体分子均匀分布于它们 所能到达的空间,而重力则要使气体分子聚拢在地 面上,当这两种作用达到平衡时,气体分子在空间 作非均匀的分布,分子数随高度减小。 设z=0处势能为零,则分布在高度为z处的体 积元V= x y z内的分子数为 0 B 0e m gz N n x y z kT − =
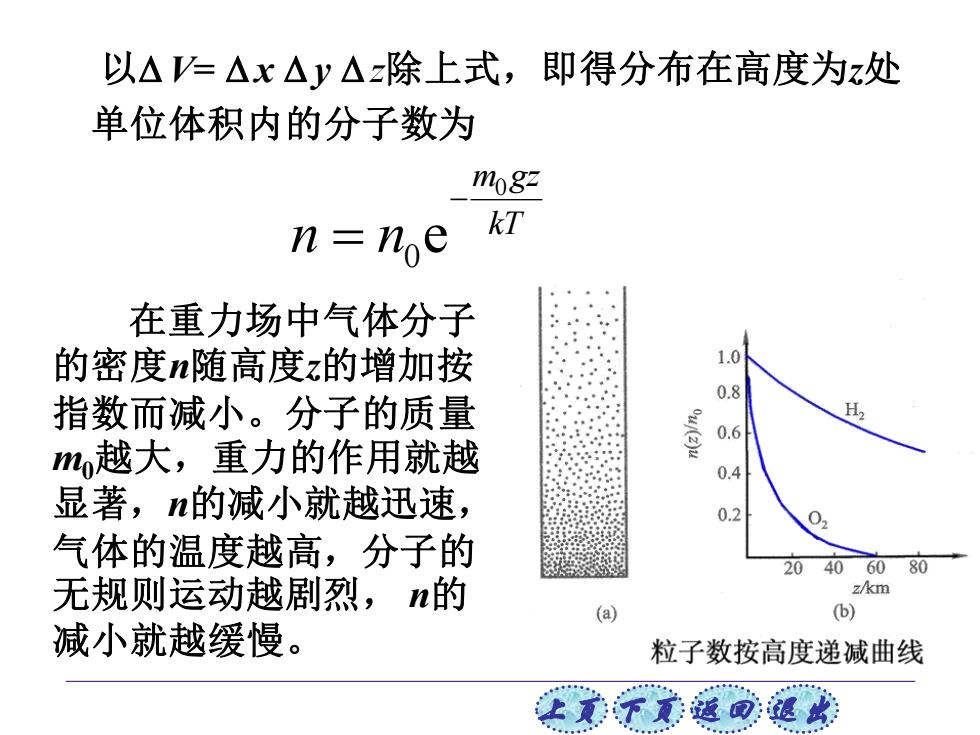
以△=△x△y△除上式,即得分布在高度为z处 单位体积内的分子数为 1m08z n=ne kT 在重力场中气体分子 的密度n随高度z的增加按 1.0 0 指数而减小。分子的质量 0.6 H m越大,重力的作用就越 0.4 显著,n的减小就越迅速, 03 气体的温度越高,分子的 204060 80 无规则运动越剧烈,n的 z/km (a) (b) 减小就越缓慢。 粒子数按高度递减曲线 王觉下元菠面:退收
上页 下页 返回 退出 在重力场中气体分子 的密度n随高度z的增加按 指数而减小。分子的质量 m0越大,重力的作用就越 显著,n的减小就越迅速, 气体的温度越高,分子的 无规则运动越剧烈, n的 减小就越缓慢。 0 0 e m gz kT n n − = 以 V= x y z除上式,即得分布在高度为z处 单位体积内的分子数为

又据 p=nkT 将分子数密度代入,得 气压公 mogz 式 Mmolg= p=poe kT Poe RT 设=0处分子数密度为p0,重力场中气体的压强随 高度的增加按指数规律减小。 设温度不随高度变化. 根据压强变化测高度,实际温度也随高度变化,测 大气温度有一定的范围,是近似测量。 RT 高度 由上式可得高度为 gM mol 王意了元返回退
上页 下页 返回 退出 0 mol 0 0 e e m gz M gz kT RT p p p − − = = 将分子数密度代入,得 设z=0处分子数密度为p0 , 重力场中气体的压强随 高度的增加按指数规律减小。 气压公 式 设温度不随高度变化. 根据压强变化测高度,实际温度也随高度变化,测 大气温度有一定的范围,是近似测量。 由上式可得高度 z为 0 mol ln RT p z gM p = 高度 计 又据 p nkT =

选择进入下一节 §50教学基本要求 §5-1热运动的描述理想气体模型和物态方程 §5-2分子热运动和统计规律 §5-3理想气体的压强和温度公式 §5-4能量均分定理理想气体的内能 §5-5麦克斯韦速率分布律 *§5-6麦克斯韦-玻耳兹曼能量分布律重力场中粒 子按高度的分布 §5-7分子碰撞和平均自由程 *§5-8气体的输运现象 *§59真实气体范德瓦尔斯方程 觉子觉道司退欢
上页 下页 返回 退出 选择进入下一节 §5-0 教学基本要求 §5-1 热运动的描述 理想气体模型和物态方程 §5-2 分子热运动和统计规律 §5-3 理想气体的压强和温度公式 §5-4 能量均分定理 理想气体的内能 §5-5 麦克斯韦速率分布律 *§5-6 麦克斯韦-玻耳兹曼能量分布律 重力场中粒 子按高度的分布 §5-7 分子碰撞和平均自由程 *§5-8 气体的输运现象 *§5-9 真实气体 范德瓦尔斯方程