§5-9真实气体 范德瓦尔斯方程 一、真实气体等温线 理想气体 忽略分子的体积与分子间的引力 实际气体 温度不太低 压强不太高 理想气体 让美觉返司退
上页 下页 返回 退出 理想气体 实际气体 温度不太低 压强不太高 忽略分子的体积与分子间的引力 理想气体 *§ 5-9 真实气体 范德瓦尔斯方程 一、 真实气体等温线
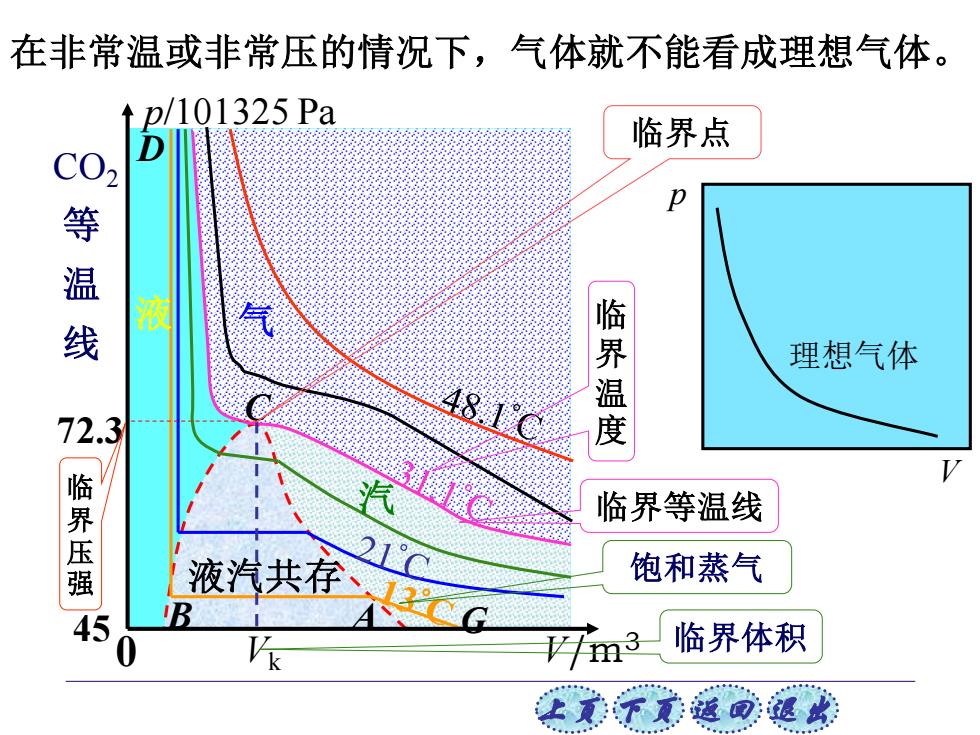
在非常温或非常压的情况下,气体就不能看成理想气体。 p/101325Pa 临界点 p 等温线 液 理想气体 72.3 48.1C 临界温度 临界压强 临界等温线 液汽共c 21C 饱和蒸气 45 a3, 临界体积 女意子意适司退此
上页 下页 返回 退出 V/m3 C Vk 72.3 450 气 液汽共存 液 p/101325 Pa B A D G 汽 CO2 等 温 线 临 界 压 强 临界等温线 临 界 温 度 临界点 临界体积 饱和蒸气 在非常温或非常压的情况下,气体就不能看成理想气体。 理想气体 p V

真实气体的等温线可以分成四个区域: 汽态区(能液化),液汽共存区,液态区,气态区 (不能液化)。 饱和蒸气压(汽液共存时的压强)与体积无关。 临界点以下汽体可等温压缩液化,以上气 体不能等温压缩液化。 在临界等温曲线的拐点处的温度、压强、 体积分别称为临界温度T、临界压强P和 临界体积Vk。 让美下觉返同速
上页 下页 返回 退出 饱和蒸气压(汽液共存时的压强)与体积无关。 临界点以下汽体可等温压缩液化,以上气 体不能等温压缩液化。 真实气体的等温线可以分成四个区域: 汽态区(能液化),液汽共存区,液态区,气态区 (不能液化)。 在临界等温曲线的拐点处的温度、压强、 体积分别称为临界温度 、临界压强 和 临界体积 。 Tk pk Vk
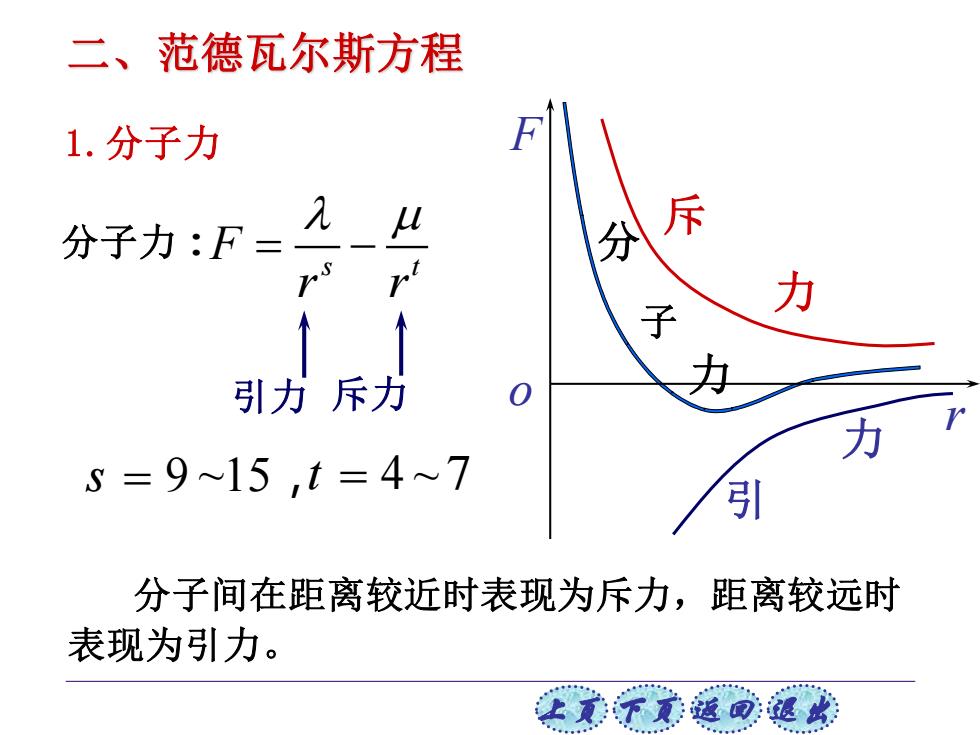
二、范德瓦尔斯方程 1.分子力 分子力:F= A u 分斥 力 引力斥力 力 5=9~15,t=4~7 引 分子间在距离较近时表现为斥力,距离较远时 表现为引力
上页 下页 返回 退出 分子力: s = 9 ~15,t = 4 ~7 引力 斥力 力 分 子 斥 力 引 力 r F o 分子间在距离较近时表现为斥力,距离较远时 表现为引力。 s t F r r = − 1.分子力 二、范德瓦尔斯方程

2.对体积的修正 1mol理想气体的状态方程可写成 pV =RT 每个分子可以自由活动的空间体积。理想 m 气体,分子无大小,故它也是容器的体积。 p 实际测量值。 分子有大小时,则每个分子活动的自由空间必 然小于V,因此可从Vm中减去一个反映分子咱占 有体积的修正量b,状态方程改写为 p(Vin -b)=RT 让美下元返回:退欢
上页 下页 返回 退出 1mol 理想气体的状态方程可写成 m pV RT = 分子有大小时,则每个分子活动的自由空间必 然小于Vm,因此可从Vm 中减去一个反映分子咱占 有体积的修正量b,状态方程改写为 2.对体积的修正 ——每个分子可以自由活动的空间体积。理想 气体,分子无大小,故它也是容器的体积。 Vm p ——实际测量值。 m p V b RT ( ) − =

修正量b的确定 4 一对分子空间体积为 nd3 3 1mol气体分子的空间体积为 b=水号d}4战青2学 刚性球 d =4倍分子本身体积之和 1mol理想气体物态方程 RT pVm=RT→ P= V-b 完成了第一步的修正。 让贰不美返回退此
上页 下页 返回 退出 d B A 刚性球 d 1mol 气体分子的空间体积为 = 4倍分子本身体积之和 一对分子空间体积为 3 π 3 4 d 3 3 0 0 4 1 4 π 4 π( ) 3 2 3 2 d b N d N = = 修正量b的确定 m RT p V b = m − pV RT = 1mol理想气体物态方程 完成了第一步的修正
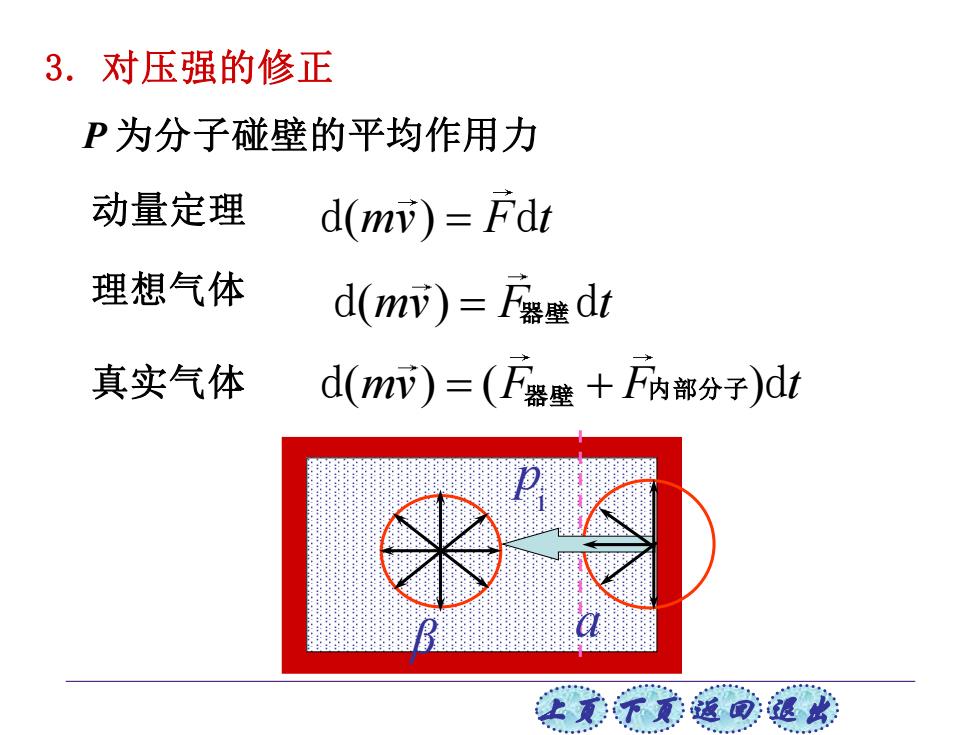
3.对压强的修正 P为分子碰壁的平均作用力 动量定理 d(mv)=Fdt 理想气体 d(m)=F器壁dt 真实气体 d()=(F器壁+F内部分子)dt 让式下式返回退
上页 下页 返回 退出 3. 对压强的修正 理想气体 P 为分子碰壁的平均作用力 动量定理 d d ( ) mv F t = 真实气体 β p i a d d ( ) ( ) mv F F t = + 器壁 内部分子 d d ( ) mv F t = 器壁

RT 修正为p= y-6 由于分子之间存在引力而造成对器壁压强减少 内压强 Pi 基本完成了第二步的修正 内压强 1)与碰壁的分子数成正比 2)与对碰壁分子有吸引力作用的分子数成正比 p:ocn.n=n 1 a 即 写成 P:= m m
上页 下页 返回 退出 i m RT p p V b = − − 修正为 内压强 pi 基本完成了第二步的修正 由于分子之间存在引力而造成对器壁压强减少 内压强 1) 与碰壁的分子数成正比 2) 与对碰壁分子有吸引力作用的分子数成正比 2 i p n n n = i 2 m 1 p V i 2 m a p V 即 写成 =

m ☑与分子的种类有关,需实际测量 1mol范德瓦尔斯气体状态方程为 p+ a (Vm-b)=RT 和b是与分子有关的修正因子,需查表。 m 对质量为m任何实际气体:V= m m p+ b)= m RT Mmel 让美觉返司退
上页 下页 返回 退出 a 与分子的种类有关,需实际测量 1mol范德瓦尔斯气体状态方程为 ( m ) 2 m a p V b RT V + − = a和b是与分子有关的修正因子, 需查表。 i 2 m a p V = 对质量为m 任何实际气体: 2 2 2 mol mol mol ( )( ) m a m m p V b RT M V M M + − = m mol m V V M =
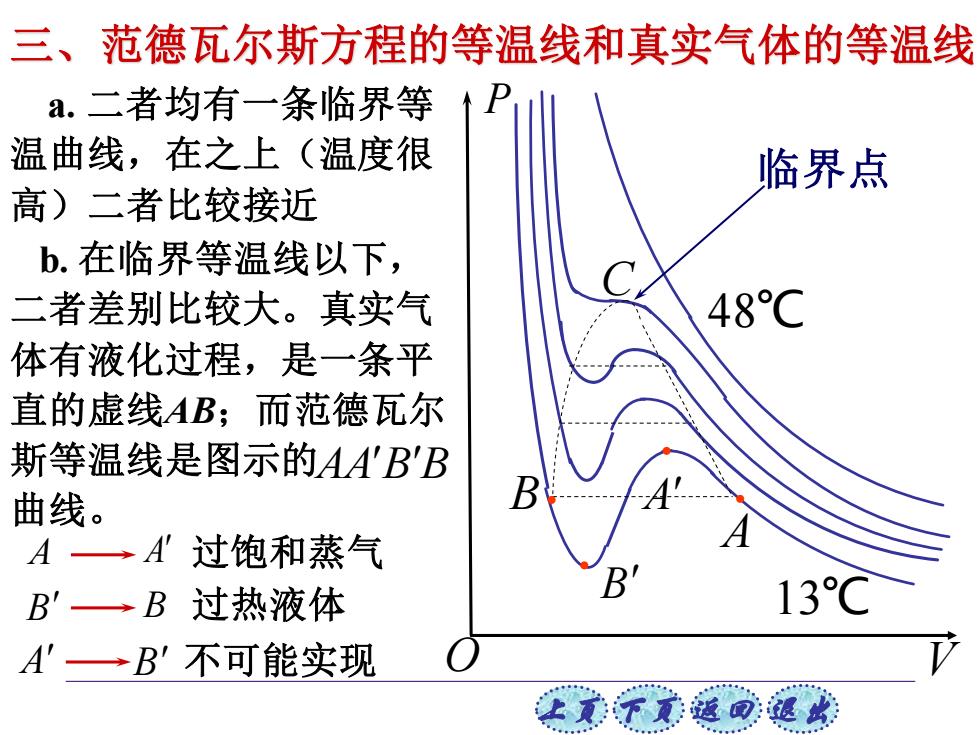
三、范德瓦尔斯方程的等温线和真实气体的等温线 a.二者均有一条临界等 温曲线,在之上(温度很 临界点 高)二者比较接近 b.在临界等温线以下, 二者差别比较大。真实气 48℃ 体有液化过程,是一条平 直的虚线AB;而范德瓦尔 斯等温线是图示的AA'B'B 曲线。 B A→A'过饱和蒸气 B'→B过热液体 13C A'一B'不可能实现 让美子意适可退此
上页 下页 返回 退出 三、范德瓦尔斯方程的等温线和真实气体的等温线 a. 二者均有一条临界等 温曲线,在之上(温度很 高)二者比较接近 过饱和蒸气 过热液体 不可能实现 b. 在临界等温线以下, 二者差别比较大。真实气 体有液化过程,是一条平 直的虚线AB;而范德瓦尔 斯等温线是图示的 曲线。 AA B B A A B B A B V 48℃ 13℃ C P O 临界点 A A . . B B.