《普通物理学》课程教学资源（PPT课件）第七章 静止电荷的电场 7-9 有电介质时的高斯定理、电位移

§7-9有电介质时的高斯定理电位移 一、有电介质时的高斯定理 电位移 在有电介质存在的电场中，高斯定理仍成立，但要 同时考虑自由电荷和束缚电荷产生的电场。 自由电荷 总电场 fE.ds=1(亿9+∑q 极化电荷 60 上式中由于极化电荷一般也是未知的，用其求解电 场问题很困难，为便于求解，引入电位移矢量，使 右端只包含自由电荷

上页 下页 返回 退出 §7-9 有电介质时的高斯定理 电位移 一、有电介质时的高斯定理 电位移 在有电介质存在的电场中，高斯定理仍成立，但要 同时考虑自由电荷和束缚电荷产生的电场。 总电场 极化电荷 自由电荷 上式中由于极化电荷一般也是未知的，用其求解电 场问题很困难，为便于求解，引入电位移矢量，使 右端只包含自由电荷。 (  )  E  S = q + q  S 0 0 1 d   

设无限大平行板间充满均匀电介质，两极板所带自 由电荷面密度为±o。,电介质极化后两表面极化电 荷面密度为±σ'。 取圆柱形高斯面如图中虚线 +土土土 所示，则 EdS=(GoS,+as:) fp.ds=八p.ds+八pd 由于S1在导体中，P=0又o'=P fp.ds=jip.ds =PS2 ='S 让美觉返司退

上页 下页 返回 退出 + + + + + + + + + + + + + + + + + + + + - - - - - - - - - - - - - - - - - - E  P  + 0 + − − 0 S1 2 S 设无限大平行板间充满均匀电介质，两极板所带自 由电荷面密度为 ，电介质极化后两表面极化电 荷面密度为 。  0  取圆柱形高斯面如图中虚线 所示，则 又 P  由于S1在导体中， P = 0  =  PS2  S2 = =  ( ) 0 1 2 0 1 E dS S S S     = +         =  +  1 2 d d d S S S P S P S P S          =  2 d d S S P S P S    

E.d5-1ous,-If.ds 60 令9o=OS1代入上式并移项，得 f乐，(E+P5=9 定义：电位移矢量 D=8E+P 则可得有电介质 时的高斯定理 D.ds=9g。 电位移线的描画方法同电场线的描画。垂直于电位 移线单位面积上通过的电位移线数目等于该点电位 移的量值，称为电通量

上页 下页 返回 退出 令 q0 = 0 S1 代入上式并移项，得 定义：电位移矢量 D E P    =  0 + 则可得有电介质 时的高斯定理 电位移线的描画方法同电场线的描画。垂直于电位 移线单位面积上通过的电位移线数目等于该点电位 移的量值，称为电通量。    = −  S S E S S P S     d 1 1 d 0 0 1 0    ( ) 0 E P dS q0 S +  =      D dS q0 S  =   

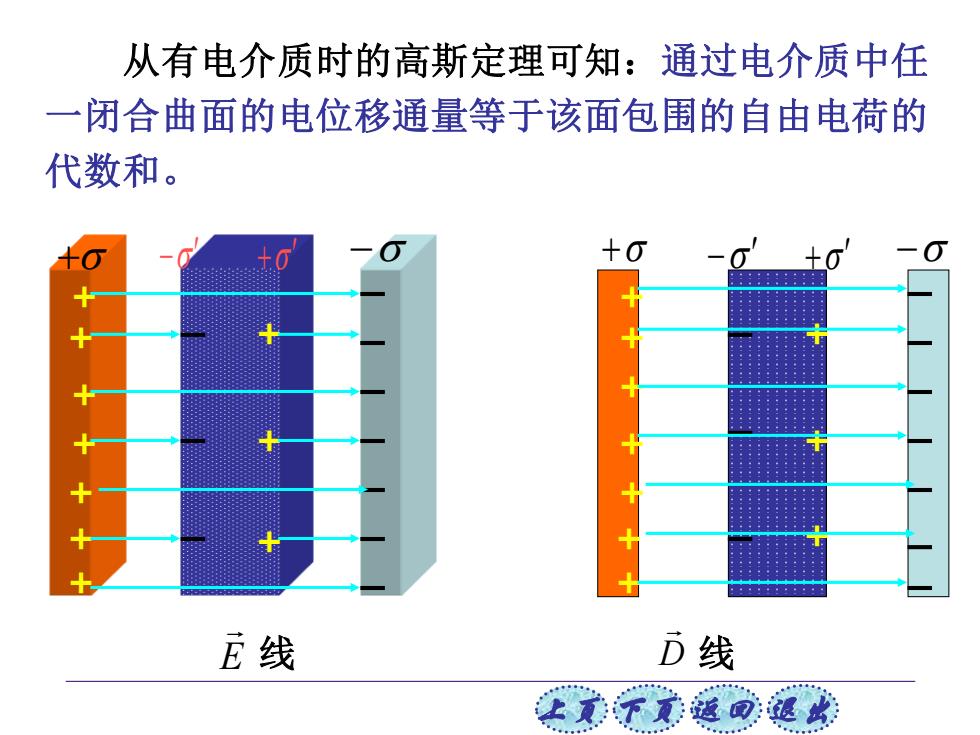
从有电介质时的高斯定理可知：通过电介质中任 一闭合曲面的电位移通量等于该面包围的自由电荷的 代数和。 E线 D线 让文不美蕴回蕴以

上页 下页 返回 退出 + + + + + + + − + − + + + + + + + + + + + − + − + + + + 线 D 线  E  从有电介质时的高斯定理可知：通过电介质中任 一闭合曲面的电位移通量等于该面包围的自由电荷的 代数和

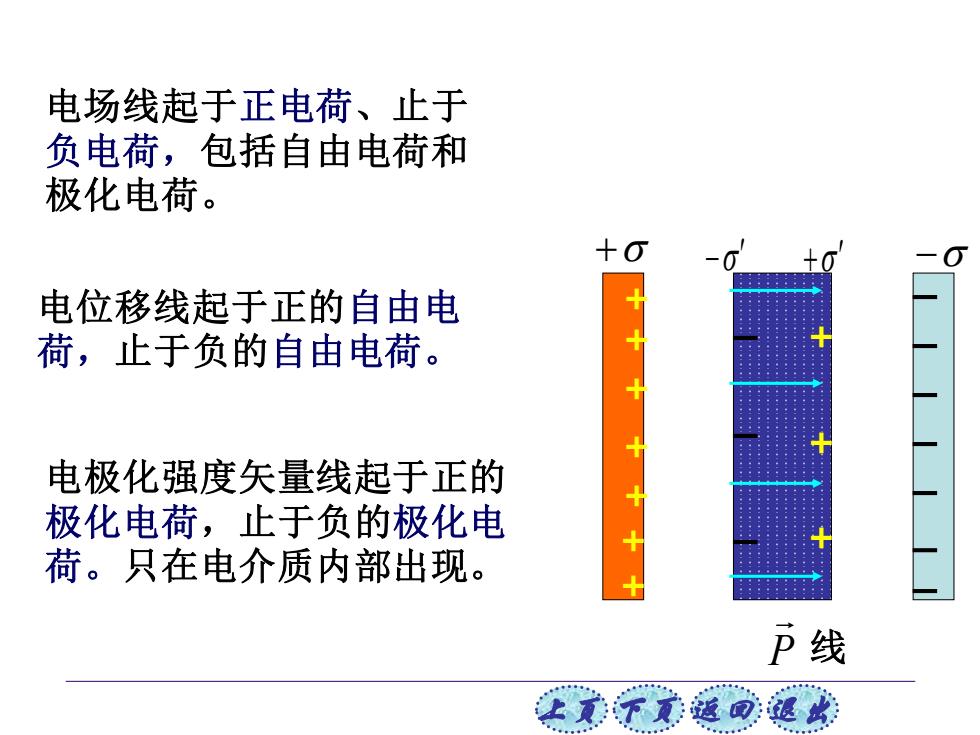
电场线起于正电荷、止于 负电荷，包括自由电荷和 极化电荷。 电位移线起于正的自由电 荷，止于负的自由电荷。 电极化强度矢量线起于正的 极化电荷，止于负的极化电 荷。只在电介质内部出现。 P线 意子元道回退瑞

上页 下页 返回 退出 + − + − + + + + + + + + + + P 线  电位移线起于正的自由电 荷，止于负的自由电荷。 电场线起于正电荷、止于 负电荷，包括自由电荷和 极化电荷。 电极化强度矢量线起于正的 极化电荷，止于负的极化电 荷。只在电介质内部出现

二、D、E、P三矢量之间关系 85R}n0-cE p=,(e.-1)E 有电介质存在时的高斯定理的应用 (1)分析自由电荷分布的对称性，选择适当的高斯面 求出电位移矢量。 (2)根据电位移矢量与电场的关系，求出电场。 (3)根据电极化强度与电场的关系，求出电极化强度。 (4)根据束缚电荷与电极化强度关系，求出束缚电荷。 让美觉返司退

上页 下页 返回 退出 D E P    =  0 + P E   ( 1) =  0  r − D E E    =   =  0 r 有电介质存在时的高斯定理的应用 （1）分析自由电荷分布的对称性，选择适当的高斯面 求出电位移矢量。 （2）根据电位移矢量与电场的关系，求出电场。 （3）根据电极化强度与电场的关系，求出电极化强度。 （4）根据束缚电荷与电极化强度关系，求出束缚电荷。 二、 D E P 三矢量之间关系    、

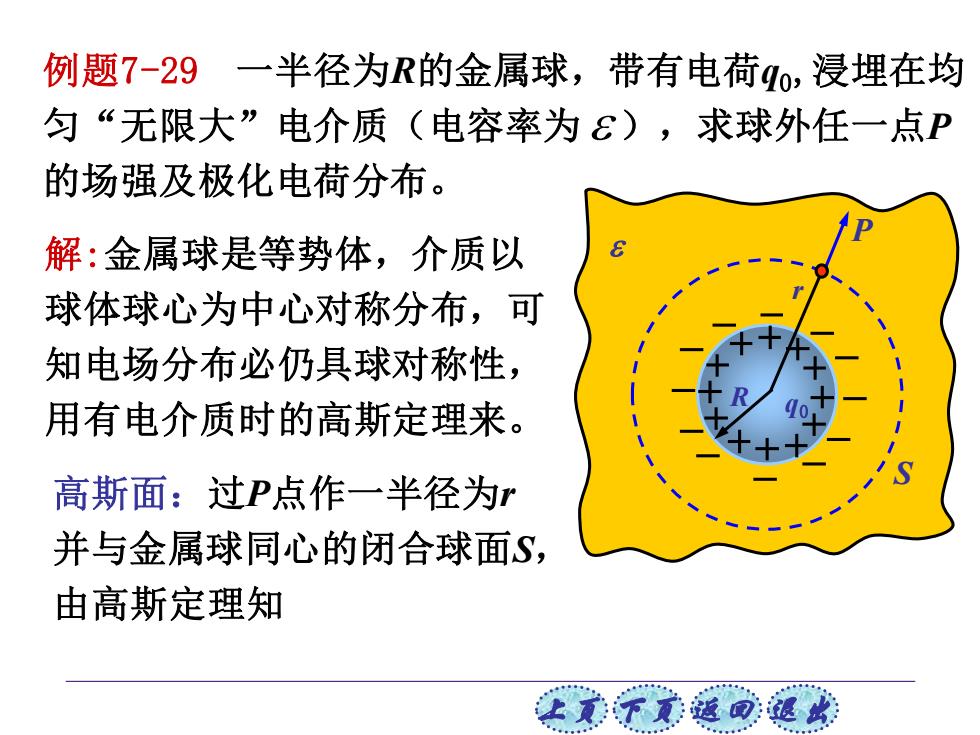
例题7-29一半径为R的金属球，带有电荷q0,浸埋在均 匀“无限大”电介质（电容率为E),求球外任一点P 的场强及极化电荷分布。 解：金属球是等势体，介质以 球体球心为中心对称分布，可 知电场分布必仍具球对称性， 用有电介质时的高斯定理来。 高斯面：过P点作一半径为 并与金属球同心的闭合球面S, 由高斯定理知 上贰不觉返回退此

上页 下页 返回 退出 例题7-29 一半径为R的金属球，带有电荷q0,浸埋在均 匀“无限大”电介质（电容率为 ），求球外任一点P 的场强及极化电荷分布。 解:金属球是等势体，介质以 球体球心为中心对称分布，可 知电场分布必仍具球对称性， 用有电介质时的高斯定理来。 R q0 r P S  高斯面：过P点作一半径为r 并与金属球同心的闭合球面S， 由高斯定理知 

f月D.d5=D4r2=g。 所以 D 4r2 写成矢量式为D= 因D=E,所以离球心r处P点的场强为 龙= D 90 ATEr?er ATEner?e 0 让美下觉返同速

上页 下页 返回 退出 2 0 4πr q D = 0 2 4π r q D e r = 所以 写成矢量式为 0 2 DdS =D4πr = q    D E   因 =  , 所以离球心r 处P点的场强为 0 0 0 2 2 0 r 0 4π 4π r r D q q E E e e r r = = = =     

结果表明：带电金属球周围充满均匀无限大电介 质后，其场强减弱到真空时的1/ε倍，可求出电极化 强度为 P= 42 电极化强度p与有关，是非均匀极化。在电介 质内部极化电荷体密度等于零，极化面电荷分布 在与金属交界处的电介质表面上（另一电介质表 面在无限远处)，其电荷面密度为 o'=p.e。 让无子文返回退此

上页 下页 返回 退出 0 0 0 r 2 2 2 0 0 r r 1 4π 4π 4π r r r q q q P e e e r r r   − = − =          结果表明：带电金属球周围充满均匀无限大电介 质后，其场强减弱到真空时的 倍, 可求出电极化 强度为 电极化强度 与 有关，是非均匀极化。在电介 质内部极化电荷体密度等于零，极化面电荷分布 在与金属交界处的电介质表面上（另一电介质表 面在无限远处），其电荷面密度为 P  r  n P e    =  1 r 

三一 9 4πR2 因为8.>1，上式说明。恒与q0反号，在交界面 处自由电荷和极化电荷的总电荷量为 go- 总电荷量减小到自由电荷量的1/ε.倍，这是离球 心r处P点的场强减小到真空时的/ε倍的原因。 让美下文返面退

上页 下页 返回 退出         −  = − r r 2 0 1 4π    R q r 0 0 r r 0 1    q q q =         − − 因为 >1，上式说明 恒与q0反号，在交界面 处自由电荷和极化电荷的总电荷量为 总电荷量减小到自由电荷量的 倍，这是离球 心r处P点的场强减小到真空时的 倍的原因。  1 r  1 r  r 