
§10-1谐振动 一、简谐振动的特征及其表达式 简谐振动:物体运动时,离开平衡位置的位移 (或角位移)按余弦(或正弦)规律随时间变化。 让美子意适可退
上页 下页 返回 退出 简谐振动:物体运动时,离开平衡位置的位移 (或角位移)按余弦(或正弦)规律随时间变化。 一、简谐振动的特征及其表达式 §10-1 谐振动
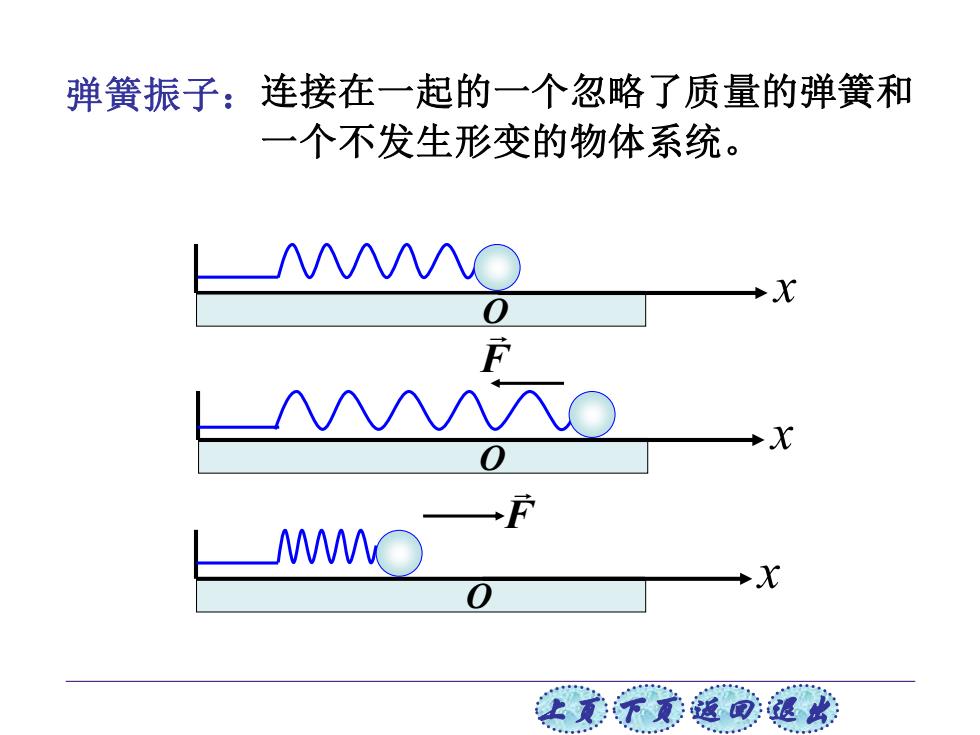
弹簧振子:连接在一起的一个忽略了质量的弹簧和 一个不发生形变的物体系统。 ○ -X C 让美觉返司退
上页 下页 返回 退出 连接在一起的一个忽略了质量的弹簧和 一个不发生形变的物体系统。 弹簧振子: x O F F x O x O

回复力:作简谐运动的质点所受的沿位移方向的合 外力,该力与位移成正比且反向。 简谐振动的动力学特征:F=一kx F k 据牛顿第二定律,得A=一=-一x,令 k=02 m m m d2x a= =-02x一运动学特征 位移x之解可写为 x=AcoS(ot+中,) 或X=Aei(or+) 让贰下觉返回退
上页 下页 返回 退出 回复力:作简谐运动的质点所受的沿位移方向的合 外力, 该力与位移成正比且反向。 简谐振动的动力学特征: 据牛顿第二定律,得 运动学特征 位移 x 之解可写为 F = −kxx, m k m F a = = − 令 k 2 m = x t x a 2 2 2 d d = = − 或 0 i( ) e t x A + x A t = + cos( ) 0 =

用旋转矢量图画简谐运动的x一t图 x =Acos(@t+p) X ↑A A p=0 p=π/2 让美下觉返同速
上页 下页 返回 退出 用旋转矢量图画简谐运动的 x −t 图

简谐振动的运动学特征: 物体的加速度与位移成正比而方向相反,物 体的位移按余弦规律变化。 dx 速度 V= =-oA sin(ot+中) dt 加速度 a= x=-02Acos(of+4) dt2 让意不意道可退欢
上页 下页 返回 退出 简谐振动的运动学特征: 物体的加速度与位移成正比而方向相反,物 体的位移按余弦规律变化。 速度 加速度 sin( ) d d = = − +0 A t t x v cos( ) d d 0 2 2 2 = = − A t + t x a
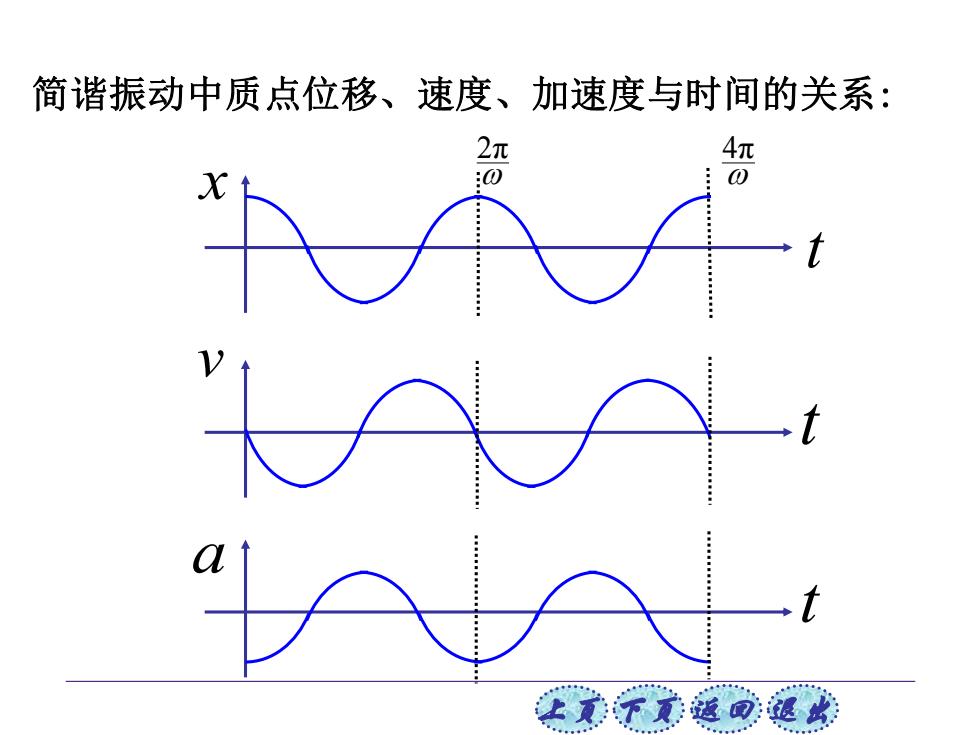
简谐振动中质点位移、速度、加速度与时间的关系: 2元 4元 :0 让式下式返回退
上页 下页 返回 退出 简谐振动中质点位移、速度、加速度与时间的关系: 4π 2π x t v t t a

○常量和的确定 根据初始条件:=0时,x=x,V=V,得 xo =Acos,vo =-@Asin A=Vx好+(,/o)2 0X0 在一元到十元之间,通常中。存在两个值,可根据 V,=-@Asin4进行取舍。 让意了意适回退块
上页 下页 返回 退出 常量 A 和 0 的确定 根据初始条件: t=0 时, x=x0 , v v = 0 ,得 0 0 0 0 x = Acos , v = −Asin 2 0 2 0 A = x + (v ) 0 0 0 arctan v x = − 在 −π 到 +π 之间,通常 0 存在两个值,可根据 0 0 v A = − sin 进行取舍

二、描述谐振动的特征量 1.振幅:物体离开平衡位置的最大位移的绝对值。 A=Vx+(/o)2 一由初始条件确定 2周期和频率 周期:物体作一次完全振动所经历的时间。 x=Acos(ot+)=Acos[@(T+)+ Ts2π 0 频率:单位时间内物体所作完全振动的次数。 0 V= T 2元 让美觉返司退
上页 下页 返回 退出 1.振幅: 物体离开平衡位置的最大位移的绝对值。 由初始条件确定 2 周期和频率 周期:物体作一次完全振动所经历的时间。 频率:单位时间内物体所作完全振动的次数。 二、描述谐振动的特征量 2 0 2 0 A = x + (v ) 0 0 x A t A T t = + = + + cos( ) cos[ ( ) ] 2π T = 1 T 2π = =

角频率:物体在2π秒内所作的完全振动的次数。 2元 0= =2iV 对于弹簧振子,因有o=√k/m,得 m k 7=2v=2 利用上述关系式,得谐振动表达式: x=Acos(2πVt+4) 让美不意返回退
上页 下页 返回 退出 角频率: 物体在 2π 秒内所作的完全振动的次数。 利用上述关系式,得谐振动表达式: 2π 2π T = = 对于弹簧振子,因有 = k m ,得 2π , 2π m k T k m = = 0 2π x A t cos T = + 0 x A t = + cos(2π )

3.相位和初相 相位(⊙t+,铁定简谐运动状态的物理量。 初相位中。:=0时的相位。 相位概念可用于比较两个谐振动之间在振动步 调上的差异。 设有两个同频率的谐振动,表达式分别为 x=A4 cos(at+o) x2=4 cos(at+0) 让美下觉返同速
上页 下页 返回 退出 3.相位和初相 相位 ( :决定简谐运动状态的物理量。 ) +0 t 初相位 0 :t=0 时的相位。 相位概念可用于比较两个谐振动之间在振动步 调上的差异。 设有两个同频率的谐振动,表达式分别为 cos( ) 1 = 1 +10 x A t cos( ) 2 = 2 +20 x A t