§11-2平面简谐波的波函数 一、 波函数 用数学函数式表示介质中质点的振动状态随时 间变化的关系:5(r,t)=f(r,t)=f(x,y,2,t) 二、平面简谐波的波函数 平面简谐波: 波面为平面的简谐波. 平面简谐波传播时,介质中各质点都作同频率的简 谐波动,在任一时刻,各点的振动相位一般不同,它们 的位移也不相同。据波阵面的定义可知,任一时刻在同 一波阵面上的各点有相同的相位,它们离开各自的平衡 位置有相同的位移。 让美下元返回退欢
上页 下页 返回 退出 §11-2 平面简谐波的波函数 一、波函数 用数学函数式表示介质中质点的振动状态随时 间变化的关系: ( ) ( ) ( ) r t f r t f x y z t , = = , , 二、平面简谐波的波函数 平面简谐波: 波面为平面的简谐波. x y 平面简谐波传播时,介质中各质点都作同一频率的简 谐波动,在任一时刻,各点的振动相位一般不同,它们 的位移也不相同。据波阵面的定义可知,任一时刻在同 一波阵面上的各点有相同的相位,它们离开各自的平衡 位置有相同的位移
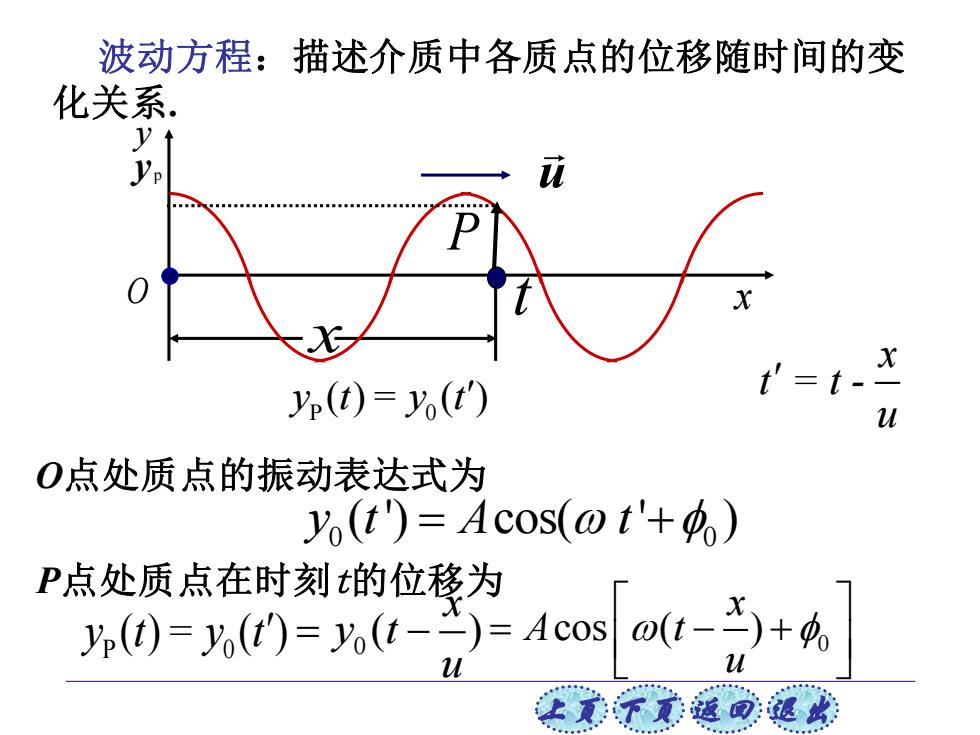
波动方程:描述介质中各质点的位移随时间的变 化关系. y↑ yp(t)=yo(t) O点处质点的振动表达式为 yo(t)=Acos(@t+) P点处质点在时刻的位移为 ()=(t)=,(t-)=Acos ot-)+
上页 下页 返回 退出 y x x P O t y p P 0 y t = y t ( ) ( ) u O点处质点的振动表达式为 0 0 y t A t ( ') cos( ' ) = + x t = t - u P 0 y t = y t ( ) ( ) P点处质点在时刻t的位移为 波动方程:描述介质中各质点的位移随时间的变 化关系. 0 ( ) x y t u = − 0 cos ( ) x A t u = − +

P点处质点在时刻的位移为: w0=slav-5台 波函数 因此,波线上任一点在任一时刻的位移 都能由上式给出。此即所求的沿x轴正方向 前进的平面简谐波的波函数。 沿x轴负方向传播的平面简谐波的波函数 让美下元返回:退欢
上页 下页 返回 退出 P点处质点在时刻t 的位移为: 因此,波线上任一点在任一时刻的位移 都能由上式给出。此即所求的沿x轴正方向 前进的平面简谐波的波函数。 波 函 数 沿x轴负方向传播的平面简谐波的波函数 p 0 ( ) cos ( ) x y t A t u = − +
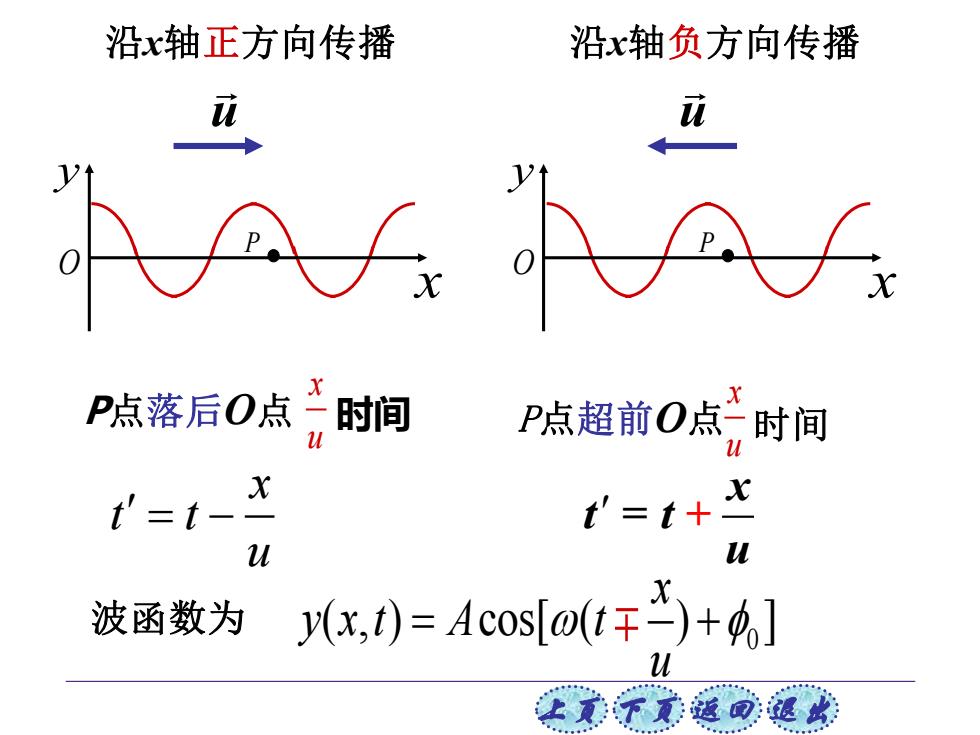
沿x轴正方向传播 沿x轴负方向传播 0 P点落后O点二时间 P点超前O点二时间 X t'=t- t'=t+ u 波函数为 x,t0=Acos(年)+4,] W
上页 下页 返回 退出 u u 沿x轴正方向传播 沿x轴负方向传播 P点落后O点 x u x u P点超前O点 O x y P O x y P t = t + x u 时间 时间 波函数为 0 ( , ) cos[ ( ) ] x y x t A t u = + x t t u = −

利用关系式0=2=2元v和T=入,得 波函数其他形式 y=Acos 2(宁克+ y=Acos 2 2xw年克+% y=Ac0s(ot干ar+4),k=2π 角波数 y=AcOs(ot干 +) 2元x =eao的 让美觉返司退
上页 下页 返回 退出 波函数其他形式 0 cos 2π( ) t x y A T = + 0 cos 2π( ) x y A t = + 0 y A t kx = + cos( ), 0 2π cos( ) x y A t = + 角波数 2π k = 0 ( ) ( ) e e x k i t i t u u y A A + = = 利用关系式 2π 2π T = = 和 uT = ,得
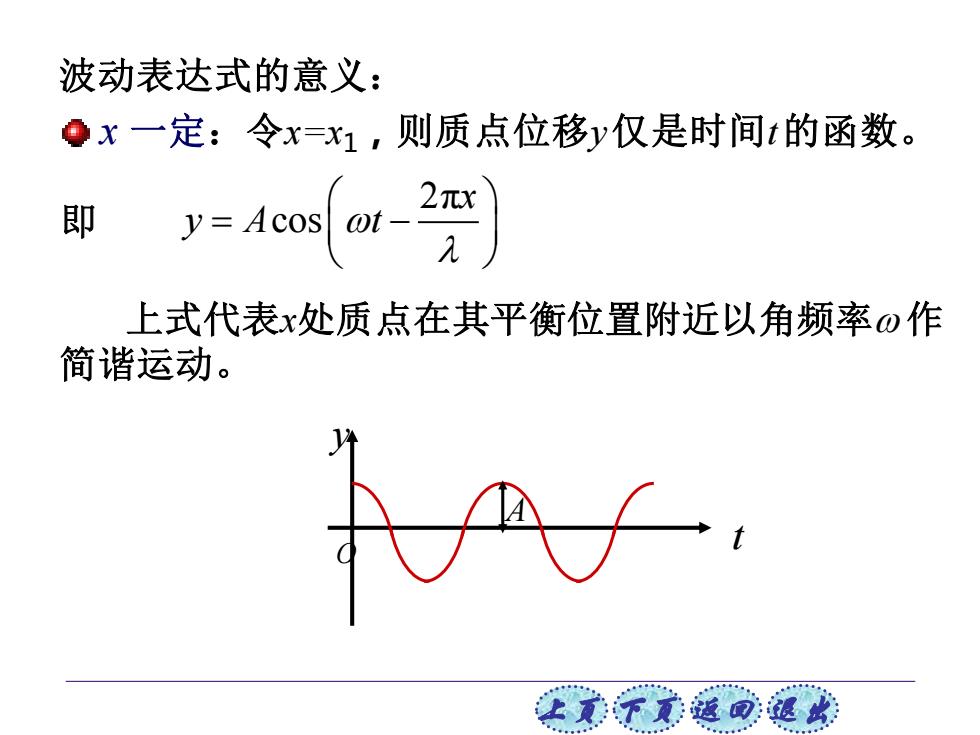
波动表达式的意义: Qx一定:令x=x1,则质点位移y仅是时间t的函数。 即 上式代表x处质点在其平衡位置附近以角频率o作 简谐运动。 让贰了意返可退此
上页 下页 返回 退出 波动表达式的意义: 上式代表x处质点在其平衡位置附近以角频率 作 简谐运动。 2π cos x y A t = − 即 x 一定:令x=x1,则质点位移y仅是时间t的函数。 t y O A
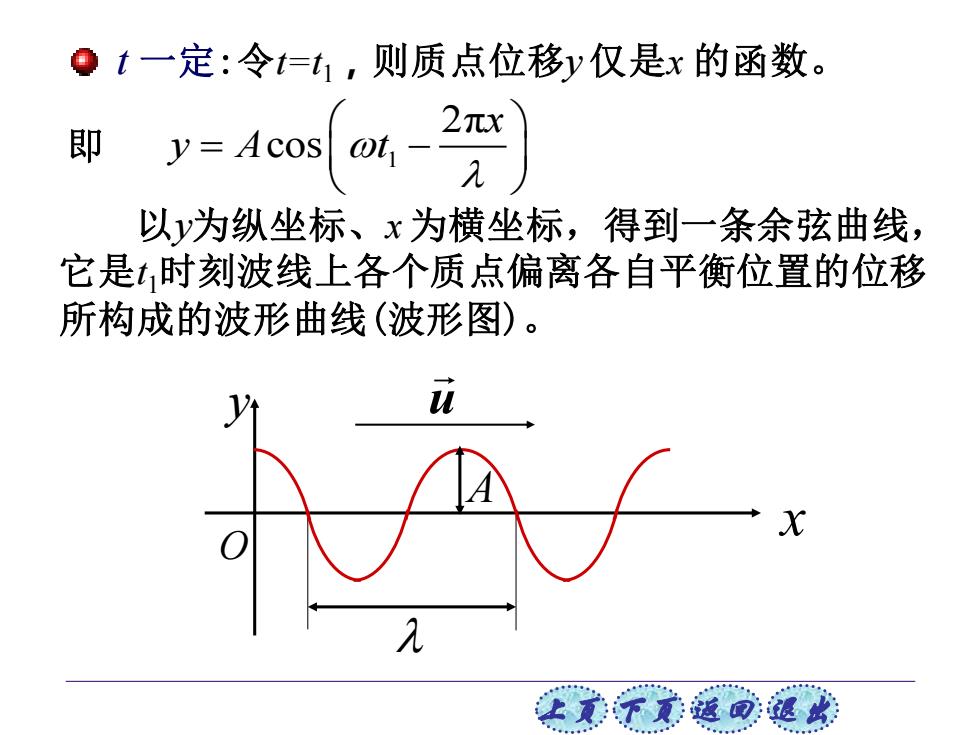
Qt一定:令t=t1,则质点位移y仅是x的函数。 2元x 即y=Acos( 以为纵坐标、x为横坐标,得到一条余弦曲线, 它是,时刻波线上各个质点偏离各自平衡位置的位移 所构成的波形曲线(波形图)。 让美下觉返同速
上页 下页 返回 退出 1 2π cos x y A t = − 即 以y为纵坐标、x 为横坐标,得到一条余弦曲线, 它是t1时刻波线上各个质点偏离各自平衡位置的位移 所构成的波形曲线(波形图)。 A u t 一定:令t=t1,则质点位移y 仅是x 的函数。 x y O
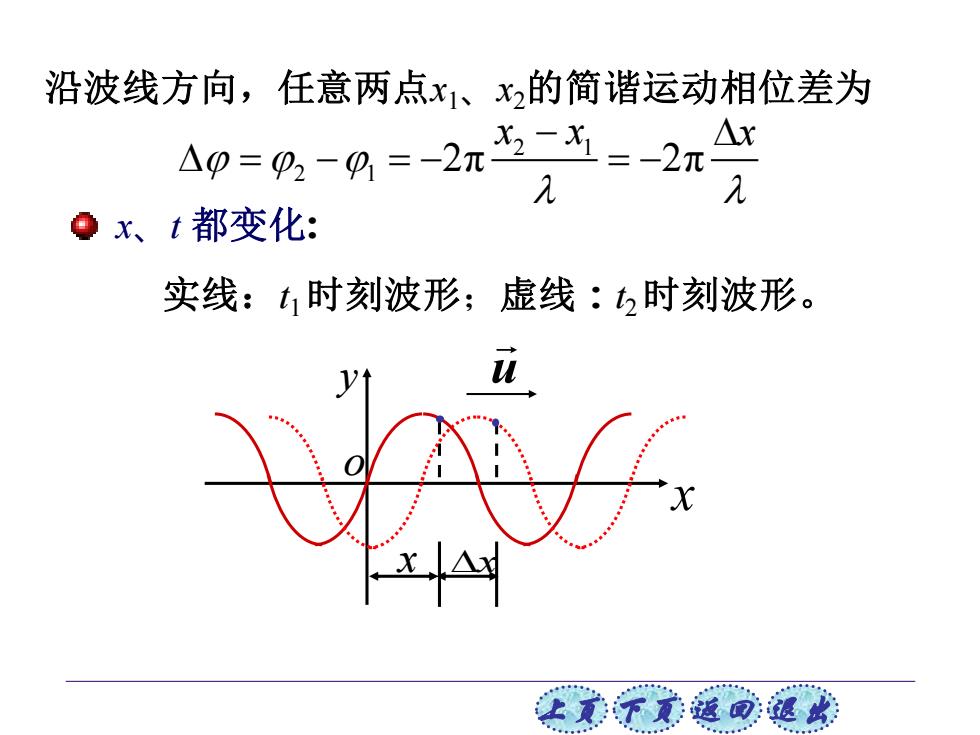
沿波线方向,任意两点x1、x2的简谐运动相位差为 △X △0=0,-0=-2元31=-2T2 ex、t都变化: 实线:t时刻波形;虚线:时刻波形。 正意子元道回退此
上页 下页 返回 退出 x 沿波线方向,任意两点x1、x2的简谐运动相位差为 2 1 2 1 2π 2π x x x − = − = − = − x、t 都变化: 实线:t1 时刻波形;虚线:t2 时刻波形。 u x x y o

当时y=o时o-负 当=4a时,y=4eoo+r-》+4] 在t和t+△时刻,对应的位移用x1和x,表示,则 a)=4cwo4-+我 %+0=ca4+w-}r] 让意文滋可退攻
上页 下页 返回 退出 当t=t 1时, + = 1 − 0 cos u x y A t 当t= t 1+Δt时, + = 1 + − 0 cos u x y A t t 在t 1和t 1+Δt时刻,对应的位移用x1和x2表示,则 1 1 1 0 ( ) cos x y t A t u = − + 2 1 1 0 ( ) cos x y t t A t t u + = + − +

令x2=x+△t,得 =y(t) 在△t时间内,整个波形向波的传播方向移动 了△x=x2一x1=u△t,波速u是整个波形向前传播 的速度。 让美不意返回退
上页 下页 返回 退出 1 1 1 0 ( ) cos x u t y t t A t t u + + = + − + 1 1 0 cos x A t u = − + 令 x x t 2 1 = + ,得 在Δt 时间内,整个波形向波的传播方向移动 了 ,波速u 是整个波形向前传播 的速度。 2 1 = − = x x x u t 1 = y t( )