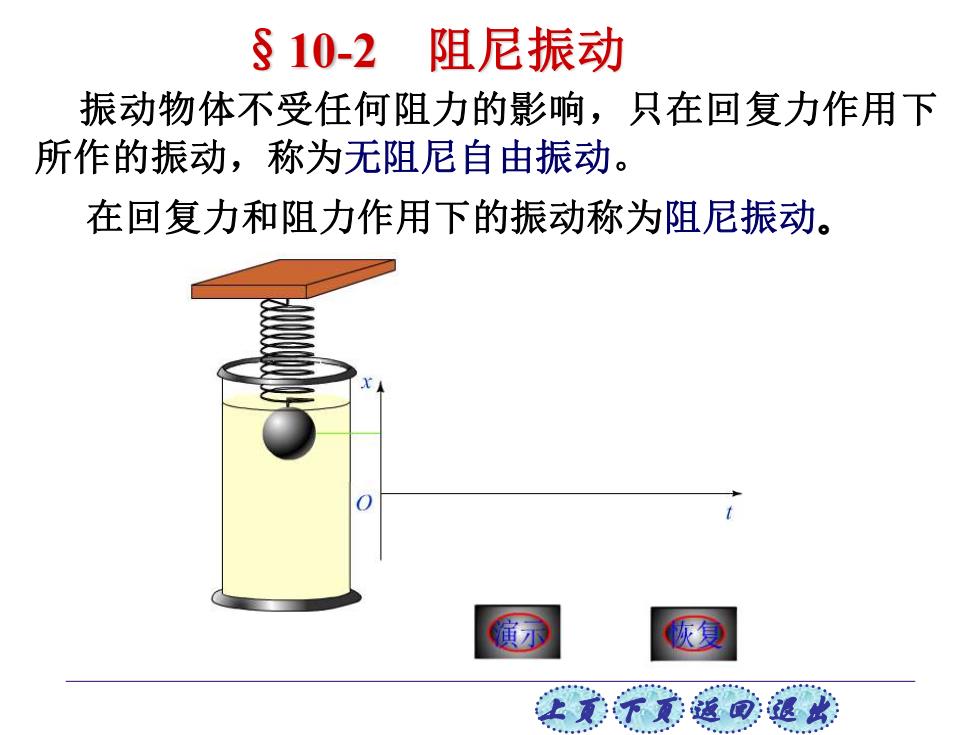
§10-2 阻尼振动 振动物体不受任何阻力的影响,只在回复力作用下 所作的振动,称为无阻尼自由振动。 在回复力和阻力作用下的振动称为阻尼振动。 恢夏 让贰子元道觉退此
上页 下页 返回 退出 振动物体不受任何阻力的影响,只在回复力作用下 所作的振动,称为无阻尼自由振动。 在回复力和阻力作用下的振动称为阻尼振动。 §10-2 阻尼振动

阻尼:消耗振动系统能量的原因。 阻尼种类:摩擦阻尼,辐射阻尼。 对在流体(液体、气体)中运动的物体,当物体速度 较小时,阻力大小正比于速度,且方向相反,表示为 dx F=-yv=-Ydi :阻力系数,其大小由物体的形状、大小和介质 的性质决定。 让美下觉返司速此
上页 下页 返回 退出 阻尼:消耗振动系统能量的原因。 阻尼种类:摩擦阻尼,辐射阻尼。 对在流体(液体、气体)中运动的物体,当物体速度 较小时,阻力大小正比于速度,且方向相反,表示为 f d d x F v t = − = − :阻力系数,其大小由物体的形状、大小和介质 的性质决定

在阻力作用下的弹簧振子 受力:弹性恢复力-阻力F d2x 运动方程:m =-kx-Ydi dx dr2 k 引入固有角频率“=o,阻尼系数 Y=26 m m dx+26dr +0x=0 dt 在小阻尼条件下(δ<⊙,),微分方程的解为 x=ecos(0't+4,),其中o'=√-6 上贰不觉返退此
上页 下页 返回 退出 在阻力作用下的弹簧振子 受力: 运动方程: 引入固有角频率 2 0 k m = 在小阻尼条件下 ( ) 0 ,微分方程的解为 ,其中 弹性恢复力 −kx 阻力 Ff 2 2 d d d d x x m kx t t = − − 2 2 2 0 d d 2 0 d d x x x t t + + = 0 0 e cos( ' ') t x A t − = + 2 2 0 ' = − 2 m ,阻尼系数 =
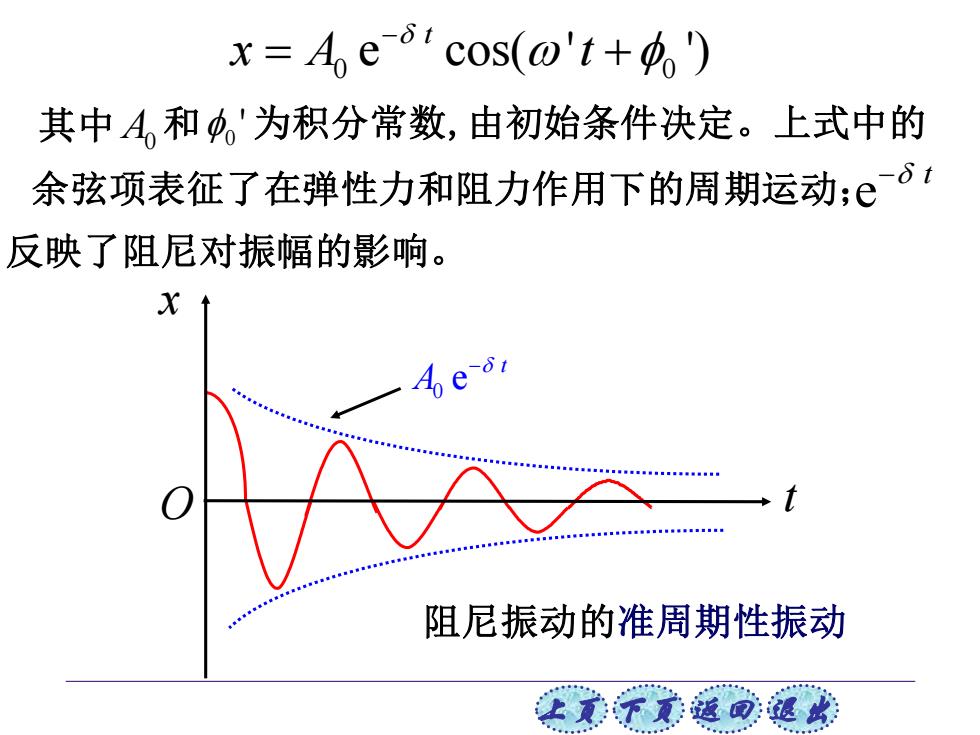
x=Aecos(@'+) 其中A,和,'为积分常数,由初始条件决定。上式中的 余弦项表征了在弹性力和阻力作用下的周期运动:ò1 反映了阻尼对振幅的影响。 X -ò1 阻尼振动的准周期性振动 让美下元返回:退欢
上页 下页 返回 退出 余弦项表征了在弹性力和阻力作用下的周期运动; 反映了阻尼对振幅的影响。 e − t 0 e t A − t x O 0 0 e cos( ' ') t x A t − = + A0 ' 其中 和 0 为积分常数,由初始条件决定。上式中的 阻尼振动的准周期性振动

阻尼振动不是周期性振动,更不是简谐振动,因位移 不是时间的周期函数。但阻尼振动有某种重复性。 位移相继两次达到极大值的时间间隔叫做阻尼振 动的周期,有 2π 2元 T'= 2 oj-8 00 显而易见,由于阻尼,振动变慢了。 阻尼振动的振幅为 A=Aoe- 振幅随时间作指数衰减。阻尼δ大小决定了 阻尼振动振幅的衰减程度
上页 下页 返回 退出 阻尼振动不是周期性振动,更不是简谐振动,因位移 不是时间的周期函数。但阻尼振动有某种重复性。 位移相继两次达到极大值的时间间隔叫做阻尼振 动的周期,有 显而易见,由于阻尼,振动变慢了。 阻尼振动的振幅为 阻尼振动振幅的衰减程度。 2 2 0 0 2π 2π 2π ' ' T = = − 0 e t A A − = 振幅随时间作指数衰减。阻尼 大小决定了
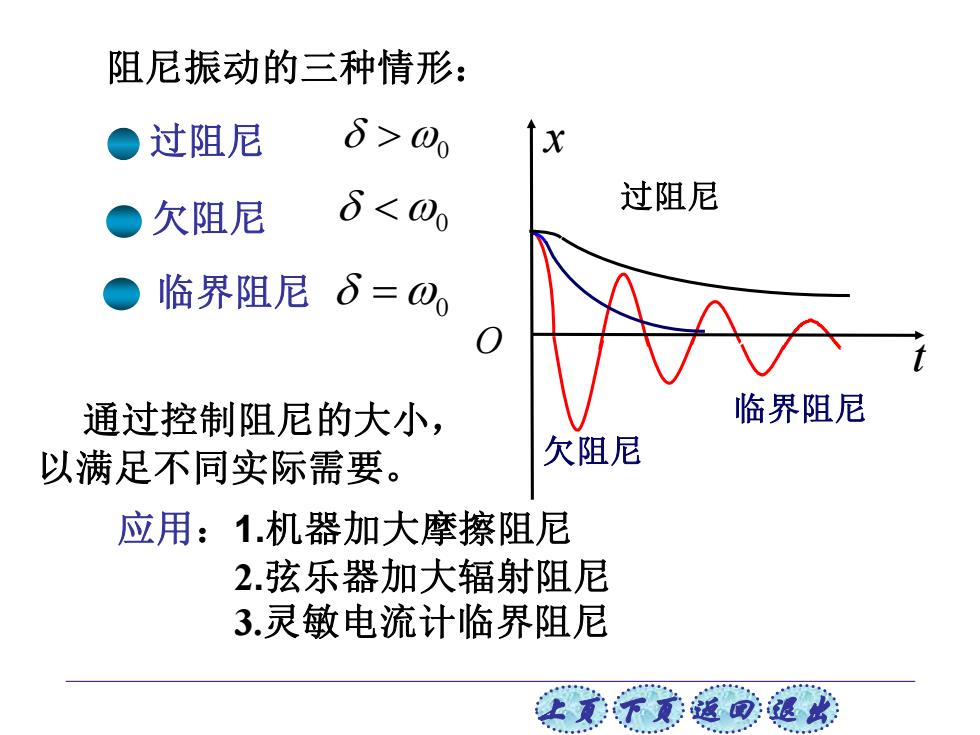
阻尼振动的三种情形: ●过阻尼 6>00 。欠阻尼 6<0 过阻尼 ● 临界阻尼δ=0, 通过控制阻尼的大小, 临界阻尼 以满足不同实际需要。 欠阻尼 应用:1.机器加大摩擦阻尼 2.弦乐器加大辐射阻尼 3.灵敏电流计临界阻尼 让美下觉返同速
上页 下页 返回 退出 阻尼振动的三种情形: 临界阻尼 过阻尼 欠阻尼 欠阻尼 过阻尼 临界阻尼 通过控制阻尼的大小, 以满足不同实际需要。 0 0 0 = x O t 应用:1.机器加大摩擦阻尼 3.灵敏电流计临界阻尼 2.弦乐器加大辐射阻尼

选择进入下一节 §10-0 教学基本要求 §10-1 谐振动 §10-2 阻尼振动 §10-3 受迫振动 共振 §10-4 电磁振荡 §10-5 一维谐振动的合成 *§10-6 二维谐振动的合成 *§10-7 振动的分解频谱 *§10-8 非线性振动与混沌 正意子元道回退此
上页 下页 返回 退出 选择进入下一节 §10-0 教学基本要求 §10-1 谐振动 §10-2 阻尼振动 §10-3 受迫振动 共振 §10-4 电磁振荡 §10-5 一维谐振动的合成 *§10-6 二维谐振动的合成 *§10-7 振动的分解 频谱 *§10-8 非线性振动与混沌