
§10-5 一维谐振动的合成 一、同一直线上两个同频率的谐振动的合成 设一质点同时参与沿同一方向(x轴)的两个独 立的同频率的简谐振动,两个振动位移为 x=A cos(ot+o)x2=4 cos(ot+o) 合位移:x=x,+x2=Ac0s(Ot+4) 其中A=√A+AG+2A4c0s(0-4o) tan或=4sin4。+4sin4 A1c0S中0+A2c0Sp0 合振动仍然是简谐振动,其方向和频率与原来相同。 上意不元返回退此
上页 下页 返回 退出 设一质点同时参与沿同一方向(x轴)的两个独 立的同频率的简谐振动,两个振动位移为 合位移: 2 2 1 2 1 2 20 10 A A A A A = + + − 2 cos( ) 合振动仍然是简谐振动,其方向和频率与原来相同。 1 10 2 20 0 1 10 2 20 sin sin tan cos cos A A A A + = + 一、同一直线上两个同频率的谐振动的合成 1 1 10 x A t = + cos( ) 2 2 20 x A t = + cos( ) 1 2 0 x x x A t = + = + cos( ) 其中 §10-5 一维谐振动的合成

旋转矢量图示法 4=4+4 X A矢量沿x轴之投影表征了合运动的规律。 A=√A+A+2 44 cos(0-40) 江美不意返向退此
上页 下页 返回 退出 旋转矢量图示法 O x 10 20 1 x 2 x x 2 2 1 2 1 2 20 10 A A A A A = + + − 2 cos( ) A 矢量沿x轴之投影表征了合运动的规律。 A1 A2 A A A = +1 2
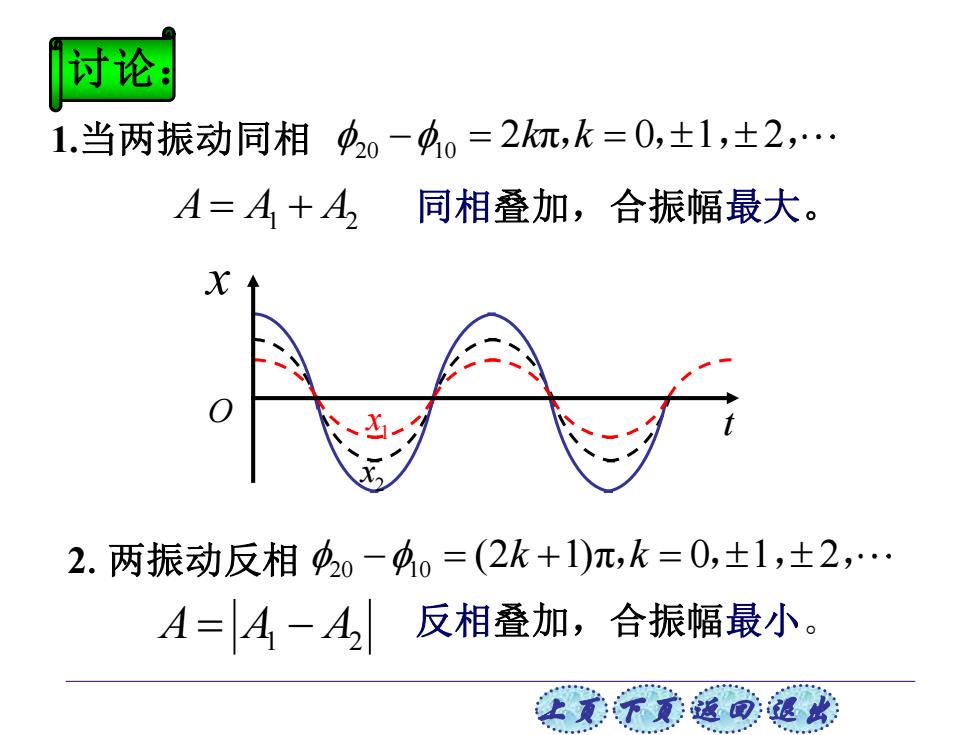
讨论 1.当两振动同相0-40=2km,k=0,±1,士2,. A=A+A,同相叠加,合振幅最大。 2.两振动反相420-40=(2k+1)π,k=0,±1,士2,. A=4-4 反相叠加,合振幅最小
上页 下页 返回 退出 1.当两振动同相 A = A1 + A2 同相叠加,合振幅最大。 20 10 − = = 2k k π, 0 1 2 , , , t x 1 x 2 x 讨论: 2.两振动反相 A = A1 − A2 反相叠加,合振幅最小。 20 10 − = + = (2 1) k k π, 0 1 2 , , , O
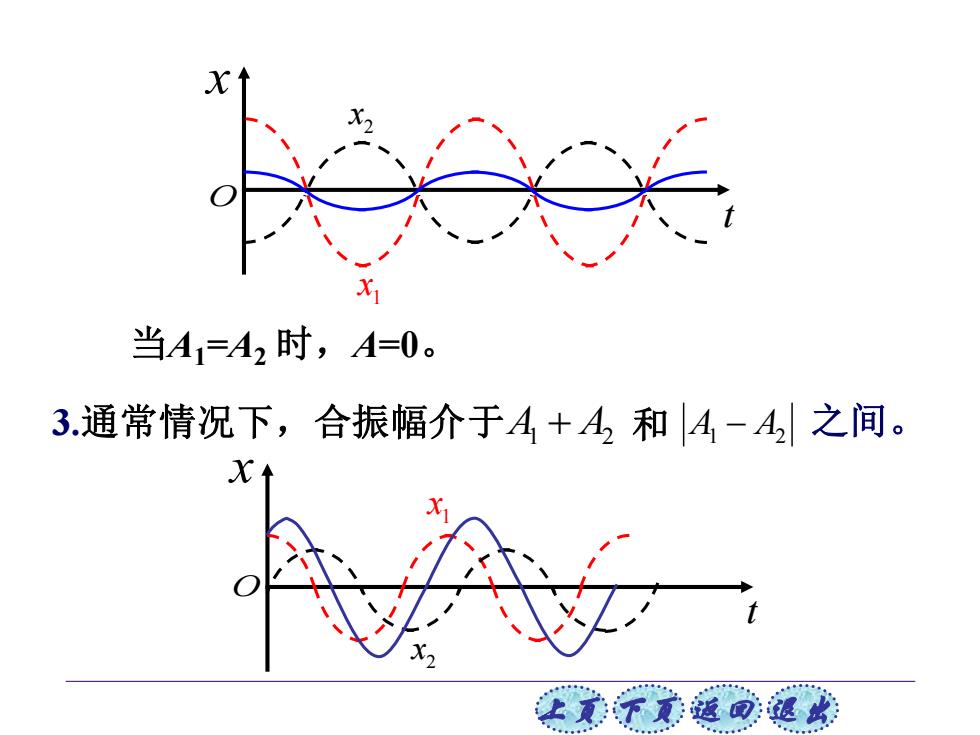
当A1=A2时,A=0。 3.通常情况下,合振幅介于A+A,和A-A之间。 王觉下元菠面:退收
上页 下页 返回 退出 当A1=A2 时,A=0。 t x 1 x 2 x 3.通常情况下,合振幅介于 A1 + A2 和 A1 − A2 之间。 t x 1 x 2 x O O

例题10-6N个同方向、同频率的简谐振动,它们的振 幅相等,初相分别为0424.34,.,依次差一个恒量4。, 振动表达式可写成: x=acosot x2 acos(@t+) x3=ac0s(ot+24)) xN acos[ot+(N-1)] 求它们的合振动的振幅和初相。 解:采用旋转矢量法可使问题得到简化,从而避开繁 琐的三角函数运算。 根据矢量合成法则,N个简谐振动对应的旋转矢量的 合成如下图所示:
上页 下页 返回 退出 例题10-6 N个同方向、同频率的简谐振动,它们的振 求它们的合振动的振幅和初相。 解:采用旋转矢量法可使问题得到简化,从而避开繁 琐的三角函数运算。 根据矢量合成法则,N个简谐振动对应的旋转矢量的 合成如下图所示: x acost 1 = 2 0 x a t = + cos( ) 3 0 x a t = + cos( 2 ) 0 cos[ ( 1) ] N x a t N = + − 振动表达式可写成: 幅相等,初相分别为 0 0 0 0 2 3 , , , , , 依次差一个恒量 0

X a P 因各个振动的振幅相同且相差依次恒为4,上图 中各个矢量的起点和终点都在以C为圆心的圆周上, 令其半径为R,根据简单的几何关系,可得 ∠OCM=N4 让美觉返司退
上页 下页 返回 退出 O x 1 a 2 a 3 a 4 a a5 0 0 0 0 C A M 根据简单的几何关系,可得 中各个矢量的起点和终点都在以 C为圆心的圆周上, 因各个振动的振幅相同且相差依次恒为 0 ,上图 = OCM N0 令其半径为R, 0 P

在三角形OCM中,OM的长度就是合振动位移矢量 的位移,角度∠MOP就是合振动的初相,据此得 A=2Rsin Nφo 2 考虑到 a 2Rsin 4 2 sin N A-a 2 2 让美子美通回退此
上页 下页 返回 退出 考虑到 在三角形OCM中,OM 的长度就是合振动位移矢量 的位移,角度 MOP 就是合振动的初相,据此得 0 2 sin 2 N A R = 0 2 sin 2 a R = 0 0 sin 2 sin 2 N A a =

合振动初位相 =∠MOP=∠COP-∠COM 红-)方-) 可得合振动的表达式 N sin W-1 x=Acos(ot+)=a 2 cos(@t+- 2 当,=0时(同相合成),有A=Na 6=0 合振幅最大 让美觉返司退
上页 下页 返回 退出 0 = = − MOP COP COM 0 0 0 1 1 1 (π ) (π ) 2 2 2 N N − = − − − = 合振动初位相 可得合振动的表达式 0 0 0 0 sin 2 1 cos( ) cos( ) 2 sin 2 N N x A t a t − = + = + 当 0 = 0 时(同相合成),有 A Na = 0 = 0 合振幅最大

二、同一直线上两个不同频率的谐振动的合成拍 当两个同方向简谐振动的频率不同时,在旋转矢 量图示法中两个旋转矢量的转动角速度不相同,二者 的相位差与时间有关,合矢量的长度和角速度都将随 时间变化。 两个简谐振动的频率0和02很接近,且02>01 x1=AC0s(Ot+4),x2=A2C0(o2t+4) 两个简谐振动合成得 x=x+x2 x=2Ac0s(%,90-c0s(@+m1+4) 2 2
上页 下页 返回 退出 两个简谐振动合成得 当两个同方向简谐振动的频率不同时,在旋转矢 量图示法中两个旋转矢量的转动角速度不相同,二者 的相位差与时间有关,合矢量的长度和角速度都将随 时间变化。 x = x1+ x2 1 1 0 0 cos( ), cos( ) 1 2 2 2 x A t x A t = + = + 二、同一直线上两个不同频率的谐振动的合成 拍 两个简谐振动的频率 1 和 2 很接近,且 2 1 2 1 2 1 0 2 cos( ) cos( ) 2 2 x A t t − + = +

因01~02,02-01<<0或02,有 02+01≈0,≈01 2 在两个简谐振动的位移合成表达式中,第一项随时 间作缓慢变化,第二项是角频率近于01或0,的简谐函 数。合振动可视为是角频率为(@,+⊙2)/2、振幅为 2Acos(@2-0)t/2的简谐振动。 合振动的振幅随时间作缓慢的周期性的变化,振 动出现时强时弱的拍现象。 拍频:单位时间内强弱变化的次数。 02-01 =2-l 2π 让美觉返司退
上页 下页 返回 退出 合振动的振幅随时间作缓慢的周期性的变化,振 动出现时强时弱的拍现象。 拍频:单位时间内强弱变化的次数。 因 1 2 ~ , 2 1 1 − 或 2 , 有 2 1 1 2 2 + 在两个简谐振动的位移合成表达式中,第一项随时 间作缓慢变化, 第二项是角频率近于 的简谐函 数。合振动可视为是角频率为 、振幅为 的简谐振动。 1 2 ( ) 2 + 2 1 2 cos( ) 2 A t − 1 或 2 2 1 2 1 1 2π − = = = −