
§11-6电磁波 变化的电场和变化的磁场不断地交替产生,由近及远 以有限的速度在空间传播,形成电磁波。最初由麦克斯 韦在理论上预言,1887年赫兹进行了实验证实。 让美子元返司退
上页 下页 返回 退出 变化的电场和变化的磁场不断地交替产生,由近及远 以有限的速度在空间传播,形成电磁波。最初由麦克斯 韦在理论上预言,1887年赫兹进行了实验证实。 §11-6 电磁波
一、 电磁波的辐射和传播 振荡偶极子:电流在直线形电路中往复振荡,两 端出现正负交替的等量异号电荷。 用 e 任何振动电荷或电荷系都是发射电磁波的波源, 如天线中振荡的电流、原子或分子中电荷的振动都会 在其周围空间产生电磁波。 提高振荡电流辐射电磁场的方法 00 上美不贰返可退
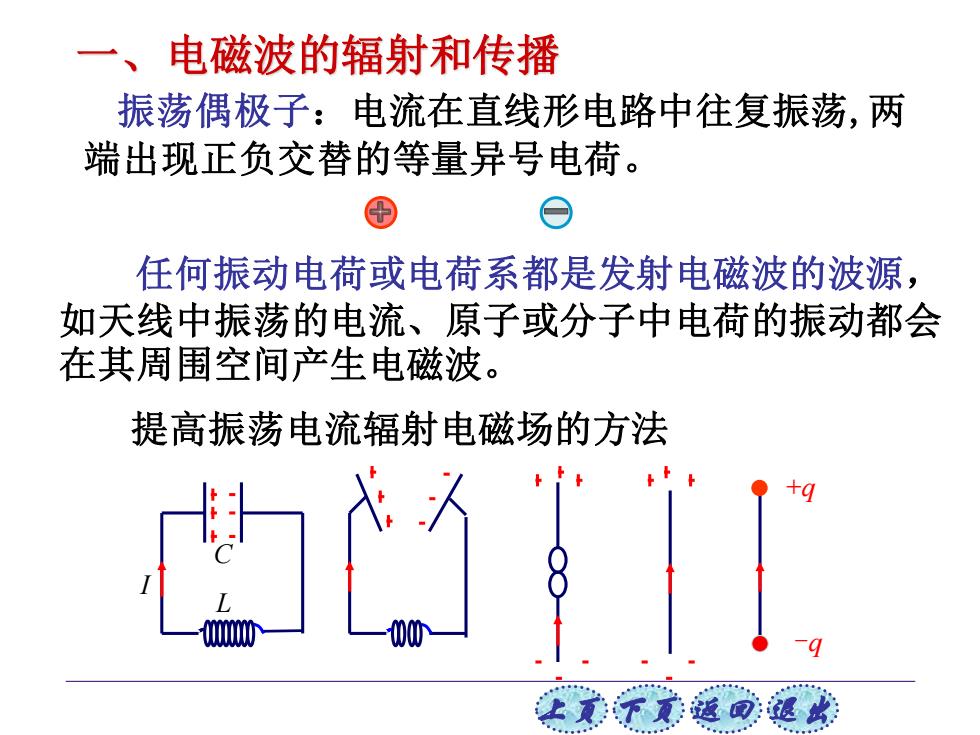
上页 下页 返回 退出 提高振荡电流辐射电磁场的方法 任何振动电荷或电荷系都是发射电磁波的波源, 如天线中振荡的电流、原子或分子中电荷的振动都会 在其周围空间产生电磁波。 I L C +q -q 振荡偶极子:电流在直线形电路中往复振荡,两 端出现正负交替的等量异号电荷。 一、电磁波的辐射和传播
1887年,赫兹实验 赫兹实验 B 让美觉返司退
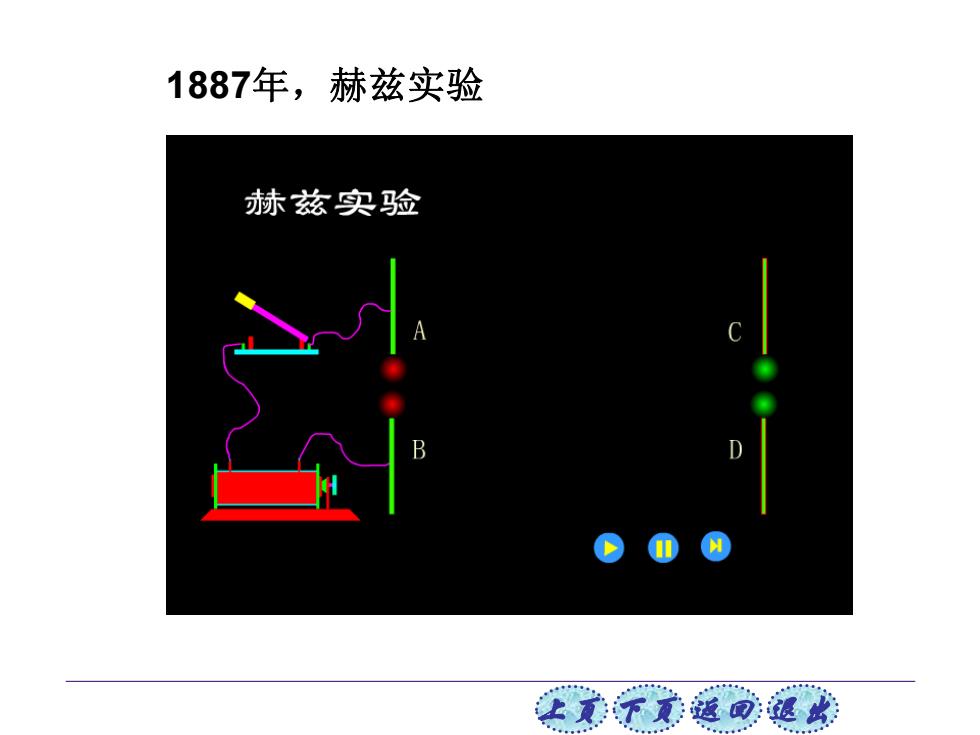
上页 下页 返回 退出 1887年,赫兹实验
振荡偶极子电矩:p。=po cos wt 一条闭合电场线的形成过程 振荡电偶极子不仅产生电 场,而且产生磁场。振荡电 偶极子周围的电磁场线如右 图所示: 意子元道回退瑞
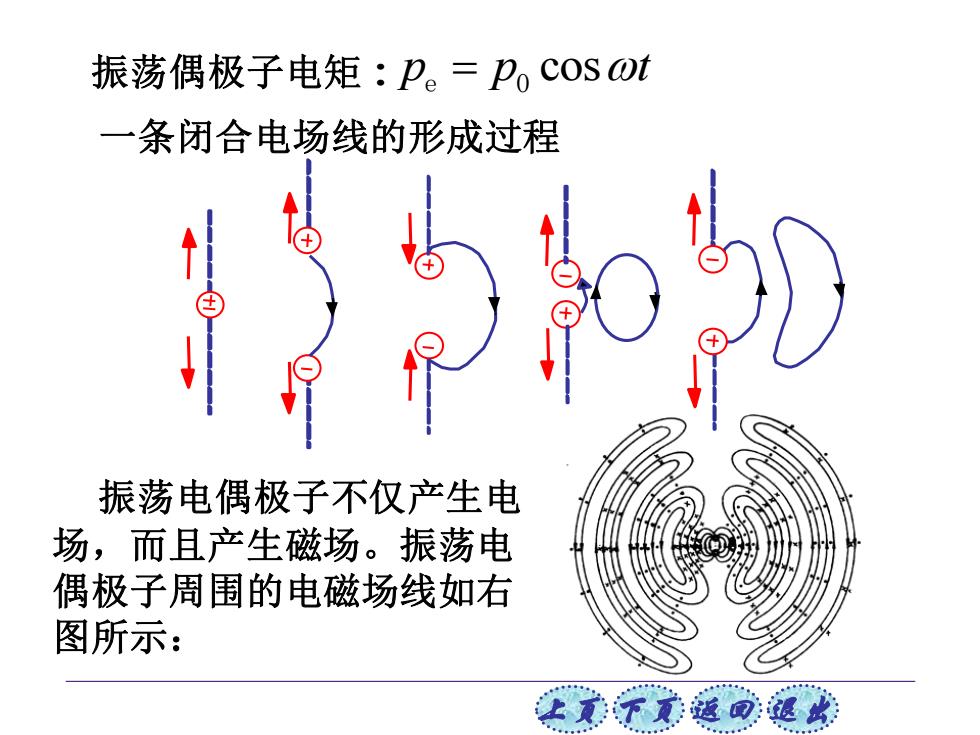
上页 下页 返回 退出 振荡偶极子电矩: 0 cos e p p t = 一条闭合电场线的形成过程 振荡电偶极子不仅产生电 场,而且产生磁场。振荡电 偶极子周围的电磁场线如右 图所示:

振荡偶极子在真空中、远离偶极子的P点处、在时刻 的E、H的量值可表为 B=E。= @posine 4r6c27 cos@ H=, posine 让美下觉返同速
上页 下页 返回 退出 振荡偶极子在真空中、远离偶极子的P点处、在时刻 t 的E、H 的量值可表为 2 0 2 0 sin cos 4 p r E E t c r c = = − π 2 0 sin cos 4 p r H H t cr c = = − π

即 E=6w-ka2行月 H=,eosn)Eos2r[是 分别对x及求二阶偏导: OE 18E 8r su &x2 a2H1∂2H /u 812 su ax2 上意不意道可退欢
上页 下页 返回 退出 0 0 cos cos 2 x t x E E t E c T = − = − π 即 0 0 cos cos 2 x t x H H t E c T = − = − π 分别对x及t求二阶偏导: 2 2 2 2 E E 1 t x = 2 2 2 2 H H 1 t x = 1 u =
平面简谐电磁波的传播 二、电磁波的性质 1.横波 2.偏振性 3.E和H同相位 4.E和H量值成比例 EE=√uH 1 5.电磁波的传播速度为u= 通常和山与电磁波的频率有关,在介质中不同频 率的电磁波具有不同的传播速度,此即电磁波在介质 中的色散现象。 让美下觉返司速此
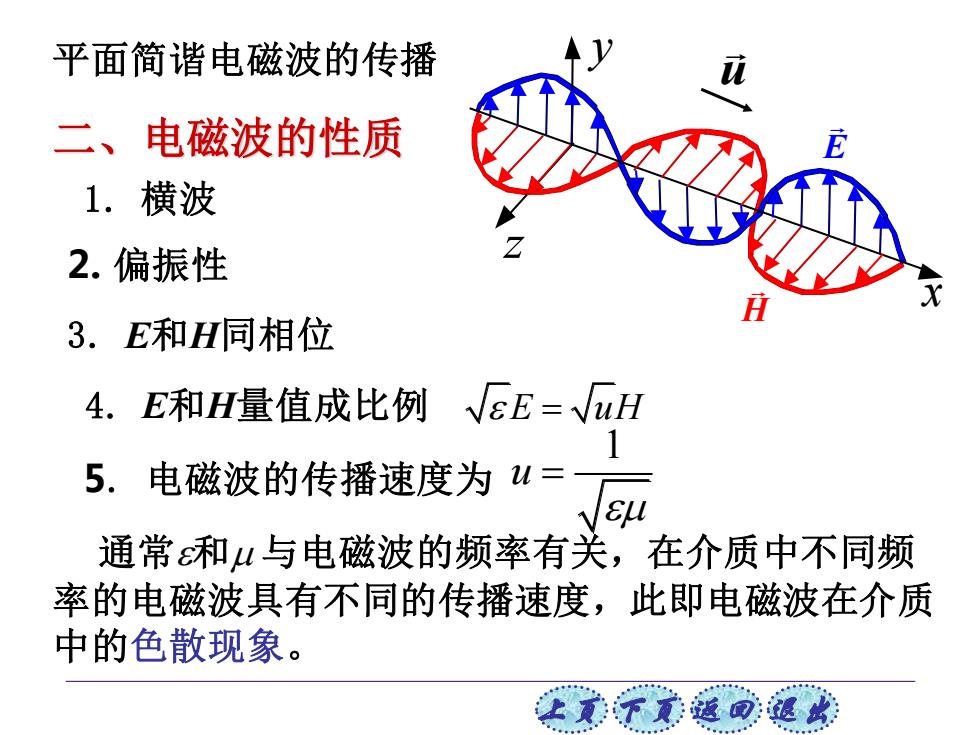
上页 下页 返回 退出 二、电磁波的性质 1. 横波 4. E和H量值成比例 2. 偏振性 3. E和H同相位 5. 电磁波的传播速度为 通常和 与电磁波的频率有关,在介质中不同频 率的电磁波具有不同的传播速度,此即电磁波在介质 中的色散现象。 E uH = 1 u = u E H x y z 平面简谐电磁波的传播

三、电磁波的能量 电磁波所携带的电磁能量,称为辐射能。单位时间内 通过垂直于传播方向的单位面积的辐射能,称为能流密 度或辐射强度。 电场和磁场的能量体密度分别为 8E2 W= MH2 2, 2 电磁场的总能量体密度: w=形。+地= εE2+WH2 2 辐射能量的传播速度是电磁波的传播速度,辐射能的 传播方向是电磁波的传播方向
上页 下页 返回 退出 电磁波所携带的电磁能量,称为辐射能。单位时间内 通过垂直于传播方向的单位面积的辐射能,称为能流密 度或辐射强度。 电场和磁场的能量体密度分别为 2 2 , 2 2 E H w w e m = = 电磁场的总能量体密度: 2 2 2 E H w w w + = + = e m 辐射能量的传播速度是电磁波的传播速度,辐射能的 传播方向是电磁波的传播方向。 三、电磁波的能量

能流密度矢量S S=ww=(eE+HH)=EH E H S=Ex豆 辐射强度矢量S也称为坡印廷(J.H.Poynting)矢量。 让美觉返司退
上页 下页 返回 退出 ( ) 2 2 2 u S wu E H EH = = + = 能流密度矢量 S S E H = S H E 辐射强度矢量S 也称为坡印廷(J. H. Poynting)矢量

考虑平面余弦电磁波的情形 s o 取一个周期内的平均值,cos2[o(t-x/u)+时间 平均值为1/2,平均辐射强度 =E,H。 21 因c=1/V84以及V8E=√4H,得 s=ue 让美不意返回退此
上页 下页 返回 退出 考虑平面余弦电磁波的情形 2 0 0 0 cos x S E H t u = − + 取一个周期内的平均值, 的时间 平均值为1/2,平均辐射强度 ( ) 0 2 cos t − x / u + 0 0 1 2 S E H = 因 c =1 00 以及 0E0 = 0H0 ,得 2 0 0 1 2 S cE = 2 0 0 1 2 S cH =