§9-5磁场的能量 在回路系统中通以电流时,由于各回路的自感 和相互之间的互感的作用,回路中的电流要经历一 个从零到稳定值的过程,在这个过程中,电源必须 提供能量来克服自感电动势及互感电动势而作功, 使电能转化为载流回路的能量和回路电流之间的相 互作用能,也就是磁场能。 D 下面以图示 电路为例进 行讨论 让美觉返司退
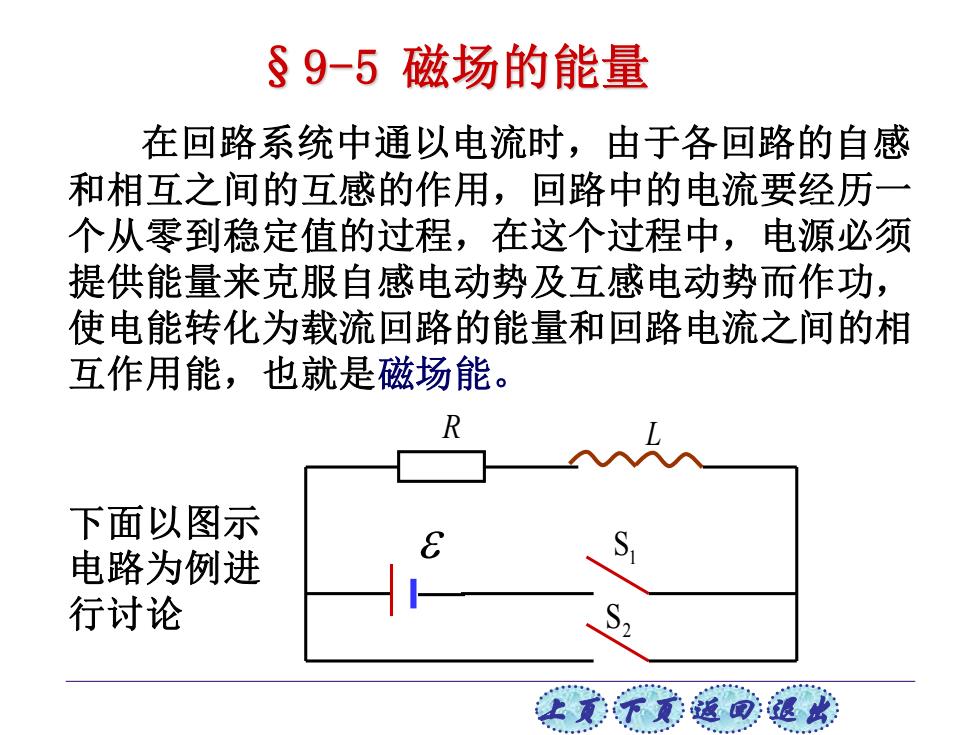
上页 下页 返回 退出 §9-5 磁场的能量 在回路系统中通以电流时,由于各回路的自感 和相互之间的互感的作用,回路中的电流要经历一 个从零到稳定值的过程,在这个过程中,电源必须 提供能量来克服自感电动势及互感电动势而作功, 使电能转化为载流回路的能量和回路电流之间的相 互作用能,也就是磁场能。 下面以图示 电路为例进 行讨论 S1 R L S2
设电路接通后回路中某瞬时的电流为,自感电动 势为-d!,由欧姆定律得 d 8-L IR dt Cddt=Ldl+fRrdr 正贰子元道同退此
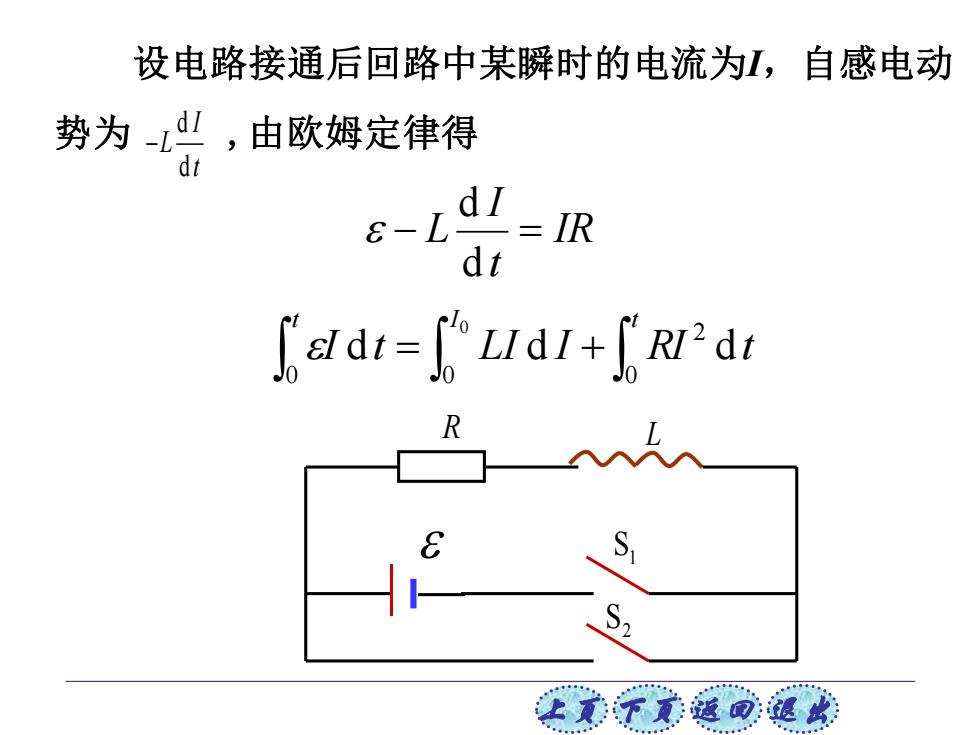
上页 下页 返回 退出 设电路接通后回路中某瞬时的电流为I,自感电动 势为 d ,由欧姆定律得 d I L t − IR t I − L = d d = + t I t I t LI I RI t 0 2 0 0 d d d 0 S1 R L S2

在自感和电流无关的情况下 odi-t+Rd ∫rdt是t时间内电源提供的部分能量转化为消 耗在电阻P上的焦耳-楞次热。 是回路中建立电流的暂态过程中电源电动 势克服自感电动势所作的功,这部分功转化为载流 回路的能量;这部分能量也是储存在磁场中的能量。 当回路中的电流达到稳定值后,断开$,并同 时接通S2,这时回路中的电流按指数规律衰减,此 电流通过电阻时,放出的焦耳-楞次热为 让美觉返司退
上页 下页 返回 退出 在自感和电流无关的情况下 = + t t I t LI RI t 0 2 2 0 d 2 1 d 0 是 时间内电源提供的部分能量转化为消 耗在电阻 上的焦耳-楞次热。 t RI t 0 2 d R 是回路中建立电流的暂态过程中电源电动 势克服自感电动势所作的功,这部分功转化为载流 回路的能量;这部分能量也是储存在磁场中的能量。 2 0 1 2 LI 当回路中的电流达到稳定值后,断开 ,并同 时接通 ,这时回路中的电流按指数规律衰减,此 电流通过电阻时,放出的焦耳-楞次热为 S1 S2 t

Q=[RI'dt =RIe dt 2 这说明随着电流衰减引起的磁场消失,原来储存 在磁场中的能量又反馈到回路中以热能的形式全 部释放出来,也说明磁场具有能量。L1的推断是 正确的。因此磁场能量可表示为 磁
上页 下页 返回 退出 = 0 2 Q RI dt − = 0 2 2 RI 0 e dt t L R 2 0 2 1 = LI 2 m 0 2 1 W = LI 磁 能 这说明随着电流衰减引起的磁场消失,原来储存 在磁场中的能量又反馈到回路中以热能的形式全 部释放出来,也说明磁场具有能量 的推断是 正确的。因此磁场能量可表示为 2 0 1 2 LI

对于一个很长的内部充满磁导率为的直螺线管,有 B=umnI,L=u2V 则 Wm= v=BHV 1B2 2 u 2 磁能 密度 1 2=BH 2 u 2 上式是从直螺线管的均匀磁场的特例导出的,对于 般情况的均匀磁场,磁场能量密度可以表示为 W B.H 2 让美觉返司退此
上页 下页 返回 退出 磁能 密度 H BH B V W w 2 1 2 1 2 1 2 2 m m = = = = B nI L n V 2 = , = V BHV B W 2 1 2 1 2 m = = 对于一个很长的内部充满磁导率为µ的直螺线管,有 上式是从直螺线管的均匀磁场的特例导出的,对于 一般情况的均匀磁场,磁场能量密度可以表示为 w B H = 2 1 m 则

对于非均匀磁场 dwm =wm dv= BH dV 总磁 能 .d 故 -r 可见,如能按照上式右面积分先求出电流回路的磁 场能量,根据上式也可求出回路的自感。这是计算 自感的一种重要方法。(见例题9-11) 让美不意返回退此
上页 下页 返回 退出 W w V BH dV 2 1 d d m = m = W = BH dV 2 1 m LI = BH dV 2 1 2 1 2 总磁 能 对于非均匀磁场 2 m 0 2 1 又 W = LI 可见,如能按照上式右面积分先求出电流回路的磁 场能量,根据上式也可求出回路的自感。这是计算 自感的一种重要方法。(见例题9-11) 故

电场能量与磁场能量的比较 电场能量 磁场能量 电容器储能 自感线圈储能 cr-or- 20 电场能量密度 磁场能量密度 1 1 B2 地ED2汤5 Wm= 24o4: 电场能量W。=wd业 磁场能量, 能量法求C 能量法求L 王觉不元菠面:退收
上页 下页 返回 退出 电场能量与磁场能量的比较 电场能量 磁场能量 电容器储能 自感线圈储能 电场能量密度 磁场能量密度 磁场能量 能量法求L 电场能量 能量法求C C Q CV QV 2 2 1 2 1 2 2 = = 2 2 1 LI 0 r 2 m 2 2 1 B w = BH = 2 e 0 r 2 1 2 1 w = ED = E W w V V e e d = W w V V m m d =

例题9-11一根很长的同轴电缆由半径为R的圆柱体和 半径为R2的同心圆柱壳组成,电缆中央的导体上载有 稳定电流I,再经外层导体返回形成闭合回路。试计算 (1)长为的一段电缆内的磁场中所储藏的能量(2) 该段电缆的自感。 让贰下觉返回退此
上页 下页 返回 退出 例题9-11 一根很长的同轴电缆由半径为R1的圆柱体和 半径为R2的同心圆柱壳组成,电缆中央的导体上载有 稳定电流I,再经外层导体返回形成闭合回路。试计算 (1)长为l 的一段电缆内的磁场中所储藏的能量(2) 该段电缆的自感。 I dr I r R1 R2 l R1 dr r R1

解:(1)由安培环路定理可知,在内外导体间的 区域内距轴线为处的磁感应强度为 B= l 2πr 电缆外磁感应强度为零,所以,磁能储藏在两个 导体之间的空间内。距轴线为r处的磁能密度为 1B2_412 Wm= 20 8元2r2 距轴线为到+dr处的磁能为 dwn =WdV=to!2 8r,2wdl=4/1d山r 4π 让美下元返回退欢
上页 下页 返回 退出 解:(1)由安培环路定理可知,在内外导体间的 区域内距轴线为r处的磁感应强度为 r I B 2π = 电缆外磁感应强度为零,所以,磁能储藏在两个 导体之间的空间内。距轴线为r处的磁能密度为 2 2 2 0 0 2 m 2 8π 1 r B I w = = 距轴线为r到 r+dr处的磁能为 r rl r I W w V 2π d 8π d d 2 2 2 0 m m = = r I l dr 4π 2 0 =

对上式积分可得储藏在内外导体之间的磁能为 戌=wd亚=4,/d业-n飞 4元 JR 4π R (2) 因 与(1)所求结果比较即可得 L= 2w=Lol in Ra 2元R 上面所得结果是假定高频电流在芯线表面流过,圆 柱状的芯线作为圆简处理,简内磁场为零。对于恒 定电流,电流分布在整个芯线导体截面内,导体截 面内磁场不为零。这种情况下求解如下: 上美子贰返回:退
上页 下页 返回 退出 对上式积分可得储藏在内外导体之间的磁能为 = = 2 1 d 4π d 2 0 m m R V R r I l r W w V 1 2 2 0 ln 4π R I l R = (2) 2 m 2 1 W = LI 与(1)所求结果比较即可得 1 0 2 2 m ln 2π 2 R l R I W L = = 上面所得结果是假定高频电流在芯线表面流过,圆 柱状的芯线作为圆筒处理,筒内磁场为零。对于恒 定电流,电流分布在整个芯线导体截面内,导体截 面内磁场不为零。这种情况下求解如下: 因