§8-31 毕奥一萨伐尔定律 一、毕奥一萨伐尔(Biot-Savart)定律 载流导线中的电流为I, 导线半径比到观察点P的距离 小得多,即为线电流。在线 电流上取长为d的定向线元, 规肩1的方向与电流的方向 相同1d7为电流元。 让美下觉返司速此
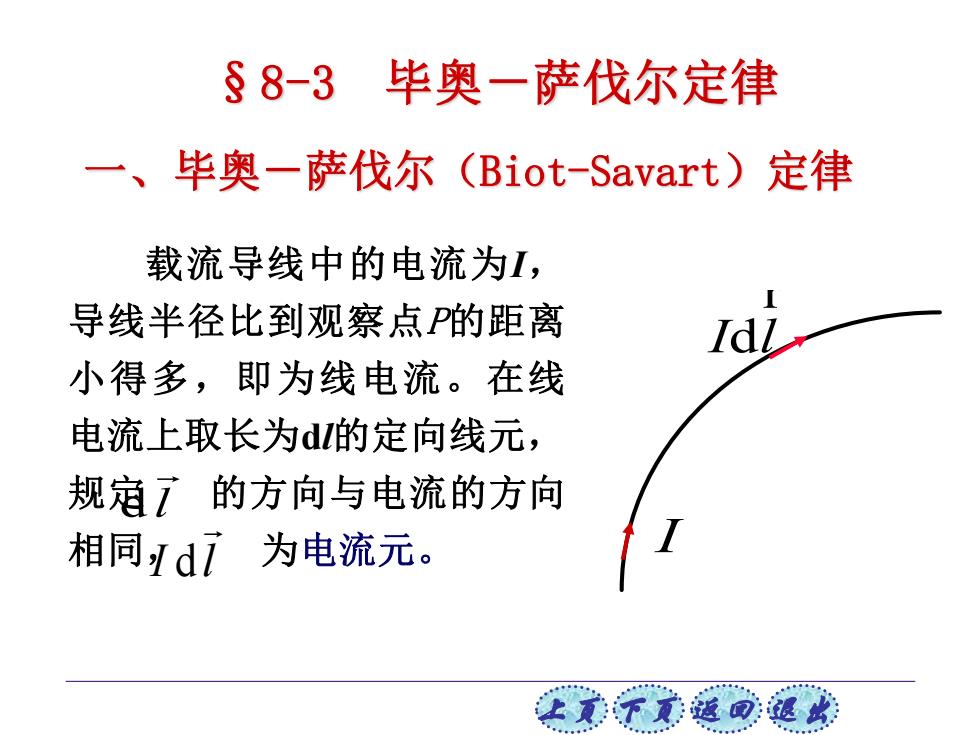
上页 下页 返回 退出 §8-3 毕奥-萨伐尔定律 一、毕奥-萨伐尔(Biot-Savart)定律 载流导线中的电流为I, 导线半径比到观察点P的距离 小得多,即为线电流。在线 电流上取长为dl的定向线元, 规定 的方向与电流的方向 相同, I l 为电流元。 d l d I I l d r
I dB d B d 电流元在给定点所产生的磁感应强度的大小与 l成正比,与到电流元的距离平方成反比,与电 流元和矢径夹角的正弦成正比。dB方向垂直于下 与Idl组成的平面,指向为由Idl经C角转向时 右螺旋前进方向。 dB=kIdlsin a 六3 上美不家返可退此
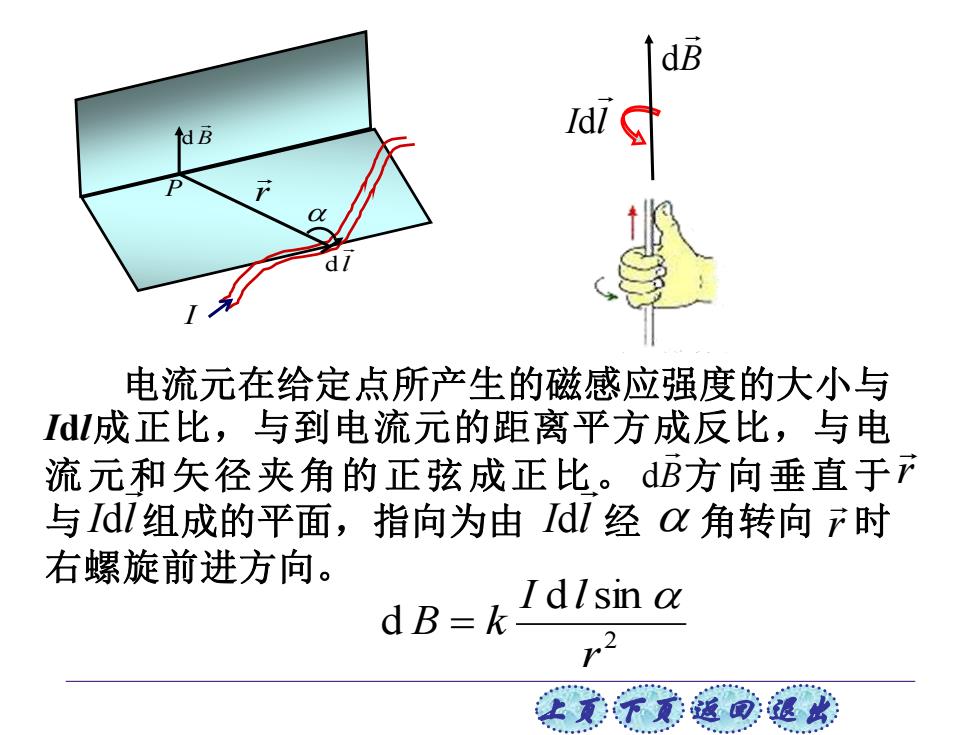
上页 下页 返回 退出 2 d sin d r I l B k = l d I B d r P dB r I l d r 电流元在给定点所产生的磁感应强度的大小与 Idl成正比,与到电流元的距离平方成反比,与电 流元和矢径夹角的正弦成正比。 方向垂直于 与 组成的平面,指向为由 经 角转向 时 右螺旋前进方向。 B d I l d r I l d r I l d B d

而k=/4π故dB= uol dl sin a 4πr2 其中4=4π×10N·A?称为真空中的磁导率。 磁感应强度的矢量式: Biot-Savart定 律的微分形式 dB 4ldl×e 4π Biot-Savart定 律的积分形式 /9 让美下觉返同速
上页 下页 返回 退出 0 2 d d 4π r L L I l e B B r = = 磁感应强度的矢量式: Biot-Savart定 律的微分形式 Biot-Savart定 律的积分形式 其中 ,称为真空中的磁导率。 0 2 d sin d 4π I l B r = 而 k = 4π 故 -7 2 0 4π 10 N A − = 0 2 d d 4π r I l e B r =

二、运动电荷的磁场 电荷运动 形成 电流 激发 激发 磁场 设电流元Id1,横截面积S,单位体积内有n 个定向运动的正电荷,每个电荷电量为g,定向速 度为vo 让美不意返回退此
上页 下页 返回 退出 二、 运动电荷的磁场 电荷运动 形成 电 流 磁 场 设电流元 ,横截面积S,单位体积内有n 个定向运动的正电荷,每个电荷电量为q,定向速 度为v。 I l d

单位时间内通过横截面S的电荷量即为电流强度: I=qnvS 电流元在P点产生的磁感应强度 dB Ho gnvSdl sin 0 4π 2 设电流元内共有N个以速度运动的带电粒子: dN=nSdl 每个带电量为g的粒子以速度v通过电流元所 在位置时,在P点产生的磁感应强度大小为 dB B= Lo gvsin 0 dN 4元 让美觉返司退
上页 下页 返回 退出 单位时间内通过横截面S的电荷量即为电流强度I: 电流元在P点产生的磁感应强度 I = qnvS 设电流元内共有dN个以速度v运动的带电粒子: dN = nS dl 每个带电量为q的粒子以速度v通过电流元所 在位置时,在P点产生的磁感应强度大小为 2 0 sin d 4π d r qv N B B = = 2 0 d sin 4π d r qnvS l B =
矢量式: B= 4qv×e, 4π r2 其方向根据右手螺 旋法则,B垂直少、正 组成的平面。q为正,B 为VX”的方向;q为 负,B与下X产的方向 +g 相反。 V 垂直于纸面向外 垂直于纸面向内
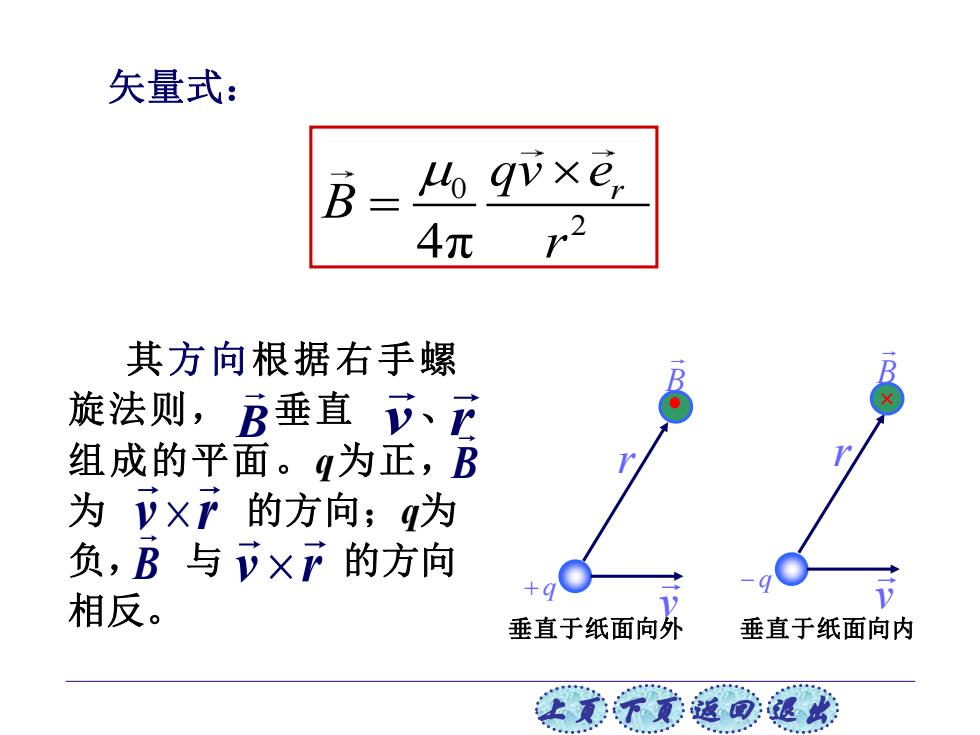
上页 下页 返回 退出 其方向根据右手螺 旋法则, 垂直 、 组成的平面。q为正, 为 的方向;q为 负, 与 的方向 相反。 B v r v B B v r r + q v r B 垂直于纸面向外 r − q v B × 垂直于纸面向内 矢量式: 0 2 4π qv er B r =

三、毕奥一萨伐尔定律的应用 先将载流导体分割成许多电流元Id1 写出电流元Id1在所求点处的磁感应强度,然后按 照磁感应强度的叠加原理求出所有电流元在该点磁 感应强度的矢量和。 实际计算时要首先建立合适的坐标系,求各电流元的 分量式。即电流元产生的磁场方向不同时,应先求出 各分量dB、dB,、dB,然后再对各分量积分。 B=∫dB, B,=∫dB, →B=B,7+B,j+B无 B.=「dB 让美下觉返司速此
上页 下页 返回 退出 B B i B j B k x y z = + + 三、毕奥-萨伐尔定律的应用 写出电流元 在所求点处的磁感应强度,然后按 照磁感应强度的叠加原理求出所有电流元在该点磁 感应强度的矢量和。 先将载流导体分割成许多电流元 实际计算时要首先建立合适的坐标系,求各电流元的 分量式。即电流元产生的磁场方向不同时,应先求出 各分量 d d d B B B x y z 、 、 ,然后再对各分量积分。 I l d I l d = = = z z y y x x B B B B B B d d d
例题8-1 载流长直导线的磁场设有长为L的载流 直导线,其中电流为I。计算距离直导线为a处的P点 的磁感应强度。 解:任取电流元Idl 据毕奥萨伐尔定律,此电 流元在P点磁感应强度为 dB=4oIdixF 4元 3 d方向根据右手螺旋定则 确定。 由于直导线上所有电流元 dB 在该点dB方向相同
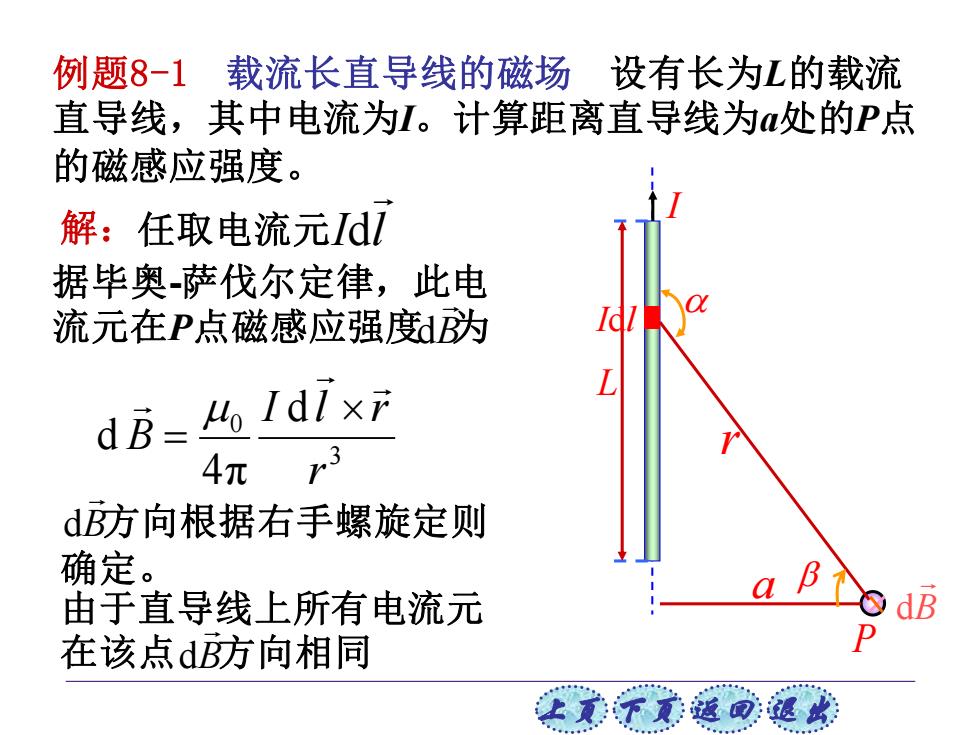
上页 下页 返回 退出 a P 例题8-1 载流长直导线的磁场 设有长为L的载流 直导线,其中电流为I。计算距离直导线为a处的P点 的磁感应强度。 I L I l d r dB r 解:任取电流元 I l d 据毕奥-萨伐尔定律,此电 流元在P点磁感应强度 B 为 d 3 0 d 4π d r I l r B = 方向根据右手螺旋定则 确定。 B d 由于直导线上所有电流元 在该点 B 方向相同 d B d

B=∫dB矢量积分可变为标量积分 B数ma 由几何关系有: sin a=cos B r=asec B 1=atan B dl=asec2BdB B oIdlsin a 4πJL2 凸4 IcospdB 4元a dB (sin B2-sin B.) Ana 让美觉返司退
上页 下页 返回 退出 = L B B d = = L L r I l B B 2 0 d sin 4π d 矢量积分可变为标量积分 由几何关系有: sin = cos r = asec d sec d 2 l = a tan l = a cos d 4π 2 1 0 = a I = L r I l B 2 0 d sin 4π ( ) 2 1 0 sin sin 4π = − a I a P I L I l d r dB r B d
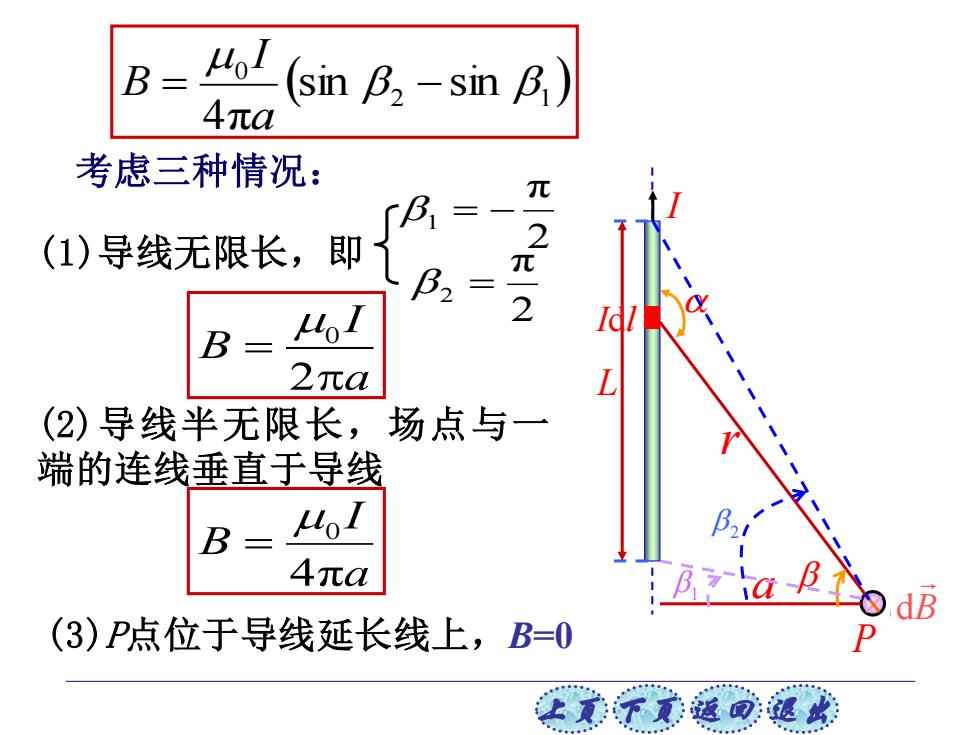
B= 4 4元a (sin B2-sin B) 考虑三种情况: 元 (1)导线无限长,即 2 B2 2 Idl B 41 2πa L (2)导线半无限长,场点与一 端的连线垂直于导线 B 4元a dB (3)P点位于导线延长线上,B=0
上页 下页 返回 退出 考虑三种情况: 0 2 I B a = (1)导线无限长,即 (2)导线半无限长,场点与一 端的连线垂直于导线 a I B 4π 0 = (3)P点位于导线延长线上,B=0 ( ) 2 1 0 sin sin 4π = − a I B 2 π 1 = − 2 π 2 = a P I L I l d r dB r B d 1 2