
§8-8有磁介质时的安培环路定理磁场强度 一、磁化强度 反映磁介质磁化程度(大小与方向)的物理量。 磁化强度:单位体积内所有分子固有磁矩的 矢量和∑m加上附加磁矩的矢量和∑△m子,称 为磁化强度,用M表示。 均匀磁化 M=∑mr+∑AmT △V 非均匀磁化 M lim ∑m分子+∑△m分于 △V→0 △V 磁化强度的单位: A/m 让意不意适回退收
上页 下页 返回 退出 一、磁化强度 反映磁介质磁化程度(大小与方向)的物理量。 均匀磁化 非均匀磁化 V m m M + = 分子 分子 V m m M V + = → 分子 分子 0 lim §8-8 有磁介质时的安培环路定理磁场强度 磁化强度:单位体积内所有分子固有磁矩的 矢量和 加上附加磁矩的矢量和 ,称 为磁化强度,用 M 表示。 m分子 m分子 磁化强度的单位: A/m

注意:对顺磁质,∑i可以忽略; 对抗磁质,∑m=0,对于真空,M=0。 外磁场为零,磁化强度为零。 外磁场不为零: 顺磁质 M、B同向 抗磁质 M、B反向 让美下觉返同速
上页 下页 返回 退出 注意:对顺磁质, 可以忽略; 对抗磁质, ,对于真空, 。 m分子 m分子 = 0 M = 0 外磁场为零,磁化强度为零。 外磁场不为零: 顺磁质 抗磁质 M、B0 同向 M、B0 反向
磁化电流 对于各向同性的均匀介质,在匀强磁场中被磁 化后,各分子电流平面转到与磁场的方向垂直。 介质内部任一点总有两个方向相反的分子电流通过, 各分子电流相互抵消,而在介质表面,各分子电流 相互叠加,在磁化圆柱的表面出现一层电流,好象 一个载流螺线管,称为磁化面电流(或安培表面电 流)。 磁化电流 00000/ 00000 00000 8对 正贰子元道同退此
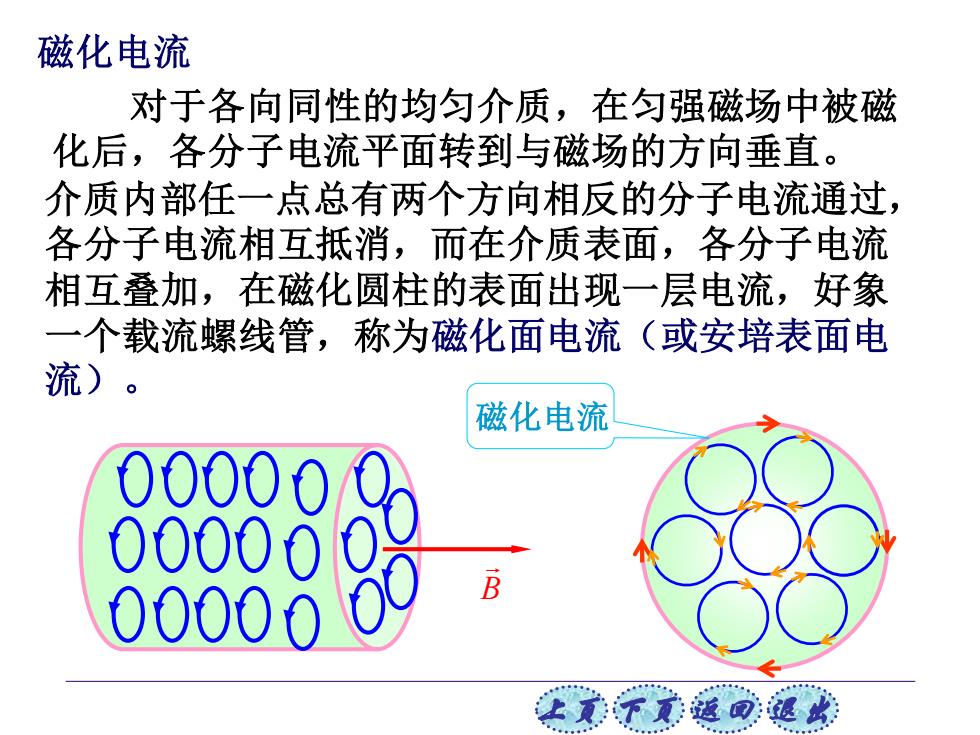
上页 下页 返回 退出 磁化电流 对于各向同性的均匀介质,在匀强磁场中被磁 化后,各分子电流平面转到与磁场的方向垂直。 磁化电流 B 介质内部任一点总有两个方向相反的分子电流通过, 各分子电流相互抵消,而在介质表面,各分子电流 相互叠加,在磁化圆柱的表面出现一层电流,好象 一个载流螺线管,称为磁化面电流(或安培表面电 流)
磁化电流 00000 00000 00000 B 让美下觉返司速此
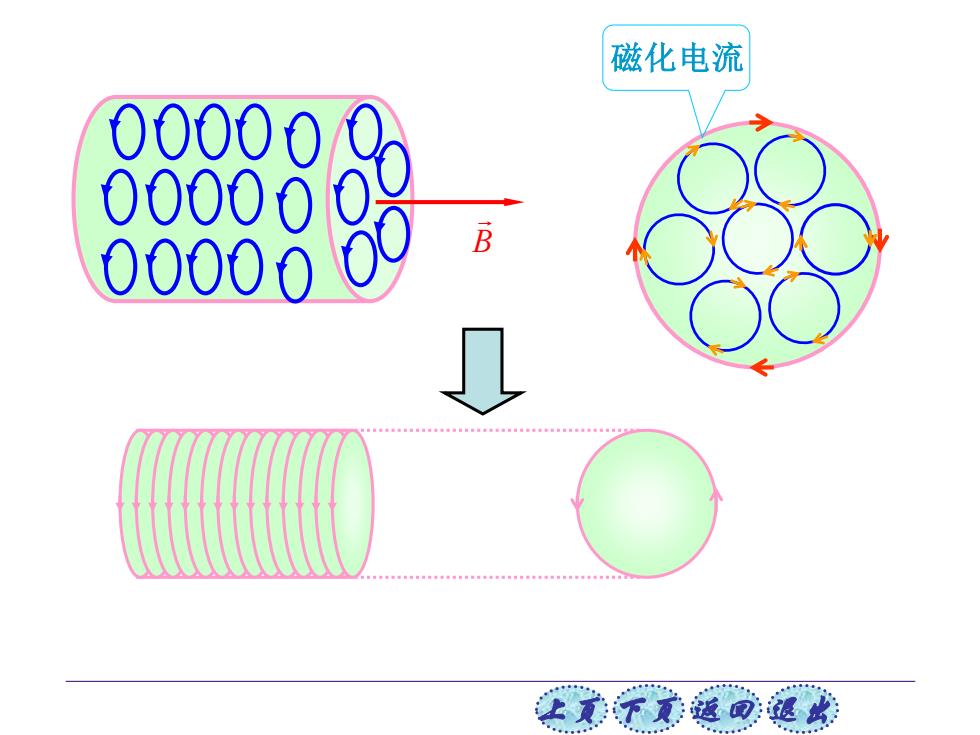
上页 下页 返回 退出 磁化电流 B 磁化面电流
M 8 设介质表面沿轴线方向单位长度上的磁化电 流为.(面磁化电流密度),则长为l的一段介 质上的磁化电流强度s为 Is=al 总磁矩∑m分子=1·S=&,S >M=∑m分于 aSt -as △V SI 让美子元返司退此
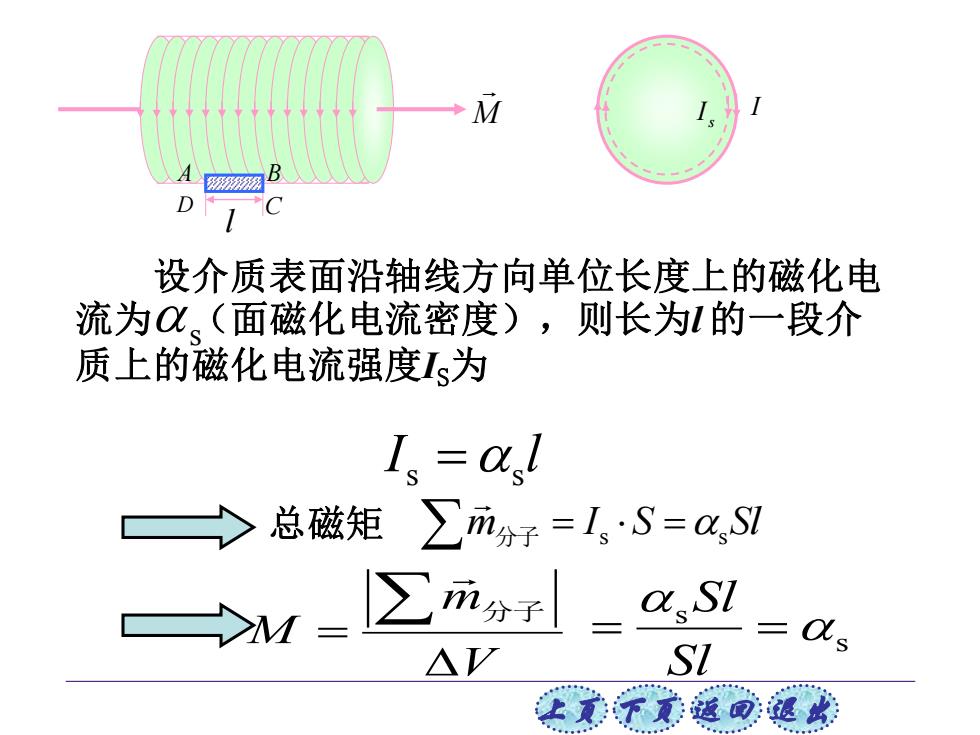
上页 下页 返回 退出 I l s =s m I S Sl s =s 分子 = V m M = 分子 s s = = Sl Sl M A B D C l s I I 设介质表面沿轴线方向单位长度上的磁化电 流为 (面磁化电流密度),则长为l 的一段介 质上的磁化电流强度IS为 s 总磁矩
D 取一长方形闭合回路ABCD,AB边在磁介质 内部,平行与柱体轴线,长度为L,而BC、AD两 边则垂直于柱面。柱外各点M等于零,内部则 平行于AB边,M对整个回路积分 Md7-M.dI=M.AB=MI 因为M=a所以fM.d1=al=1 磁化强度对闭合回路的线积分等于通过回路 所包围的面积内的总磁化电流。 让美下觉返司速此
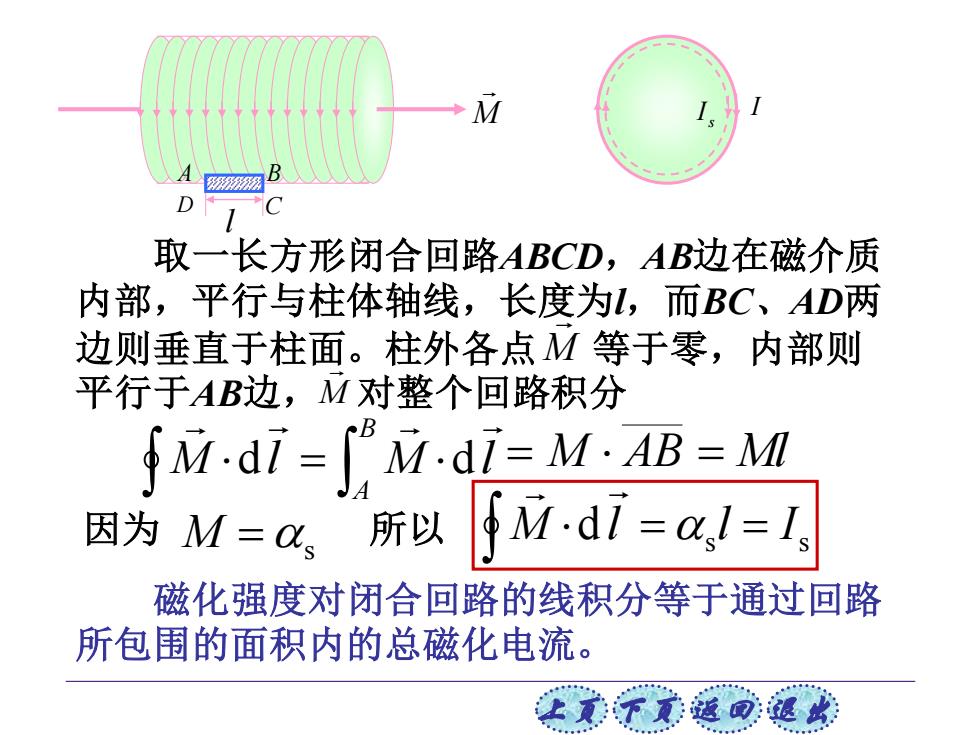
上页 下页 返回 退出 = B A M l M l d d = M AB = Ml M =s s s M dl = l = I 磁化强度对闭合回路的线积分等于通过回路 所包围的面积内的总磁化电流。 取一长方形闭合回路ABCD,AB边在磁介质 内部,平行与柱体轴线,长度为l,而BC、AD两 边则垂直于柱面。柱外各点 等于零,内部则 平行于AB边, 对整个回路积分 M M 因为 所以 M A B D C l s I I

二、有磁介质时的安培环路定理 磁场强度 无磁介质时安培环路定理 fB。df=4∑1。 有磁介质时∮B.di=4(∑I+I,) 因为1=∮M·d 所以∮B.d亚=4(∑I+fM·d) 或 f(五-业=∑1 女贰子意通返回退此
上页 下页 返回 退出 二、 有磁介质时的安培环路定理 = (L内) L B l I 0 d 0 0 无磁介质时安培环路定理 有磁介质时 d ( ) = 0 + s B l I I I M l s = d d ( d ) 0 B l = I + M l − M l =I B ( ) d 0 或 磁场强度 因为 所以
定义磁场强度: H= B-M 40 因为 f(位-M-∑1 有磁介质时的 ∮i.d=∑I 安培环路定理 磁介质中的安培环路定理:磁场强度沿任 意闭合路径的线积分等于穿过该路径的所有传导电 流的代数和,而与磁化电流无关。 表明:磁场强度矢量的环流和传导电流I有关, 而在形式上与磁介质的磁性无关。其单位在国际单位 制中是A/m。 让美下觉返司速此
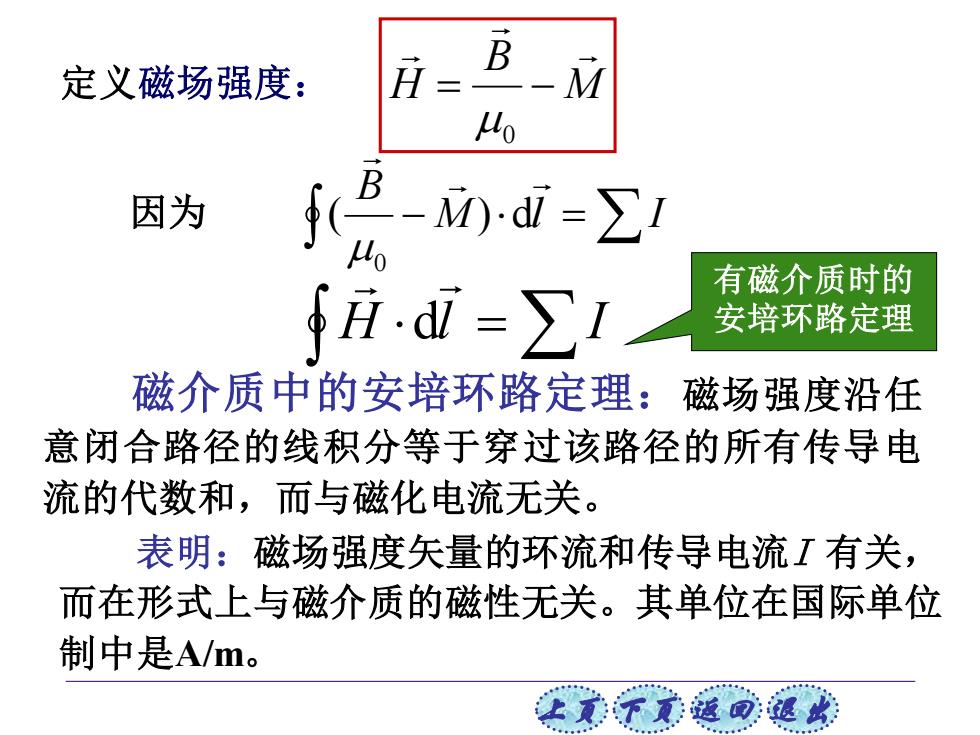
上页 下页 返回 退出 定义磁场强度: M B H = − 0 表明:磁场强度矢量的环流和传导电流I 有关, 而在形式上与磁介质的磁性无关。其单位在国际单位 制中是A/m。 磁介质中的安培环路定理:磁场强度沿任 意闭合路径的线积分等于穿过该路径的所有传导电 流的代数和,而与磁化电流无关。 有磁介质时的 安培环路定理 − M l = I B ( ) d 0 H l = I d 因为

3-M 此式说明了介质中任一点磁场强度、 磁感应强度、磁化强度之间的普遍 关系,不论介质是否均匀。 实验证明:对于各向同性的介质,在磁介质 中任意一点磁化强度和磁场强度成正比。 M 定义介质磁化率飞m= 式中Xm只与磁介质的性质有关,称为磁介质的磁 化率,是一个纯数。如果磁介质是均匀的,它是 一个常量;如果磁介质是不均匀的,它是空间位 置的函数。 Zm>0 顺磁质 2m<0 抗磁质 上美不意返回退必
上页 下页 返回 退出 M B H = − 0 实验证明:对于各向同性的介质,在磁介质 中任意一点磁化强度和磁场强度成正比。 式中 只与磁介质的性质有关,称为磁介质的磁 化率,是一个纯数。如果磁介质是均匀的,它是 一个常量;如果磁介质是不均匀的,它是空间位 置的函数。 m 此式说明了介质中任一点磁场强度、 磁感应强度、磁化强度之间的普遍 关系,不论介质是否均匀。 m 0 顺磁质 m 0 抗磁质 定义介质磁化率 H M m =

B=4,雨+4所 →B=4,(+Xm) M ZnH 磁导 令4,=1+Xn B=44i=iǖ 相对 磁导 真空:M=0, 4=1,Xm=0 值得注意:是为研究介质中的磁场提供方便而 不是反映磁场性质的基本物理量,才是反映磁场性 质的基本物理量。 让美下觉返司速此
上页 下页 返回 退出 B H M = 0 + 0 M H = m 令r =1+ m B H (1 ) = 0 + m B H H = 0 r = 相对 磁导 率 磁导 率 值得注意: 是为研究介质中的磁场提供方便而 不是反映磁场性质的基本物理量, 才是反映磁场性 质的基本物理量。 H B 真空: M = 0, r =1, m = 0