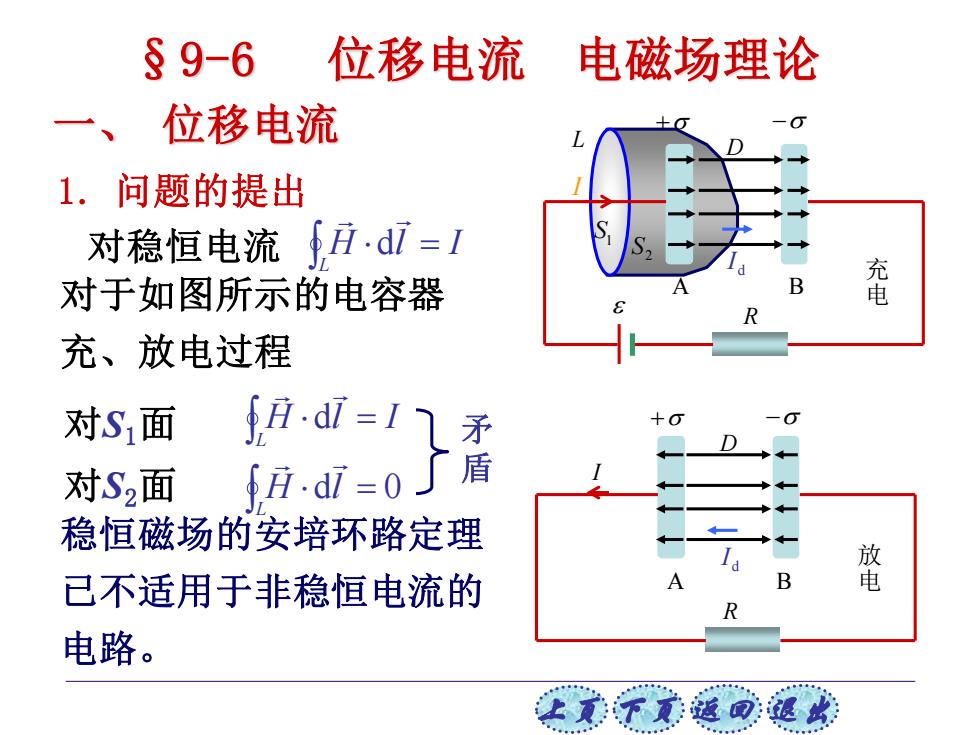
§9-6 位移电流 电磁场理论 一、 位移电流 1.问题的提出 对稳恒电流 H.d7=1 对于如图所示的电容器 鼋 充、放电过程 对S面 一】 对S2面 稳恒磁场的安培环路定理 己不适用于非稳恒电流的 电路。 让美下觉返同速
上页 下页 返回 退出 §9-6 位移电流 电磁场理论 一、 位移电流 1. 问题的提出 = L H l I 对稳恒电流 d 对S1面 = L H l I d 对S2面 = L H dl 0 矛 盾 稳恒磁场的安培环路定理 已不适用于非稳恒电流的 电路。 2 S S1 L I A B R + − D d I A B I R + − D d I 充 电 放 电 对于如图所示的电容器 充、放电过程

位移电流的提出 产生上述矛盾的原因在于非稳定情况下电流不再 连续。电流在极板处出现中断,但极板上的电荷q、 电荷面密度σ、其间的电位移D、通过整个截面的电 位移通量平D=SD都随时间变化。 设平行板电容器极板面积为S,极板上电荷面密 度σ。充、放电过程的任一瞬间 1=sdo D=0 dt 则 I=sdo =sdD dt dt ,又等 上式表明,导线中的电流等于极板上的sd 于极板间的sdD
上页 下页 返回 退出 位移电流的提出 产生上述矛盾的原因在于非稳定情况下电流不再 连续。电流在极板处出现中断,但极板上的电荷q、 电荷面密度σ、其间的电位移D、通过整个截面的电 位移通量ΨD=SD都随时间变化。 设平行板电容器极板面积为S,极板上电荷面密 度σ。充、放电过程的任一瞬间 t I S d d = D = t D S t I S d d d d = = 上式表明,导线中的电流等于极板上的 ,又等 于极板间的 。 t S d d t D S d d 则
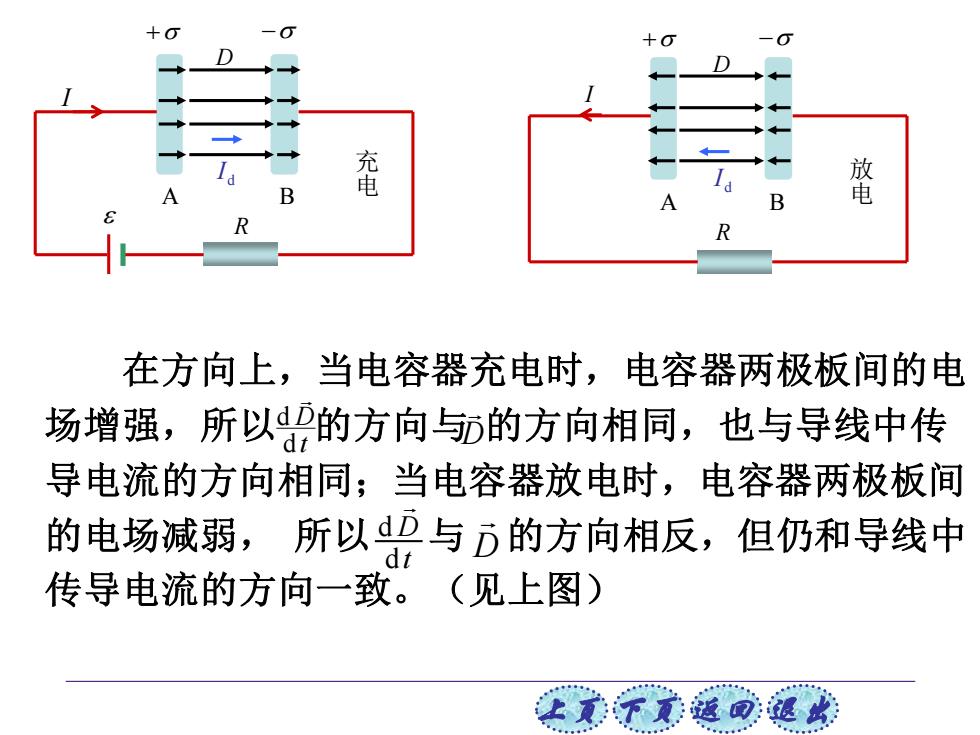
+O B R 在方向上,当电容器充电时,电容器两极板间的电 场增强,所以的方向与的方向相同,也与导线中传 导电流的方向相同;当电容器放电时,电容器两极板间 的电场减弱,所以2与D的方向相反,但仍和导线中 传导电流的方向一致。(见上图) 让美下觉返司速此
上页 下页 返回 退出 在方向上,当电容器充电时,电容器两极板间的电 场增强,所以 的方向与 的方向相同,也与导线中传 导电流的方向相同;当电容器放电时,电容器两极板间 的电场减弱, 所以 与 的方向相反,但仍和导线中 传导电流的方向一致。(见上图) t D d d t D d d D D I A B R + − D d I A B I R + − D d I 充 电 放 电

麦克斯韦认为,可以把电位移通量对时间的变化 率看作一种电流,称为位移电流。 dD 1=S dΨD 位移电流密度为 dD dt dt 电场中某一点位移电流密度矢量等于该点电位移 矢量对时间的变化率;通过电场中某一截面的位移 电流1等于通过该截面电位移通量Ψ对时间的变化 率,即
上页 下页 返回 退出 麦克斯韦认为,可以把电位移通量对时间的变化 率看作一种电流,称为位移电流。 t t D I S d d d d D d = = t D S t j d d d 1 d D d = = 电场中某一点位移电流密度矢量 等于该点电位移 矢量对时间的变化率;通过电场中某一截面的位移 电流 等于通过该截面电位移通量 对时间的变化 率,即 d j d I 位移电流密度为

令传导电流和位移电流相加的合电流I=+I。在 有电容器的电路中,电容器极板表面被中断的传导 电流I,可以由位移电流I继续下去,从而构成了电 流的连续性。 非稳定电流的安培环路定理 在磁场中H沿任一闭合回路的线积分,在数值上 等于穿过以该闭合回路为边线的任意曲面的全电流。 即 f-d-∑0+,)jads+r80a 将上式用于前面的电路取S,面的情况,则 让美觉返司退
上页 下页 返回 退出 令传导电流和位移电流相加的合电流It =I+Id。在 有电容器的电路中,电容器极板表面被中断的传导 电流I,可以由位移电流Id继续下去,从而构成了电 流的连续性。 非稳定电流的安培环路定理 在磁场中H沿任一闭合回路的线积分,在数值上 等于穿过以该闭合回路为边线的任意曲面的全电流。 即 ( ) = + = + S t D H l I I j S d d d d 将上式用于前面的电路取S2面的情况,则

∮i.dl=1 d平 dt →f= dt dt 解决了前面的矛盾之处。 由此可见,位移电流的引入,揭示了电场和磁场 内在的联系和依存关系,反映了自然现象的对称性。 电磁感应定律说明变化的磁场产生祸旋电场,位移电 流的论点说明变化的电场产生涡旋磁场,这两种变化 的场永远互相联系着,形成统一的电磁场
上页 下页 返回 退出 D d d d d H l I t = = D d d d d q I t t = = H l = I d 解决了前面的矛盾之处。 由此可见,位移电流的引入,揭示了电场和磁场 内在的联系和依存关系,反映了自然现象的对称性。 电磁感应定律说明变化的磁场产生涡旋电场,位移电 流的论点说明变化的电场产生涡旋磁场,这两种变化 的场永远互相联系着,形成统一的电磁场

麦克斯韦提出的位移电流概念已经为无线电波的 发现及其广泛的实际应用所证实。 通常导体中的电流主要是传导电流,位移电流可 以不计,电介质中的电流主要是位移电流,传导电流 可以不计。 位移电流与传导电流的关系 (1)位移电流与传导电流在产生磁效应上是等效的。 (2)产生的原因不同:传导电流是由自由电荷运动 引起的,而位移电流本质上是变化的电场。 (3)通过导体时的效果不同:传导电流通过导体时 产生焦耳热,而位移电流不产生焦耳热。 王觉不元菠面:退收
上页 下页 返回 退出 麦克斯韦提出的位移电流概念已经为无线电波的 发现及其广泛的实际应用所证实。 通常导体中的电流主要是传导电流,位移电流可 以不计,电介质中的电流主要是位移电流,传导电流 可以不计。 位移电流与传导电流的关系 (1) 位移电流与传导电流在产生磁效应上是等效的。 (2) 产生的原因不同:传导电流是由自由电荷运动 引起的,而位移电流本质上是变化的电场。 (3)通过导体时的效果不同:传导电流通过导体时 产生焦耳热,而位移电流不产生焦耳热

例9-13半径为R=0.1m的两块圆板构成平行板电容器, 由圆板中心处引入两根长直导线给电容器匀速充电,使 电容器两板间电场的变化率为dE/d仁1013V(ms)。求电 容器两板间的位移电流,并计算电容器内离两板中心连 线处<R)的磁感应强度B和R处的BR。 解:电容器两极板间的位移电流为 E dE =2.8A dt 电容器两极板间的心R处各点磁感应强度为B,应用安 培环路定理
上页 下页 返回 退出 例9-13 半径为R=0.1m的两块圆板构成平行板电容器, 由圆板中心处引入两根长直导线给电容器匀速充电,使 电容器两板间电场的变化率为dE/dt=1013 V/(m·s) 。求电 容器两板间的位移电流,并计算电容器内离两板中心连 线处r(r<R)的磁感应强度Br和R处的BR 。 解:电容器两极板间的位移电流为 电容器两极板间的r<R处各点磁感应强度为Br,应用安 培环路定理 R E r 2.8A d d π d d d d 0 D 2 d = = = = t E R t D S t Ψ I

手i-d-1%2r-∬0as de 故 B.= 1 2 dt 当r=R B= dE =5.6×10-6T 2 上面所计算得到的电场是全电流激发的总磁场。 让美觉返司退
上页 下页 返回 退出 = = S t D H l B r r 2π d 1 d 0 t E B r r d d 2 0 0 = 当 r = R 5.6 10 T d d 2 0 0 −6 = = t E Br R 上面所计算得到的电场是全电流激发的总磁场。 R E r 2 0 0 d d d π d d E E S R t t = = 故
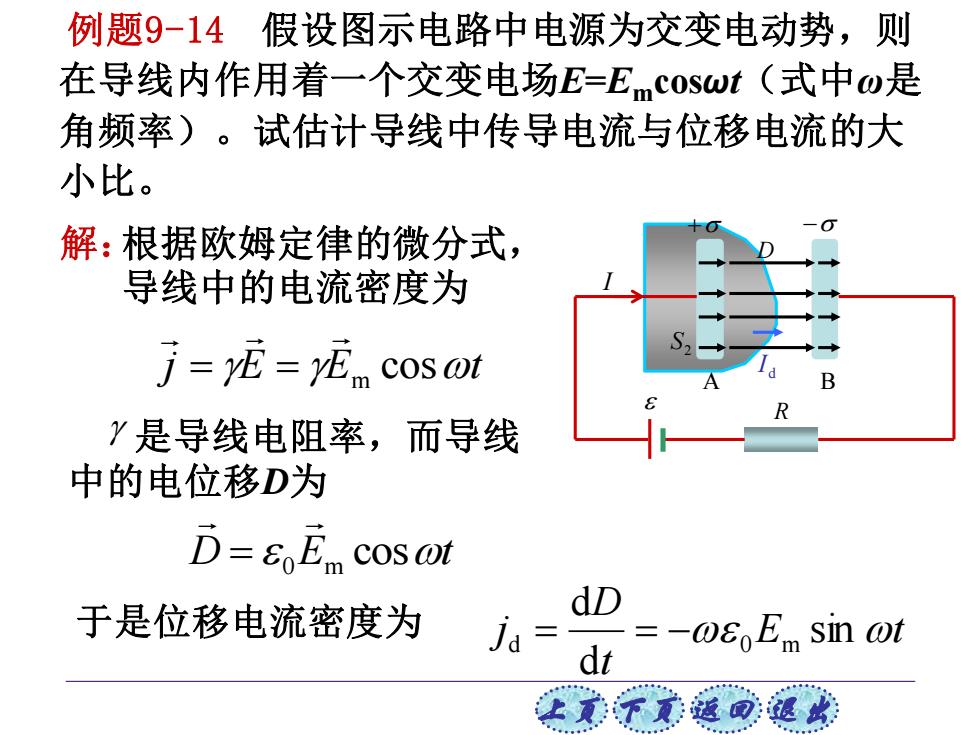
例题9-14假设图示电路中电源为交变电动势,则 在导线内作用着一个交变电场E-Emcoswt(式中w是 角频率)。试估计导线中传导电流与位移电流的大 小比。 解:根据欧姆定律的微分式, 导线中的电流密度为 j=yE=yE cos ot Y是导线电阻率,而导线 中的电位移D为 D=E0Em cos cot 于是位移电流密度为 dD jd= dr =-0oEm sin ot 让贰不元通回退欢
上页 下页 返回 退出 例题9-14 假设图示电路中电源为交变电动势,则 在导线内作用着一个交变电场E=Emcosωt(式中ω是 角频率)。试估计导线中传导电流与位移电流的大 小比。 2 S I A B R + − D d I 解: 于是位移电流密度为 j E E cost m = = 是导线电阻率,而导线 中的电位移D为 D E cost 0 m = E t t D j sin d d d = = − 0 m 根据欧姆定律的微分式, 导线中的电流密度为